poemas de cesar Brandon (videos)

"A Destiempo"

 

poema de Mamá

poema  Después de la señal

¡A UN AÑO LUZ DE CERCANÍA! (de César Brandon) | Mateo Sánchez

Uno y Cero Poema de césar brandon

 

Uno y Cero Poema de césar brandon 

Uno y Cero

Poema de césar brandon

Vino de Guinea Ecuatorial para triunfar con su poesía | Audiciones 5 | Got Talent España 2018

Uno no quería contar con nadie
y Uno no entendía porque era impar
si antes de él había alguien
Uno no quería contar con nadie

y uno sentía que después de él estaba el infinito
y a Uno ese epíteto le daba miedo
así que Uno muerto de pavor se fijó en Cero
y cuando Uno vio a Cero pensó que Cero era el número más bonito que había visto

y que aun viniendo antes que él era entero
pensó que en Cero había encontrado el amor verdadero
en Cero había encontrado a su par
así que decidió ser sincero con Cero

y decirle que aunque era un Cero a la izquierda
sería el Cero que daría valor y sentido a su vida
eso de ser el primero ya no le iba
así que le dio a Cero la gran bienvenida

juntos eran pura alegría y se completaban
Uno tenía cero tolerancia al alcohol
pero con Cero se podía tomar una cerveza cero por su aniversario
que para eso tenía que inventarse una fecha cero en el calendario

pero era algo cerrado y le costaba representar textos
pero junto a Uno hacían el perfecto código binario
y eran los dígitos del barrio
y procesaban el amor a diario

pero Uno no sabe lo que tiene hasta que lo pierde
así que Uno perdió a Cero
y para cuando Uno se dio cuenta
Cero ya contaba de la mano con Menos Uno

que a pesar de ser algo negativo la trataba como a una reina
a Cero le gustaba que Menos Uno fuera original
tener un hueco en Menos Uno
un guión con el que podían jugar

a Cero le gustaba que menos uno no fuera uno más
que Menos Uno no fuese ordinal
que fuese justamente competitivo
y que cuando jugasen al uno

Menos Uno no le dejase ganar
Cero sentía que a diferencia de Uno
Menos Uno le trataba como a un número de verdad
y Menos Uno no ponía peros ni pretendía darle valor a Cero
poniendo comas entre ellos

Menos Uno no tenía complejos
y cuando hacían el amor
a Menos Uno le encantaba estar bajo Cero
y Uno una vez más volvió a quedarse solo
separado como una unidad

sin Cero su vida se consumía como una vela
sin Cero el tiempo en él hacía mella
y Uno empezó a contar
pero sin Cero

se olvidó de los pesos de Cero
del sexo con Cero
de los celos de Cero
y empezó a contar pero sin Cero

Uno se olvidó de Cero y le dijo adiós
Uno se olvidó de Cero y tal vez del amor
y empezó a contar hacia lo que más miedo le daba
hasta el infinito o tal vez solo hasta Dos.

Acróstico

              Mirar soñando despierto

Al ver dos líneas trazadas

Te refleja como ciertos

Espacios que son del alma;

Mar de infinitos destellos

Acotados por las blancas

Trazas que dejan abiertos

Imposibles movimientos

Capaces de abrir las marcas

Alcanzadas por expertos

Sabios de todos los tiempos

Y soñando lograremos

Penetrar en las esencias

Ocultas de los extremos

Esquivos de las conciencias,

Sabiendo que toda ciencia

Incluye cuando queremos

Algo de amor y cadencia    

José Antonio Hervás

poesía EL ALGEBRISTA

 EL ALGEBRISTA

  

Algebrista te volviste

refinado hasta la esencia

oligarca de la ciencia

matemático bacán.

Hoy mirás a los que sudan

en las otras disciplinas

como dama a pobres minas

que laburan por el pan.

¿Te acordás que en otros tiempos

sin mayores pretensiones

mendigabas soluciones

a una mísera ecuación?

Hoy la vas de riguroso

revisás los postulados

y junás por todos lados

la más vil definición.

Pero no engrupís a nadie

y es inútil que te embales

con anillos, con ideales

y con álgebras de Boole.

Todos saben que hace poco

resolviste hasta matrices

y rastreabas las raíces

con el método de Sturm.

Pero puede que algún día

con las vueltas de la vida

tanta cáscara aburrida

te llegue a cansar al fin.

Y añores tal vez el día

que sin álgebras abstractas

y con dos cifras exactas

te sentías tan feliz.   

  

  Enzo R. Gentile

POEMA EL LADRÓN DE NARANJAS

 

EL LADRÓN DE NARANJAS Un ladrón un cesto de naranjas del mercado robó y por entre los huertos escapó; al saltar una valla, la mitad más media perdió; perseguido por un perro, la mitad menos media abandonó; tropezó en una cuerda, la mitad más media desparramó; en su guarida, dos docenas guardó. Vosotros, los que buscáis la sabiduría, decídnos: ¿cuántas naranjas robó el ladrón? Córdoba: Escuela del Califa

 

 El Hombre que Calculaba

DESCARGA LIBRO

El hombre que calculaba, es un libro con la peculiaridad de ser tomada como novela y un libro de indagaciones y dificultades matemáticas. Su autor expreso que con esta novela intentaba contribuir a la popularización de las matemáticas, presentándolas incorporadas a situaciones diarias y cruzadas por muchísimas variables, tales como la moral e historia.

Información general del libro

El personaje principal, Beremiz, fue desarrollado como un personaje sencillo, lo que nos relaciona de manera inmediata a este personaje complaciente, copartícipe, demostrativo, involucrado en resolver los problemas de los demás y muy sensible a la poesía. Esta novela enlaza lo cotidiano y útil con las matemáticas, a través de historias y leyendas, haciéndolo llevadero y ameno, mostrándonos de una manera lógica y simple, la manera de resolver los problemas que se van describiendo.

Una particularidad de este libro es que el narrador está presente formando parte del relato, aunque no es el protagonista de la novela. Además podemos ver a lo largo de la obra la creencia de cada personaje por la religión musulmana.

En este apartado se presentan elementos de interés sobre El hombre que calculaba, escritor, año de publicación, género literario y su idioma de origen. Esto nos permitirá ubicarnos no solo geográficamente el cuento sino en que época fue concebida y algunos aspectos particulares del autor del mismo.

Autor

El escritor fue Julio Cesar de Mello Souza, mejor conocido con el seudónimo de Malba Tahan. Logró escribir más de 50 libros bajo este nombre, empleando historias orientales para ir enseñando sobre las matemáticas. La obra de El hombre que calculaba, fue su libro más famoso y estuvo en el reciente en la lista de los libros más vendidos de la historia.

Durante la primera mitad del siglo XX, los escritores brasileros se interesaron en la cultura árabe, gracias al profesor Julio Cesar de Mello e Souza. Este libro contienen aventuras en paisajes árabes junto con problemas y soluciones de algebra y aritmética.

Su obra más famosa, El hombre que calculaba o “O Homem que calculava” en su idioma original el portugués, enseña todas las historias y situaciones en escenarios árabes muy típicos a la par de impresionantes soluciones a problemas y planteamientos de algebra y aritmética. Esta obra ya llego a su edición número 63 de la cada de publicaciones Record de Brasil y según los conocedores sigue contando.

Esta novela ha logrado la hazaña de aparecer aun después de 63 ediciones, en el quinto lugar en la lista de los libros u obras más vendidas de acuerdo a lo publicado en el periódico O Globo, en mayo del año 2004.

Julio Cesar o mejor conocido como Malba Tahan, ha escrito en total 103 libros, lo que incluye textos de ciencia y ficción, novelas escolares y libros científicos. Ha logrado vender más de 2,6 millones de copias a nivel mundial.

Resumen por capítulos de El hombre que calculaba

VIDEOS DE APOYO PARA LA RESOLUCIÓN DE ECUACIONES DE PRIMGRADO

 

VIDEOS DE APOYO PARA LA RESOLUCIÓN DE ECUACIONES DE PRIMGRADO

El Diablo de los números

 

 El Diablo de los números 

(DESCARGAR LIBRO)

Resumen (Primera parte)

El libro  El Diablo de los números fue bien recibido por los críticos que reconocieron su descripción de las matemáticas y elogiaron su simplicidad. Su rico uso de términos matemáticos y su descripción creativa de conceptos lo convierten en un libro de recomendaciones para niños y adultos que le temen a las matemáticas.

Argumento

Robert es un joven que sufre de ansiedad matemática debido al aburrimiento en la escuela. Ha experimentado sueños repetidos, incluido caerse por un tobogán sin fin o ser devorado por un pez gigante, pero estos sueños fueron interrumpidos durante la noche por un pequeño animal que se llamaba a sí mismo un “demonio digital”. A pesar de la gran cantidad de personas, Robert no sabía su nombre real Teplotaxl hasta entonces, y no lo conocía de esa manera. En el proceso de doce sueños, el demonio digital le enseñó a Robert los principios de las matemáticas.

En la primera noche, el diablo apareció en un mundo enorme con Robert y lo presentó al número 1. A la noche siguiente, el diablo apareció en un bosque de árboles compuestos por “unos”, explicó la necesidad del número cero, números negativos e introdujo el salto, que es un término virtual que se refiere a exponenciación. En la tercera noche, el diablo llevó a Robert a una cueva y le reveló cómo los números primos solo se pueden dividir por sí mismos y uno sin resto. Más tarde, en la cuarta noche, el diablo le enseñó a Robert Turnip otra forma de representar las raíz cuadrada, en una playa.

Unas noches más tarde, Robert no pudo encontrar al diablo en su sueño. Hasta la quinta noche, Robert se encontró en el desierto. El diablo le enseñó números triangulares usando cocos. En la 6 noche, el diablo le enseñó a Robert la secuencia de Fibonacci de la naturaleza. El diablo acortó el número, lo llamó número de Bonatschi y contó los conejos marrones y blancos porque se criaron varias veces. Gracias a este sueño, la madre de Robert notó que estaba más interesado en las matemáticas y comenzó a dormirse antes para encontrarse con el diablo.

En la 7 noche, Robert cayó en una habitación blanca y vacía, y el diablo lo llevó al patrón del triángulo de Pascal y la pantalla de matriz triangular. En la octava noche, llevaron a Robert a su escuela. El demonio digital reunió a los compañeros de clase de Robert de muchas maneras y le enseñó el número factorial.

De cierta manera,  cuando Robert soñó que el diablo aparecía a su lado, cayó enfermo. Este le enseñó a Robert sobre los números naturales, las series infinitas. En el comienzo de la décima noche, Robert se encontró en el Polo Norte, donde el diablo le presentó los números irracionales, así como la geometría euclidiana, varios aspectos de vértices (puntos) y aristas (líneas).

Robert ya tenía un verdadero interés por las matemáticas , pero cuestionó su validez, el demonio le presentó el concepto de prueba matemática, y finalmente el diablo le mostró a Robert una cosa complicada. Prueba aritmética básica. En la duodécima noche, Robert y el diablo recibieron una invitación (el nombre del diablo es Teplotaxl) porque el encuentro entre el diablo y Robert terminó y visitaron el infierno.

En el paraíso digital, Robert aprende números imaginarios y botellas de Klein. Viajando por el cielo digital, Teplotaxl presentó a Robert a varios matemáticos famosos como Fibonacci, Bertrand Russell o Gauss. El libro termina con Robert usando su conocimiento matemático recientemente descubierto en su salón de clases.

poesia matemáticas EL CERO, EL UNO Y EL DOS

 

EL CERO, EL UNO Y EL DOS

 

Grandes autores contaron

que en el país de los ceros

el uno y el dos entraron

y desde luego trataron,

de medrar y hacer dinero.

Pronto el uno hizo cosecha,

pues a los ceros honraba

con amistad muy estrecha,

y, dándoles a derecha,

así el valor aumentaba.

Pero el dos tiene otra cuerda:

¡Todo es orgullo maldito!

Y con táctica tan lerda

los ceros pone a la izquierda

y así no medraba un pito.

En suma: el humilde uno

llegó a hacerse millonario

mientras el dos importuno,

por su orgullo cual ninguno

no pasó de perdulario.

Luis Balbuena

POESIA: A LA DIVINA PROPORCIÓN

 

A LA DIVINA PROPORCIÓN

 

A ti, maravillosa disciplina,

media, extrema razón de la hermosura

que claramente acata la clausura

 viva en la malla de tu ley divina.

 

A ti, cárcel feliz de la retina,

áurea sección, celeste cuadratura,

misteriosa fontana de mesura

que el universo armónico origina.

 

A ti, mar de los sueños angulares,

flor de las cinco formas regulares,

dodecaedro azul, arco sonoro.

 

Luces por alas un compás ardiente.

Tu canto es una esfera transparente.

A ti, divina proporción de oro.

 

Rafael Alberti Poemas del destierro

 

SEGUNDOS AÑOS 26/10/2020 TEMA: Múltiples representaciones algebraicas del perímetro

SEGUNDOS AÑOS

26/10/2020

TEMA: Múltiples representaciones algebraicas del perímetro

 Aprendizaje esperado: Formula expresiones de primer grado para representar propiedades (perímetros y áreas) de figuras geométricas y verifica su equivalencia en expresiones, tanto algebraica como geométricamente (análisis de las figuras).

 

Énfasis: Formular conjeturas y validar las múltiples representaciones algebraicas del perímetro de las figuras y establecer su equivalencia.

 

 

¿Qué vamos a aprender?

 

Profundizarás en el estudio de las expresiones algebraicas equivalentes que modelan o representan propiedades de las figuras geométricas. En particular, determinarás la medida del perímetro de algunas figuras o superficies.

 

 

¿Qué hacemos?

 

Analiza y responde las siguientes preguntas:

 

1. ¿Qué es el perímetro de una figura?
2. ¿Cómo se calcula?
3. ¿Cómo se determina el perímetro de una figura geométrica?

 

En esta sesión, construirás argumentos para responder estas y muchas otras preguntas que seguramente te has planteado al estudiar temas de matemáticas.

 

Inicia ayudando a Brandon, alumno que estudia segundo de secundaria, a resolver la situación-problema que le asignó su profesor de Matemáticas.

 

La situación-problema dice así:

 

Situación-problema, centro deportivo.

 

Jesús trabaja en la construcción de un centro deportivo, y se están diseñando áreas para la práctica de diferentes deportes, como: frontón, futbol, basquetbol, salto de longitud, entre otros. Para delimitar las áreas y evitar accidentes se decidió colocar malla ciclónica en el perímetro de cada sección.

 

La malla ciclónica es una tela de alambre cuyo tejido tiene diversas formas geométricas, como rombos, cuadrados o rectángulos. Y se usa frecuentemente para delimitar áreas deportivas.

 

Jesús trazó las figuras que representan algunas secciones de las áreas deportivas, anotando el dato de los rollos necesarios para delimitar cada lado de las mismas.  Analiza las figuras y responde algunas preguntas:

 

 

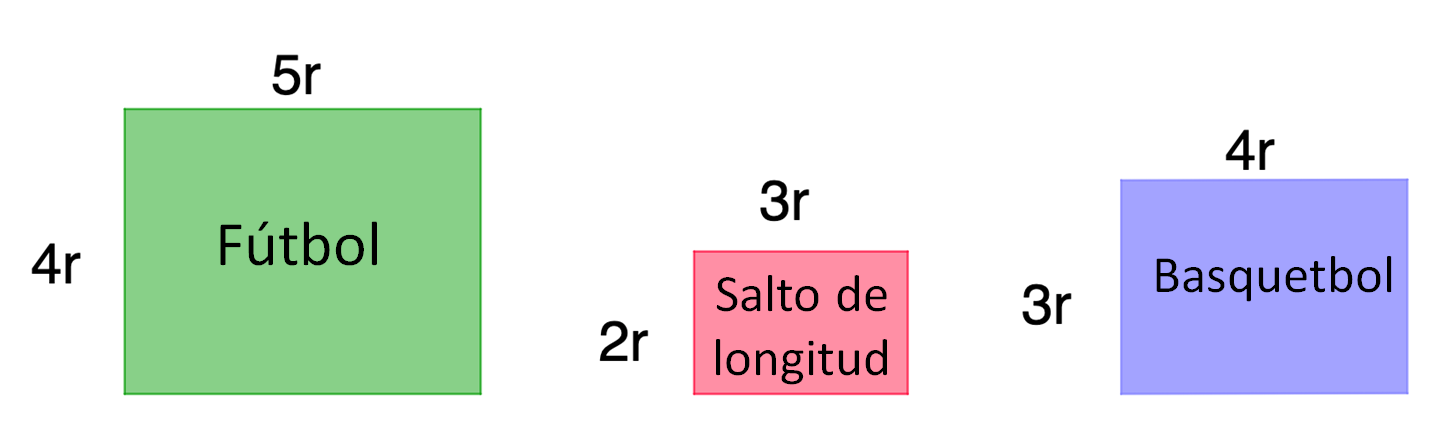
¿Qué sección ocupará mayor cantidad de malla ciclónica?

 

• Futbol
• Salto de longitud
• Basquetbol

 

Como puedes observar en la imagen, cada una de las secciones destinadas para practicar futbol, basquetbol y salto de longitud tiene una forma rectangular. En cada figura de las secciones deportivas se anotó el número de rollos de malla ciclónica para cada lado, donde la literal “r” representa un rollo completo de malla.

 

Si se va a colocar la malla:

 

¿Cuántos rollos de malla se requieren para delimitar el perímetro de cada sección?

 

¿Qué sección ocupará mayor cantidad de malla ciclónica?

 

Para responder la pregunta es necesario conocer cuál es la cantidad de malla ciclónica que se necesita para cada sección.

 

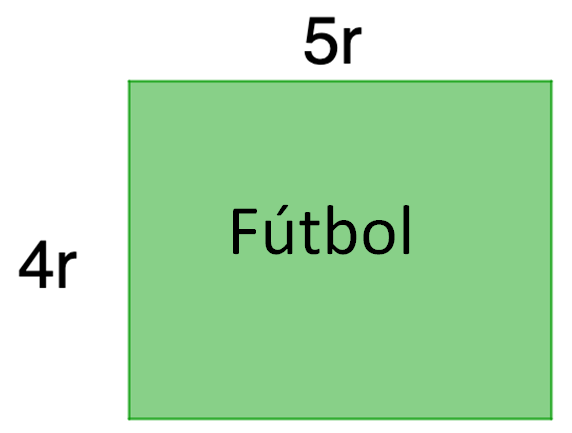
En la imagen, la primera figura rectangular representa la sección destinada como cancha de futbol, y se necesitan 4r de ancho y 5r de largo.  

 

Cada “r” representa un rollo completo de malla ciclónica, entonces “4r” representa 4 rollos completos de malla ciclónica y “5r” representa 5 rollos completos de malla ciclónica.

 

¿Cuál es el perímetro de la sección destinada para practicar futbol?

 

A continuación, analiza las respuestas de Nataly y Fabián sobre el perímetro de la figura.

 

Nataly, una estudiante de secundaria dice que el perímetro de la sección para jugar futbol es:

 

P = 4r + 4r + 5r + 5r.

 

Fabián, su hermano, dice:

 

P = 2(5r) + 2(4r).

 

 

¿Qué razonamiento hay detrás de esas expresiones?

 

Continúa analizando el procedimiento que realizaron Nataly y Fabián para calcular el perímetro.

 

Nataly explicó que se basó en la idea de que el perímetro de cualquier figura se obtiene al sumar la medida de todos sus lados y, como en este caso es un rectángulo, entonces: a + a + b + b determinó que: 

 

P = 4r + 4r + 5r + 5r.

 

Su razonamiento es correcto, además dijo, “puedo comprobar que estoy en lo correcto”. Por lo tanto, explicó que si se realizan las sumas de los sumandos que son iguales, se obtiene la expresión 8r + 10r = 18r, y si finalmente se realiza la suma, el resultado es 18r

 

Fabián explicó, que él sustituyó las medidas del rectángulo en la fórmula del perímetro de esta figura que es:

 

P = 2b + 2a

 

Por lo que, “tenemos dos veces la medida de la base, más dos veces la medida de la altura: P = 2(5r) + 2(4r) Él señaló que:

 

“Si se realizan las multiplicaciones, se obtiene: P = 10r + 8r, al resolver la suma, el perímetro es igual a 18r”

 

 

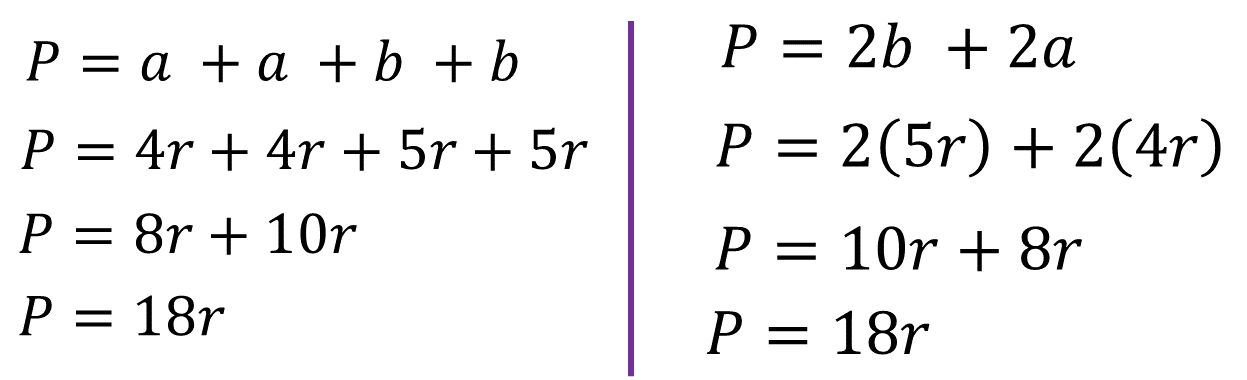
Tanto Nataly como Fabián propusieron expresiones algebraicas que modelan el perímetro de la figura rectangular que representa la sección destinada como cancha de fútbol; y comprobaron que sus expresiones son equivalentes, ya que llegaron al mismo resultado.

 

Es decir, si se escribe la expresión propuesta por Nataly y se iguala con la que propuso Fabián, se tiene:

 

4r + 4r + 5r + 5r = 2(5r) + 2(4r)

 

Si se realizan las operaciones indicadas en cada lado de la igualdad, en el lado izquierdo de la igualdad se suman los términos semejantes y en el lado derecho se multiplica 2 por 5r y se suma con el resultado de la multiplicación 2 por 4r. Ahora la igualdad queda como:

 

18r = 10r + 8r

 

Finalmente, se reducen los términos semejantes en el lado derecho de la igualdad, y queda: 18r = 18r

 

Lo anterior indica que las expresiones algebraicas propuestas por Nataly y Fabián para calcular el perímetro de la cancha de futbol son equivalentes.

 

De esta manera, se sabe que con las expresiones algebraicas equivalentes propuestas por Nataly y Fabián se puede expresar el perímetro con base en la cantidad de rollos de malla ciclónica que se necesitan para la sección de la cancha de futbol.

 

4r + 4r + 5r + 5r = 2(5r) + 2(4r)

 

Entonces, las dos expresiones algebraicas están escritas de manera distinta, pero tienen el mismo valor numérico después de asignar un valor a cada literal y realizar operaciones, son equivalentes.

 

Continúa con la sección que refiere al área de salto de longitud, bajo la explicación de Nataly y Fabián.

 

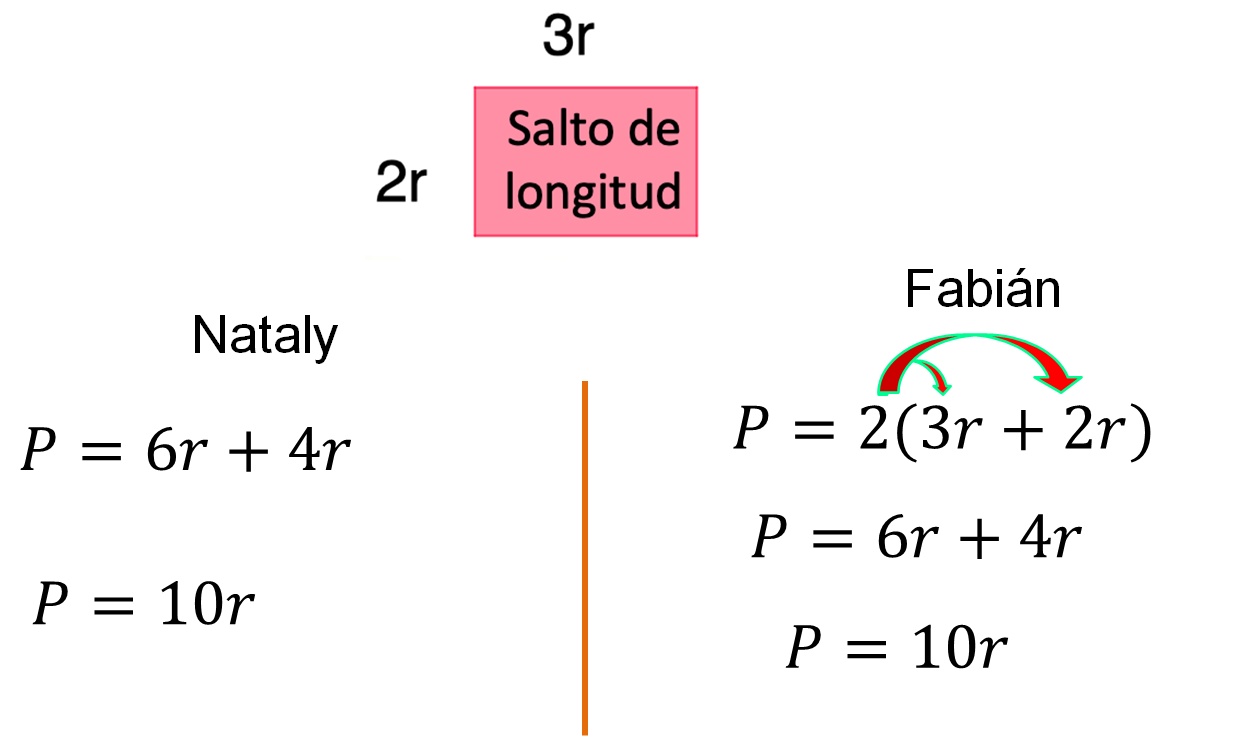
Al observar la sección destinada a la práctica del salto de longitud, se sabe que la medida de la base es 3r y la altura es 2r

 

Nataly establece la igualdad: P = 6r + 4r

Fabián escribe la igualdad: P = 2(3r + 2r)

 

Analiza las expresiones de Nataly y Fabián:

 

¿Estas expresiones pueden ser equivalentes?

 

¿Cómo puedes comprobar si hay o no una relación de equivalencia entre ellas?

 

Nataly dice:

 

“Para obtener el perímetro del rectángulo, consideré sumar dos veces la medida de la base, es decir 3r más 3r, más dos veces la medida de la altura, es decir, 2r más 2r, y obtuve la expresión: P = 6r + 4r”

 

Al resolver las operaciones para simplificar la expresión sumé 6r y 4r, y obtuve que el perímetro es igual a 10r”

 

Fabián explica:

 

“Decidí multiplicar por dos la suma de la medida de la base, que es 3r, más la medida de la altura, que es 2r”, por ello escribí la expresión: P = 2(3r + 2r), y sé que al efectuar la multiplicación su producto es P = 6r + 4r, ya que: 2 por 3r es igual a 6r, y 2 por 2r es igual a 4r

 

Al realizar la suma, 6r más 4r, el perímetro es igual a 10r”

 

 

Con la explicación de Nataly y Fabián:

 

¿Se comprueba que las expresiones son equivalentes? ¿Por qué? 

Escribe tus respuestas y tus dudas.

 

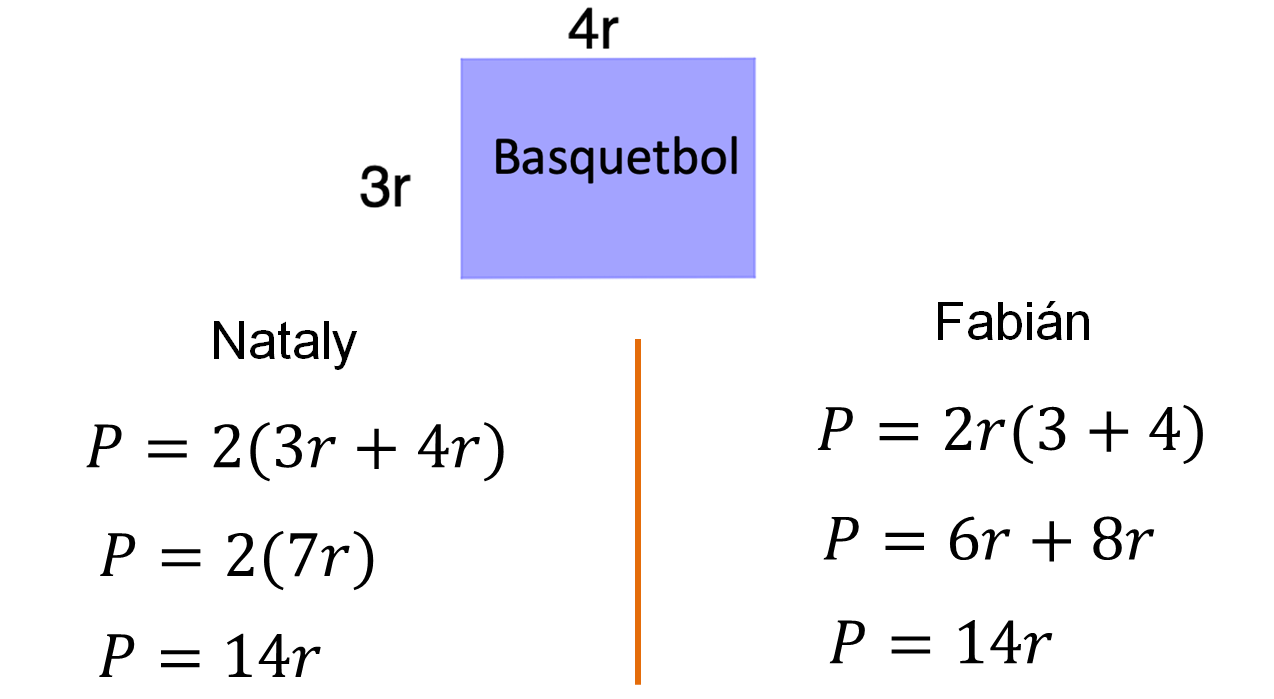
Ahora analiza lo que Nataly y Fabián realizaron para obtener el perímetro de la sección destinada al basquetbol.

 

Al observar la figura que representa la sección para jugar basquetbol en el centro deportivo, se identifica que se trata también de un rectángulo con medidas de “4r” de base y “3r” de alto.

 

Nataly escribió la siguiente expresión algebraica para calcular el perímetro:

 

P = 2(3r + 4r)

 

Por otra parte, Fabián escribió la siguiente expresión algebraica para calcular el perímetro:

 

P = 2r (3+4)

 

¿Consideras que estas dos expresiones algebraicas sean equivalentes?

 

Nataly explicó: “Igualé el perímetro con la multiplicación de dos por la suma de las medidas de la base que es 4r, y la altura 3r, obteniendo que P = 2 (7r). Al realizar la multiplicación obtengo la expresión algebraica para calcular el perímetro de la cancha de basquetbol, la cual es P = 14r”.

 

Fabián dijo que al observar la figura y el dato de las medidas del rectángulo identificó que ambas tienen la misma literal, por lo que igualó el perímetro con la suma de los productos dobles de cada longitud; es decir, P = 2r (3 + 4), al realizar las multiplicaciones se tiene la suma de los productos obtenidos, P = 6r + 8r. Finalmente, se reducen términos semejantes, obteniendo la expresión algebraica P = 14r

 

 

Para entender lo qué significan las expresiones equivalentes, sólo es cuestión de comprender sus representaciones y sus significados para poder establecerlas.

 

Ya resolviste el primer problema. Además, estudiaste una situación en la que calculaste el perímetro de las secciones que serán destinadas a la práctica de un deporte que es de utilidad. Por otro lado, entendiste las expresiones equivalentes.

 

Una forma de saber si dos expresiones son equivalentes consiste en utilizar las propiedades de reducción de términos semejantes y de agrupación.

 

Observa el siguiente ejemplo:

 

4xy + 2xz – 3xy + 5xz – yz = y (x – z) + 7xz

 

Si partes de la expresión algebraica de la izquierda, mediante la reducción de términos semejantes y las propiedades de agrupación, obtendrás la expresión de la derecha.

 

Para lograr lo anterior, se reducen términos semejantes:

 

 

Y luego por las propiedades de agrupación se tiene: “y”, que es factor común por x – z, + 7xz. Por lo tanto: 4xy + 2xz – 3xy + 5xz – yz, es una expresión equivalente de:

 

y (x – z) + 7xz

         

A continuación, revisa otra situación-problema.

 

Judith y Romina son compañeras de clase, su profesora de matemáticas les asignó una tarea y decidieron trabajar juntas para entregar una respuesta consensuada. Observa su tarea y la explicación de los procedimientos que utilizaron, con la finalidad de llegar a un acuerdo.

 

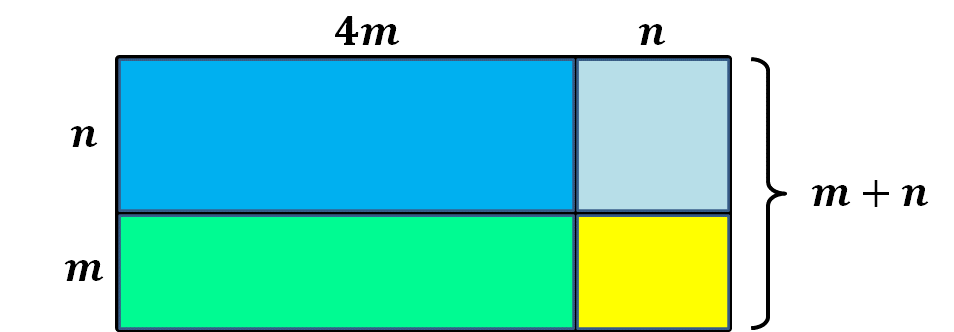
Situación-problema, modelo geométrico.

 

Se requiere obtener el perímetro de un modelo geométrico que es un rectángulo, el cual está compuesto por cuatro rectángulos identificados por colores.

 

El modelo geométrico mide de largo: 4m + n y de ancho: m + n

 

 

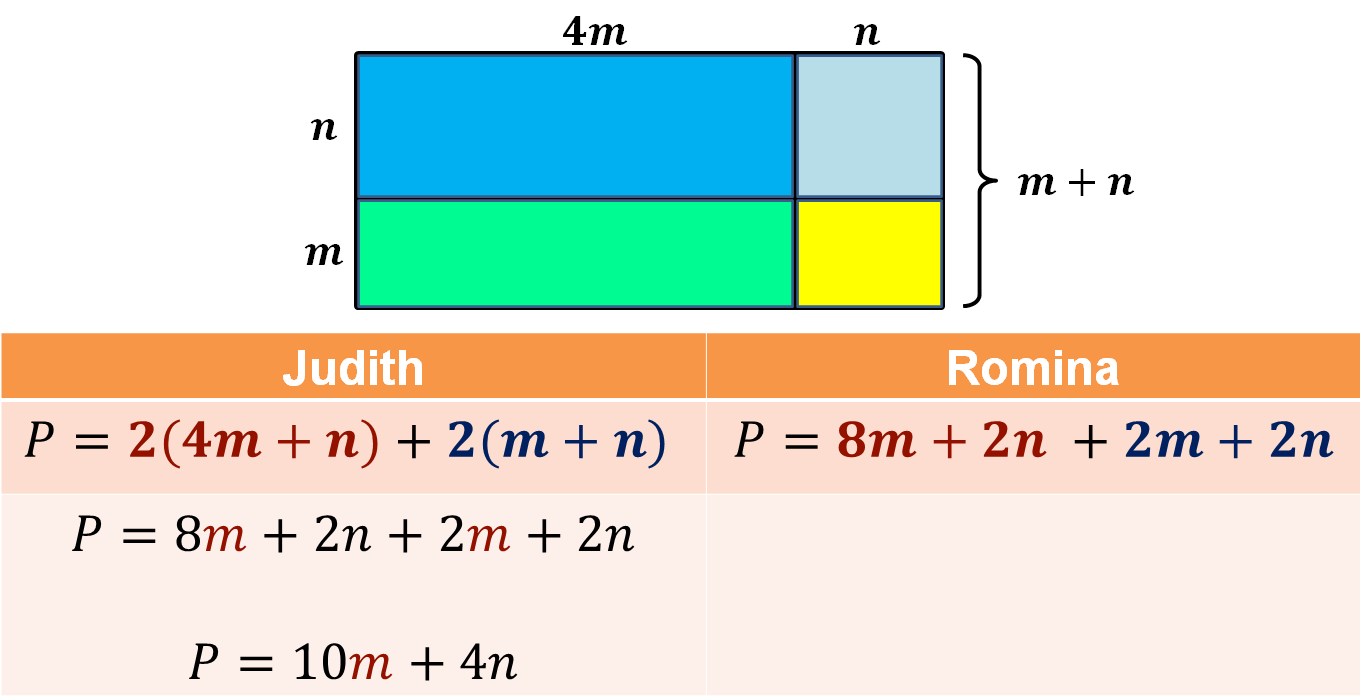
Judith modeló la expresión algebraica para el cálculo del perímetro de la siguiente manera:

 

P = 2(4m + n) + 2(m + n)

 

Mientras que Romina modeló la expresión para el cálculo del perímetro:

 

P = 8m + 2n + 2m + 2n

 

Si ambas se reducen términos semejantes, ¿sus resultados serán iguales? De ser así, ¿qué puedes concluir sobre cada una de las expresiones algebraicas que modelaron Judith y Romina?

 

Analiza los resultados:

 

Con ambas expresiones algebraicas se obtiene la misma medida, que en este caso es:

 

P = 10m + 4n

 

Se puede concluir que las expresiones algebraicas que modelaron Judith y Romina son equivalentes. Observa por qué:

 

Si se efectúa la suma de los términos semejantes, se obtiene 8m + 2m = 10m y 2n + 2n = 4n, entonces P = 10m + 4n, que es la expresión que utilizó Romina para determinar el perímetro del modelo geométrico.

 

 

En el caso de Judith, ella primero expresó el perímetro como la suma del producto de 2 por la medida de la base, que es 4m + n más el producto de 2 por la altura, que es m + n, quedando el perímetro como: P = 2(4m + n) + 2(m + n).

 

Después Judith sumó los términos semejantes: 8m + 2m = 10m y 2n + 2n = 4n

 

De esta manera, Judith obtuvo que P = 10m + 4n, que es la expresión que utilizó para determinar el perímetro del modelo geométrico.

 

 

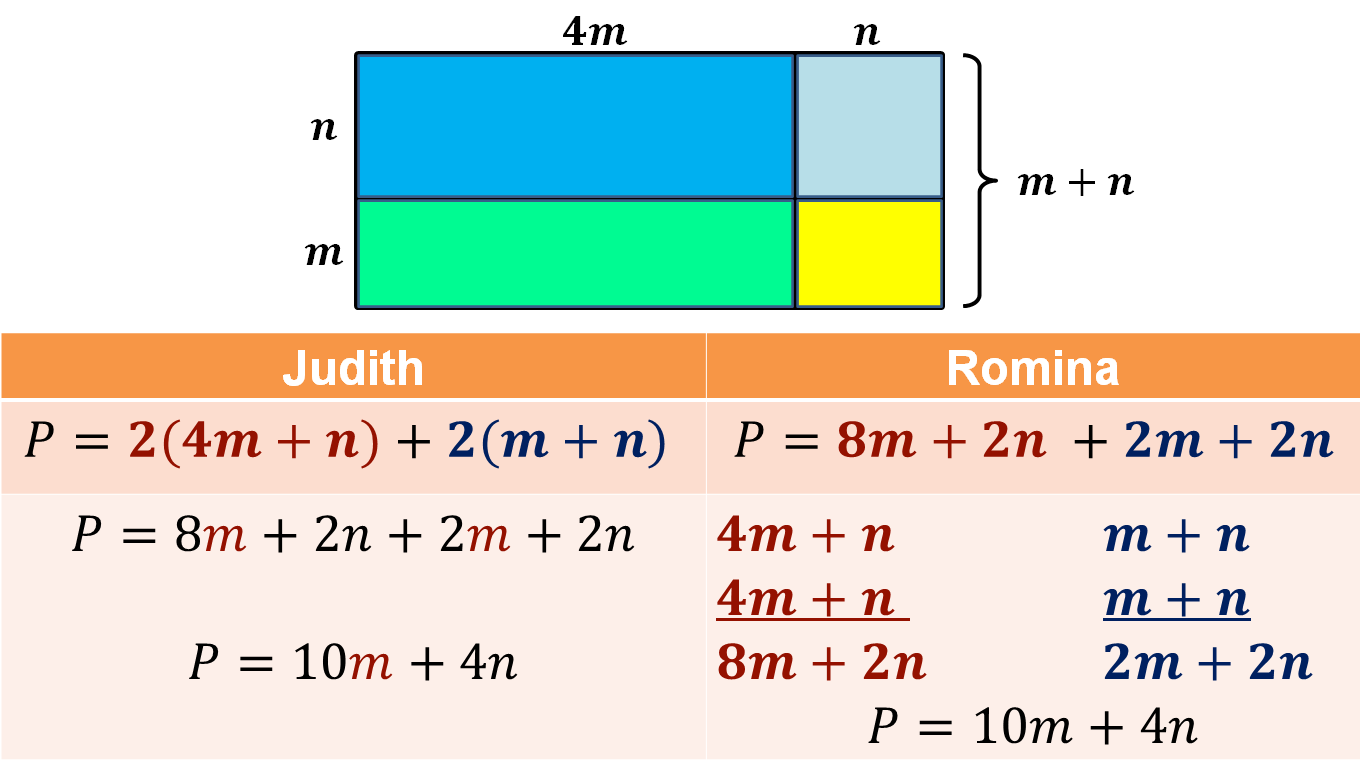
Para determinar el perímetro del modelo geométrico, Romina expresó el perímetro de manera aditiva:

 

P = 8m + 2n + 2m + 2n

 

Para establecer los sumandos de color rojo en la expresión algebraica de Romina, ella sumó dos veces la medida del largo:

 

4m + n

4m + n

 

y obtuvo 8m + 2n. Después sumó dos veces la medida del ancho:

 

m + n

m + n

 

y obtuvo 2m + 2n.

 

Ambas llegaron a un mismo resultado, y quedaron convencidas de la viabilidad de los procedimientos empleados.

 

Has analizado las expresiones algebraicas equivalentes y cómo verificar que sí lo sean.

 

Aplica lo aprendido al resolver la siguiente situación-problema. Analiza la información e intenta resolver el problema.

 

Situación-problema, cruz de cuadrados.

 

La figura está formada por cuadrados que miden “m” de lado.

 

 

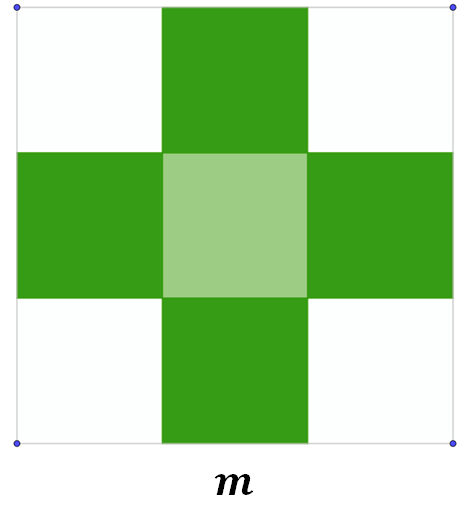
Escribe dos expresiones algebraicas equivalentes para calcular el perímetro de la cruz que se forma con los cuadrados verdes.

 

Verifica la equivalencia de las expresiones algebraicas propuestas asignando un valor numérico a la literal “m” y sustituyéndolo en cada expresión.

 

Con respecto a la indicación de escribir dos expresiones algebraicas equivalentes para calcular el perímetro de la cruz que se forma con los cuadrados verdes, Mariana, una alumna de segundo de secundaria, propone lo siguiente:

 

Se sabe que cada lado mide “m” y para determinar el perímetro de la cruz se escribe la medida de cada uno de sus lados, iniciando con el lado señalado con la flecha roja en el sentido de las manecillas del reloj hasta cerrar la cruz:

 

 

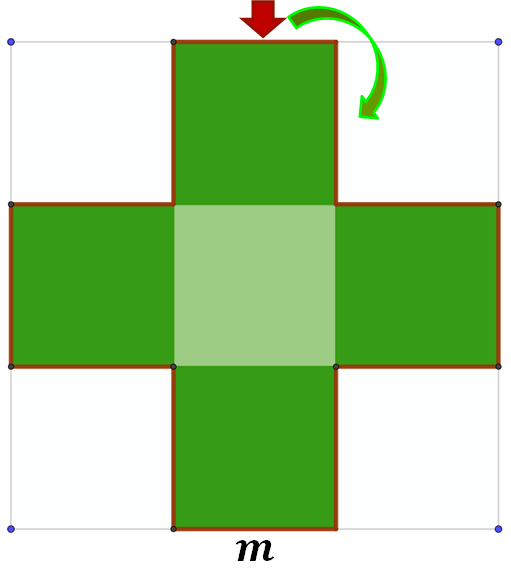
La expresión para determinar el perímetro de la cruz es:

 

P = m + m + m + m + m + m + m + m + m + m + m + m

 

P = 12m

 

Ahora, observa cómo Gerardo, otro alumno de secundaria, propone lo siguiente:

 

Como sólo tres lados de cuatro cuadrados forman el perímetro de la cruz, entonces el perímetro es 4 veces 3m, es decir:

 

P = 3m + 3m + 3m + 3m

 

Al resolver la suma se obtiene:

 

P = 12m

 

Revisa el razonamiento de Mariana y Gerardo. Ellos han propuesto escribir dos expresiones algebraicas equivalentes para calcular el perímetro de la cruz que se forma con los cuadrados verdes:

 

 

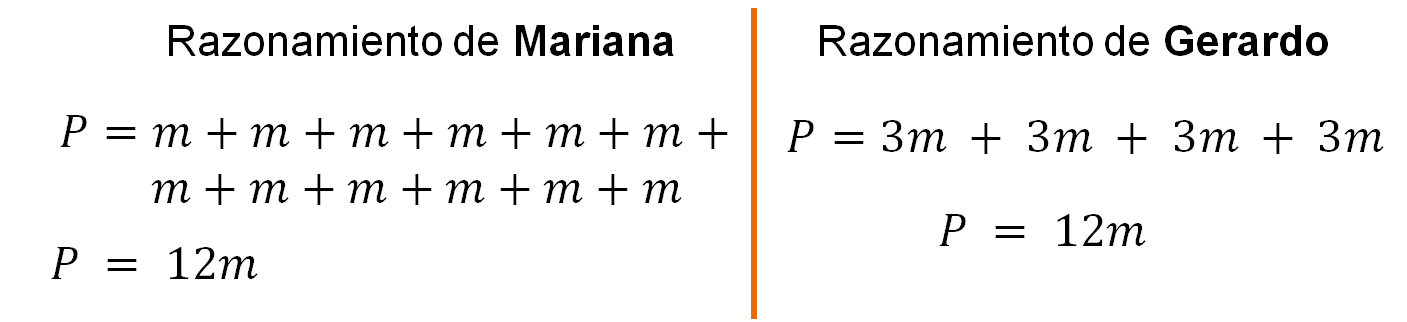
En la primera expresión, propuesta por Mariana: El perímetro es la suma de todos los lados “m”; por lo tanto, el perímetro es igual a “m” doce veces, y la suma total es 12m

 

En la segunda expresión, propuesta por Gerardo: el perímetro es 4 veces 3m, es decir, 3m + 3m + 3m + 3m = 12 m. Al resolver la suma se obtiene: P = 12m

 

Para verificar la equivalencia de las expresiones algebraicas propuestas, ellos han acordado asignar un valor numérico a la literal “m” y sustituirlo en cada expresión.

 

Mariana y Gerardo acordaron asignar a “m” el valor de 2 unidades, quedando de la siguiente manera:

 

 

En la primera expresión: El perímetro es la suma de todos los lados, por lo tanto, el perímetro es igual a 2 + 2 + 2 +… hasta tener el dos sumado doce veces. Entonces el perímetro es igual con 24 unidades.

 

En la segunda expresión: El perímetro es igual a 4 veces 3(2), es decir, 6 + 6 + 6 + 6. Al resolver la suma se obtiene: P = 24.

 

Se puede concluir que las expresiones algebraicas propuestas por Mariana y Gerardo para determinar el perímetro de la cruz son equivalentes, ya que ambas equivalen a 12m como perímetro igual. 

 

 

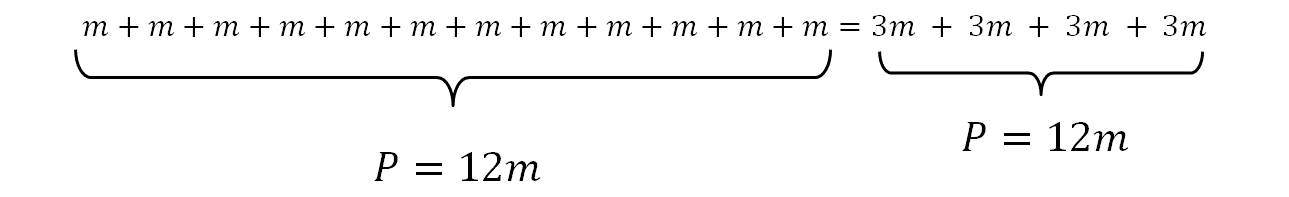
Con el estudio de las situaciones-problema anteriores puedes conjeturar y validar representaciones algebraicas del perímetro de diversas figuras geométricas. Lograste comparar y verificar que, para representar el perímetro con expresiones algebraicas, existe la posibilidad de obtener varias opciones.

 

El perímetro es la suma de la medida de los lados de cualquier figura geométrica. Has determinado el perímetro de figuras cuyas medidas se asignan por una expresión algebraica, lo que produce expresiones algebraicas al representar sus perímetros.

 

Revisa otro ejemplo para que sintetices y fortalezcas lo que has revisado.

 

Un hexágono regular, cuya medida de sus lados es “a”

 

Se sabe que el perímetro, es la suma de los lados, por lo tanto, se calcula de la siguiente manera:

 

P = l + l + l + l + l + l

 

Se sustituye la medida del lado de la siguiente manera:

 

P = a + a + a + a + a + a

 

Se reducen términos semejantes:

 

P = 6a

 

Analiza la siguiente pregunta y elige el inciso correcto:

 

¿Cuál de las siguientes expresiones es equivalente a P = 6a?

 

1. P = a + 6
2. P = 3a + 3a
3. P = 6 + 6 + 6 + 6 + 6 + 6

 

En esta sesión, con ayuda de lo que aprendiste en tus grados escolares anteriores sobre el perímetro y el procedimiento para calcularlo, pudiste deducir el perímetro de figuras cuyas medidas están dadas por valores con literales, por lo tanto, al determinar perímetros obtuviste expresiones algebraicas. De igual manera, pudiste constatar que dos expresiones algebraicas pueden representar los mismos valores.

 

Recuerden que los materiales y recursos de esta sesión, son de apoyo, y que es importante que consultes otras fuentes para enriquecer lo que aquí aprendes.

 

 

El Reto de Hoy:

 

Resuelve la siguiente situación-problema:

 

La siguiente figura es un rectángulo que mide 4p de largo y 2p de ancho.

 

Se han registrado dos expresiones algebraicas con las que se calcula su perímetro. 

 

 

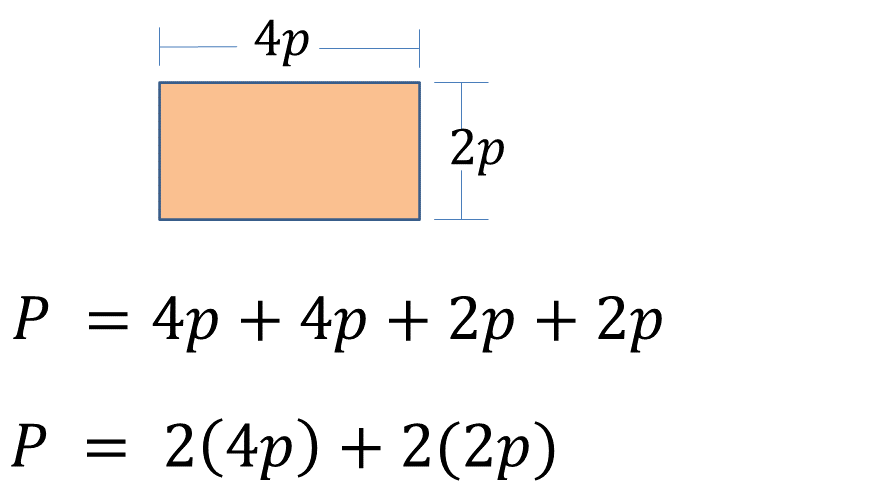
1. Plantea un problema empleando la figura, y
2. Explica con tus propias palabras por qué son, o no, equivalentes las expresiones algebraicas.