Reporte de lectura de segundo
sábado, 25 de diciembre de 2021
lunes, 20 de diciembre de 2021
martes, 9 de noviembre de 2021
SISTEMA DE MEDIDAS (SEGUNDOS GRADOS 09/11/2021)
ESCUELA SECUNDARIA GENERALES
TEMA: SISTEMAS DE MEDIDA.
- sistema internacional de medidasSistema de unidades internacional creado en 1960 por la Conferencia General de Pesas y Medidas para homogeneizar las unidades utilizadas en los distintos países.
¿Qué es y para qué sirve el sistema internacional de medidas?
¿Cuáles son las 7 unidades del sistema internacional?
ACTIVIDAD COMPLEMENTARIA: REALIZA EL CROQUIS DE TU VIVIENDA CON MEDIDAS, UTILIZA LAS MEDIDAD (PIE, METROS), OBTEN EL PERIMETRO DE TU VIVIENDA
MANDAR LA ACTIVIDAD AL CORREO ELECTRONICO: DANIEL30072013@OUTLOOK.COM, EN FORMATO PD, DEBE DE CONTAR CON HOJA DE PRESENTACION
viernes, 10 de septiembre de 2021
MATERIAL DE APOYO PARA EL TEMA NUEMROS CON SIGNO DE MATEMATICAS 2
MATERIAL DE APOYO PARA EL TEMA NUEMROS CON SIGNO DE MATEMATICAS 2
lunes, 9 de agosto de 2021
Temario de primer grado de secundaria
Temario de primer grado
de secundaria
Temas Aprendizajes
esperados
Número, álgebra y
variación
Número • Convierte
fracciones decimales a notación decimal y viceversa. Aproxima algunas fracciones
no decimales usando la notación decimal. Ordena fracciones y números decimales.
Adición y
sustracción
• Resuelve problemas de suma
y resta con números enteros, fracciones y decimales positivos y negativos.
Multiplicación
y división
• Resuelve problemas de multiplicación
con fracciones y decimales y de división con decimales.
• Determina y usa la jerarquía
de operaciones y los paréntesis en operaciones con números naturales, enteros y
decimales (para multiplicación y división, solo números positivos).
Proporcionalidad
• Calcula valores faltantes en problemas de proporcionalidad
directa, con constante
natural, fracción o decimal
(incluyendo tablas de variación).
• Resuelve problemas de cálculo
de porcentajes, de tanto por ciento y de la cantidad base.
Ecuaciones • Resuelve
problemas mediante la formulación y solución algebraica de ecuaciones lineales.
Funciones • Analiza y
compara situaciones de variación lineal a partir de sus representaciones
tabular, gráfica y
algebraica. Interpreta y resuelve problemas que se modelan con estos tipos de variación.
Patrones,
figuras geométricas y expresiones equivalentes • Formula
expresiones algebraicas de primer grado a partir de sucesiones y las utiliza
para analizar propiedades de la sucesión que representan.
Forma, espacio y medida
Figuras y
cuerpos geométricos • Analiza la existencia y unicidad en la construcción de triángulos
y cuadriláteros, y determina y usa criterios de congruencia de triángulos.
Magnitudes y
medidas • Calcula el perímetro de polígonos y del circulo, y áreas de triángulos
y cuadriláteros desarrollando y aplicando formulas.
• Calcula el volumen de prismas
rectos cuya base sea un triángulo o un cuadrilátero, desarrollando y aplicando
formulas.
Estadística
• Recolecta, registra y lee datos en graficas circulares.
• Usa e interpreta las
medidas de tendencia central (moda, media aritmética y mediana) y el rango de
un conjunto de datos y decide cuál de ellas conviene más en el análisis de los datos
en cuestión.
Probabilidad
• Realiza experimentos aleatorios y registra los resultados para
un acercamiento a la probabilidad frecuencial.
MATEMÁTICAS EN LA EDUCACIÓN BÁSICA CICLO ESCOLAR 2021- 2022
CICLO ESCOLAR 2021- 2022
MATEMÁTICAS EN LA EDUCACIÓN BÁSICA
Las matemáticas son un conjunto de conceptos, métodos y técnicas mediante los cuales es posible analizar fenómenos y situaciones en contextos diversos; interpretar y procesar información, tanto cuantitativa como cualitativa; identificar patrones y regularidades, así como plantear y resolver problemas. Proporcionan un lenguaje preciso y conciso para modelar, analizar y comunicar observaciones que se realizan en distintos campos.
Así, comprender sus conceptos fundamentales, usar y dominar sus técnicas y métodos, y desarrollar habilidades matemáticas en la educación básica tiene el propósito de que los estudiantes identifiquen, planteen, y resuelvan problemas, estudien fenómenos y analicen situaciones y modelos en una variedad de contextos.
Además de la adquisición de un cuerpo de conocimientos lógicamente estructurados, la actividad matemática tiene la finalidad de propiciar procesos para desarrollar otras capacidades cognitivas, como clasificar, analizar, inferir, generalizar y abstraer, así como fortalecer el pensamiento lógico, el razonamiento inductivo, el deductivo y el analógico.
PROPÓSITOS GENERALES:
1. Concebir las matemáticas como una construcción social en donde se formulan y argumentan hechos y procedimientos matemáticos.
2. Adquirir actitudes positivas y críticas hacia las matemáticas: desarrollar confianza en sus propias capacidades y perseverancia al enfrentarse a problemas; disposición para el trabajo colaborativo y autónomo; curiosidad e interés por emprender procesos de búsqueda en la resolución de problemas.
3. Desarrollar habilidades que les permitan plantear y resolver problemas usando herramientas matemáticas, tomar decisiones y enfrentar situaciones no rutinarias.
PROPÓSITOS POR NIVEL EDUCATIVO
Propósitos para la educación preescolar:
1. Usar el razonamiento matemático en situaciones diversas que demanden utilizar el conteo y los primeros números.
2. Comprender las relaciones entre los datos de un problema y usar procedimientos propios para resolverlos.
3. Razonar para reconocer atributos, comparar y medir la longitud de objetos y la capacidad de recipientes, así como para reconocer el orden temporal de diferentes sucesos y ubicar objetos en el espacio.
Propósitos para la educación primaria:
1. Utilizar de manera flexible la estimación, el cálculo mental y el cálculo escrito en las operaciones con números naturales, fraccionarios y decimales.
2. Identificar y simbolizar conjuntos de cantidades que varían proporcionalmente, y saber calcular valores faltantes y porcentajes en diversos contextos.
3. Usar e interpretar representaciones para la orientación en el espacio, para ubicar lugares y para comunicar trayectos.
4. Conocer y usar las propiedades básicas de triángulos, cuadriláteros, polígonos regulares, círculos y prismas.
5. Calcular y estimar el perímetro y el área de triángulos y cuadriláteros, y estimar e interpretar medidas expresadas con distintos tipos de unidad.
6. Buscar, organizar, analizar e interpretar datos con un propósito específico, y luego comunicar la información que resulte de este proceso.
7. Reconocer experimentos aleatorios y desarrollar una idea intuitiva de espacio muestral.
Propósitos para la educación secundaria:
1. Utilizar de manera flexible la estimación, el cálculo mental y el cálculo escrito en las operaciones con números enteros, fraccionarios y decimales positivosy negativos.
2. Perfeccionar las técnicas para calcular valores faltantes en problemas de proporcionalidad y cálculo de porcentajes.
3. Resolver problemas que impliquen el uso de ecuaciones hasta de segundo grado.
4. Modelar situaciones de variación lineal, cuadrática y de proporcionalidad inversa; y definir patrones mediante expresiones algebraicas.
5. Razonar deductivamente al identificar y usar las propiedades de triángulos, cuadriláteros y polígonos regulares, y del círculo. Asimismo, a partir del análisisde casos particulares, generalizar los procedimientos para calcular perímetros, áreas y volúmenes de diferentes figuras y cuerpos, y justificar las fórmulas para calcularlos.
6. Expresar e interpretar medidas con distintos tipos de unidad, y utilizar herramientas como el teorema de Pitágoras, la semejanza y las razones trigonométricas, para estimar y calcular longitudes.
7. Elegir la forma de organización y representación —tabular, algebraica o gráfica— más adecuada para comunicar información matemática.
8. Conocer las medidas de tendencia central y decidir cuándo y cómo aplicarlas en el análisis de datos y la resolución de problemas.
9. Calcular la probabilidad clásica y frecuencial de eventos simples y mutuamente excluyentes en experimentos aleatorios.
jueves, 1 de julio de 2021
CALIFICACIONES DEL TRIMESTRE TRES ESCUELA FERNANDO LOPEZ ARIAS
SEGUNDO GRADO GRUPO "E"
SEGUNDO GRADO GRUPO "F"
TERCERO E
martes, 29 de junio de 2021
Matemáticas y economía
TERCEROS AÑOS
Matemáticas y economía
Aprendizaje esperado: Analiza y compara diversos tipos de variación a partir de sus representaciones tabular, gráfica y algebraica, que resultan de modelar situaciones y fenómenos de la física y de otros contextos
Énfasis: Analizar situaciones asociadas a fenómenos de la economía.
¿Qué vamos a aprender?
Ten a la mano tu cuaderno, lápiz y goma.
Una de las relaciones más conocidas y cotidianas de la matemática en las actividades humanas, es la referente a situaciones como el cálculo de los costos de producción de artículos, la cotización del precio final de un producto, en el margen de ganancia y en el pago de los impuestos que se generan al vender los artículos, entre otros.
Para dar un ejemplo, considerarás que los productos que adquieres pueden o no estar gravados por un impuesto dependiendo del rubro al que pertenecen.
En estos ejemplos, se observará directamente la relación matemática con las actividades económicas.
¿Qué hacemos?
En nuestro país se tiene el conocido como IVA, que es el impuesto al valor agregado de un producto y que tiene como finalidad la recaudación de recursos para el estado.
El IVA es un impuesto al consumo que se impone sobre el valor que se agrega a un producto o servicio.
Tomando como ejemplo un saco, considera que ese producto está gravado con un 16 por ciento de su valor comercial, que tu como consumidor debes pagar por el hecho de adquirir el producto en cuestión.
Pero, ¿cómo se puede calcular?
Observa el siguiente audiovisual para conocer más al respecto.
- Con el IVA incluido
https://www.youtube.com/watch?v=ghcZ23w6668
Revisa la siguiente situación:
Resuelve utilizando el saco como ejemplo. Si consideras su precio en 1000 pesos sin el IVA, se tiene:
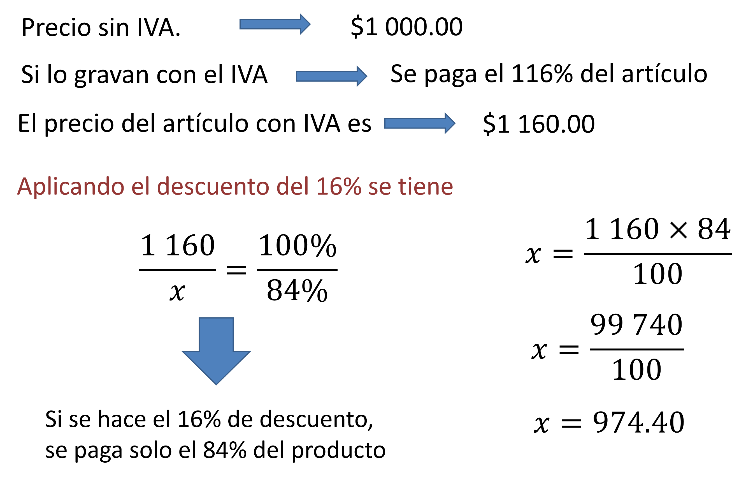
El precio sin IVA es de 1000 pesos.
Si lo gravan con el IVA entonces se está pagando el 116 por ciento del precio inicial de los 1000 pesos.
Así el precio con IVA es de 1 160 pesos
Ahora, si a 1 160 pesos le aplicas el descuento del 16 por ciento que ofrece el comerciante, se tiene:
1 160 es el 100 por ciento, “x” representa al 84 por ciento.
¿Por qué representa al 84 por ciento?
Si el artículo tiene un 16 por ciento de descuento, estarás pagando el 84 por ciento del precio total de artículo, ya que 100 menos 16 es 84.
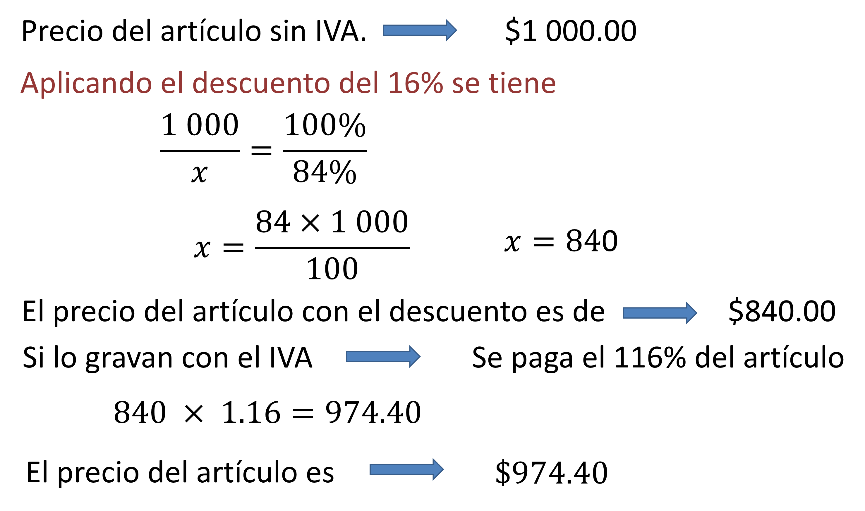
Siguiendo esa línea de razonamiento entonces si se aplica el 16 por ciento de descuento al precio del artículo sin IVA se tiene:
1 000 es el 100 por ciento, como “x” es el 84 por ciento.
Se resuelve y “x” es igual a 84 por 1 000 entre 100 que es igual a 840.
Ahora se debe gravar con el IVA del 16 por ciento.
Así que se multiplica 840 por 1.16 y se obtiene 974.40.
Así, al comparar se puede observar que en ambos casos el precio final que se paga es el mismo.
Ahora, observa otra aplicación que corresponde al ámbito económico de un país.
Se refiere al indicador llamado índice nacional de precios al consumidor.
Un índice es una medida de referencia para cuantificar la descripción de algunos fenómenos. Por ejemplo, el índice de masa corporal. Es una referencia que relaciona la estatura y el peso. Tiene una fórmula específica y sirve para dar referencia a estándares saludables.
En el caso de algunos fenómenos económicos los índices dan referencia para saber el estado de la “salud económica” de un país, por decirlo de algún modo.
Regresa al caso del índice nacional de precios al consumidor.
Observa en qué consiste en el audiovisual, del minuto 04:18 a 06:10.
- Índices
https://www.youtube.com/watch?v=zqmDt34oHcQ
Las variaciones del INPC se consideran una buena aproximación de las variaciones de los precios de los bienes y servicios comercializados en el país. De ahí que sea el indicador oficial de la inflación en México.
Entonces es un indicador económico que facilita la toma de decisiones con respecto al comportamiento de los precios.
Cabe resaltar que desde el año 2011 el proceso de obtención del INPC, está a cargo del INEGI.
El proceso de cálculo del mismo incluye siete etapas:
El INPC tiene una periodicidad quincenal.
Pero, ¿cómo puede conocer la inflación entre dos fechas?
Para determinar esto se usa la fórmula:
Índice del periodo actual entre el índice del periodo anterior, se le resta la unidad y al resultado se le multiplica por 100.
Por ejemplo, para conocer la inflación anual entre 2019 y 2020, se dividen los índices, el de junio de 2020, entre el correspondiente a junio de 2019, al resultado obtenido se le resta la unidad y se multiplica por 100.
El INPC de junio de 2020 es de 107.4 y el del mes de junio de 2019 es de 103.9.
La división entre 107.4 y 103.9, menos 1 y multiplicando por 100, da como resultado 3.3.
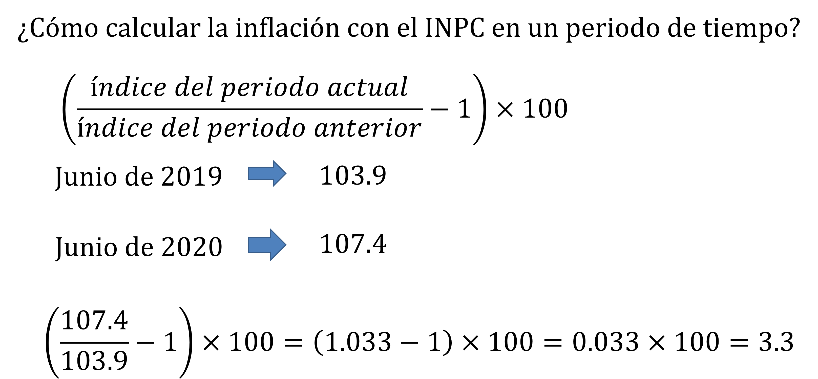
Es decir, la inflación aumentó 3.3 % de junio del 2019 a junio de 2020.
Ahora observa una gráfica que muestra datos actualizados a los primeros meses de 2021.
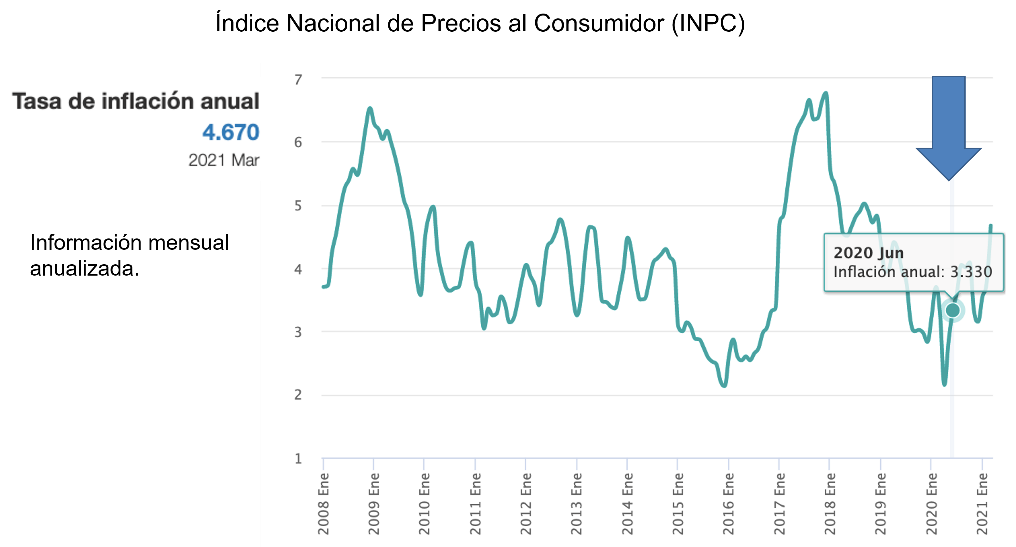
Se hace la consideración de que la inflación en el periodo anual de marzo de 2020 a marzo de 2021 es de 4.670
¿A qué se refiere con información mensual anualizada?
Se refiere a que se muestra la información por mes en referencia a la inflación del mismo mes de un año anterior.
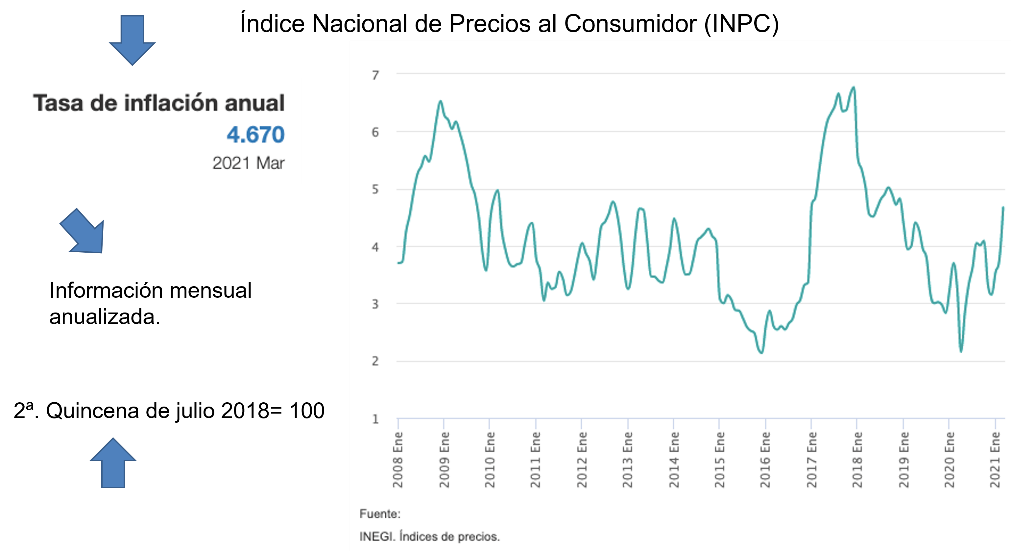
Por eso en la gráfica puedes observar que la inflación del mes de junio de 2020 es la que ya calculas antes con respecto a la de junio de 2019.
También se puede ver en la gráfica la acotación que se toma como referencia el índice de la inflación de julio de 2018.
Cuando se trabaja con índices es necesario tener un punto de referencia que esté actualizado y que considere que lo sucedido en ese periodo se haya mantenido sin graves fluctuaciones por eventos adicionales a lo que se considera.
Por ejemplo, no puede ser referencia un periodo de tiempo en donde se dio una sequía, un huracán o un movimiento social que cause demasiadas fluctuaciones en los precios.
Antes el INPC tenía como referencia el año 2010.
Para entender mejor observa otra gráfica.
En esta segunda gráfica puedes observar ver que la escala de valores de eje vertical es diferente. Se tienen datos negativos y positivos a diferencia de la primera gráfica.
Lo que es conveniente en esta gráfica es encontrar el punto de referencia, es decir, en que quincena está localizado el cero.
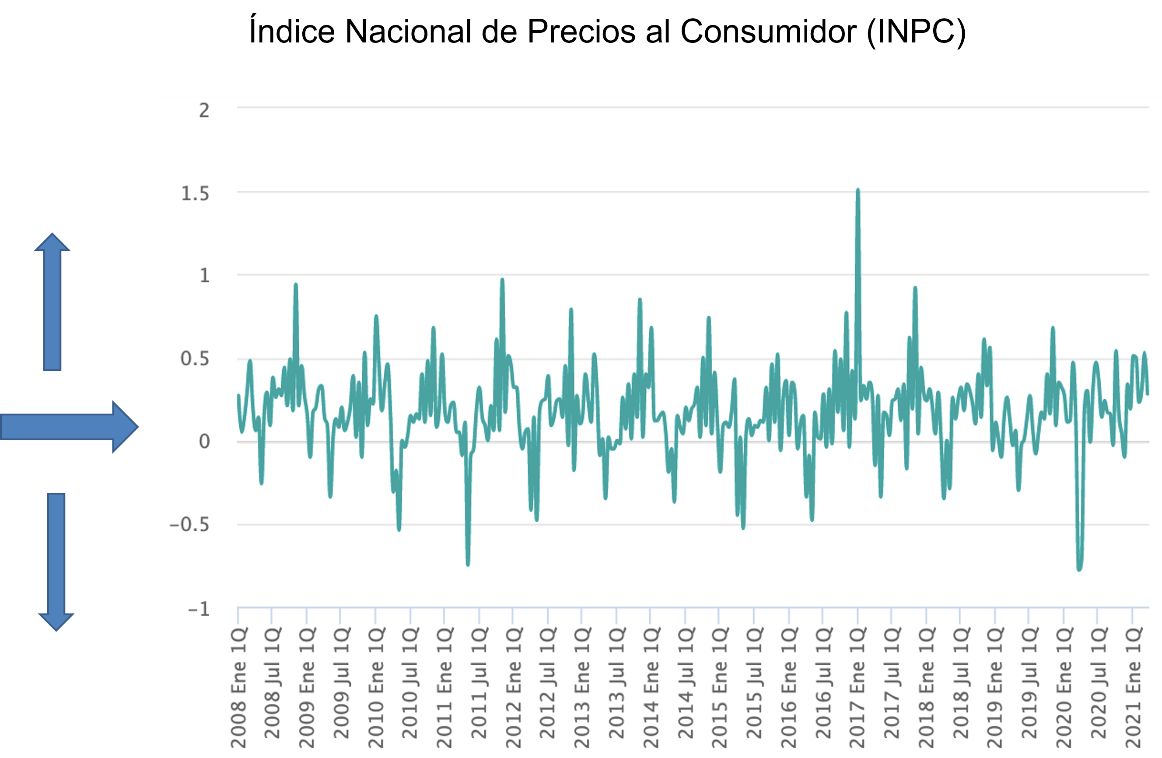
Se observa que es algo difícil debido a que los datos fluctúan mucho de mes a mes.
Utiliza entonces la tabla de datos que corresponde a la gráfica mostrada.
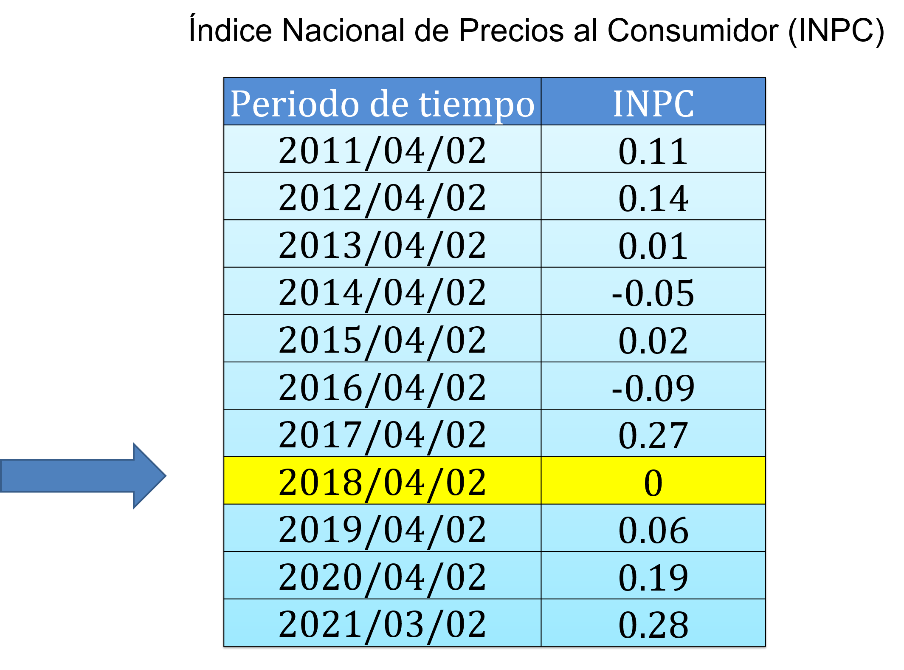
Realizando esa búsqueda y en referencia a la tabla que se muestra se observa que en el año 2018 en el mes de abril el INPC tiene un valor de cero.
Es ahí en donde se encuentra el valor referencial de esta gráfica.
Se observa que efectivamente ese dato en la gráfica es cero y corresponde a la segunda quincena de 2018
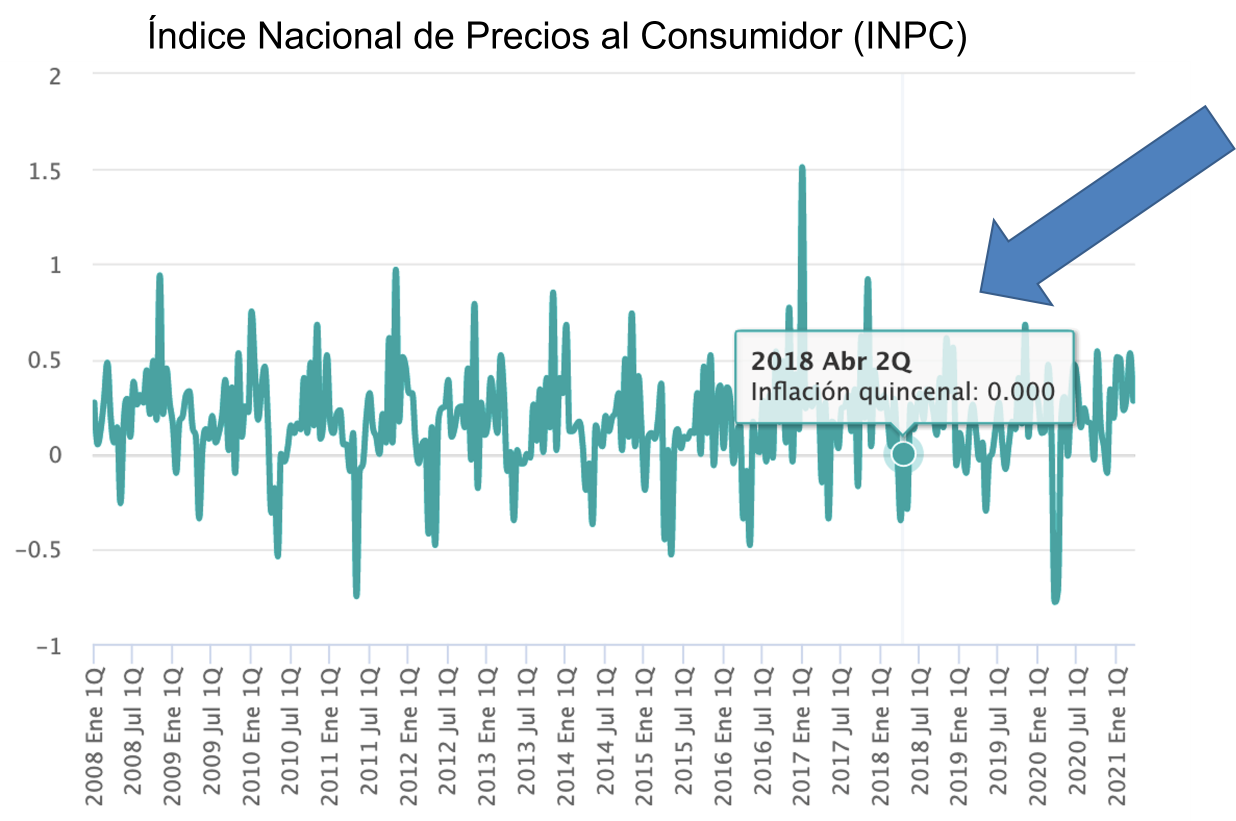
Con respecto a ese punto de referencia se puede observar que, en la gráfica para la segunda quincena del mes de marzo de 2021, el índice inflacionario corresponde a 0.280.
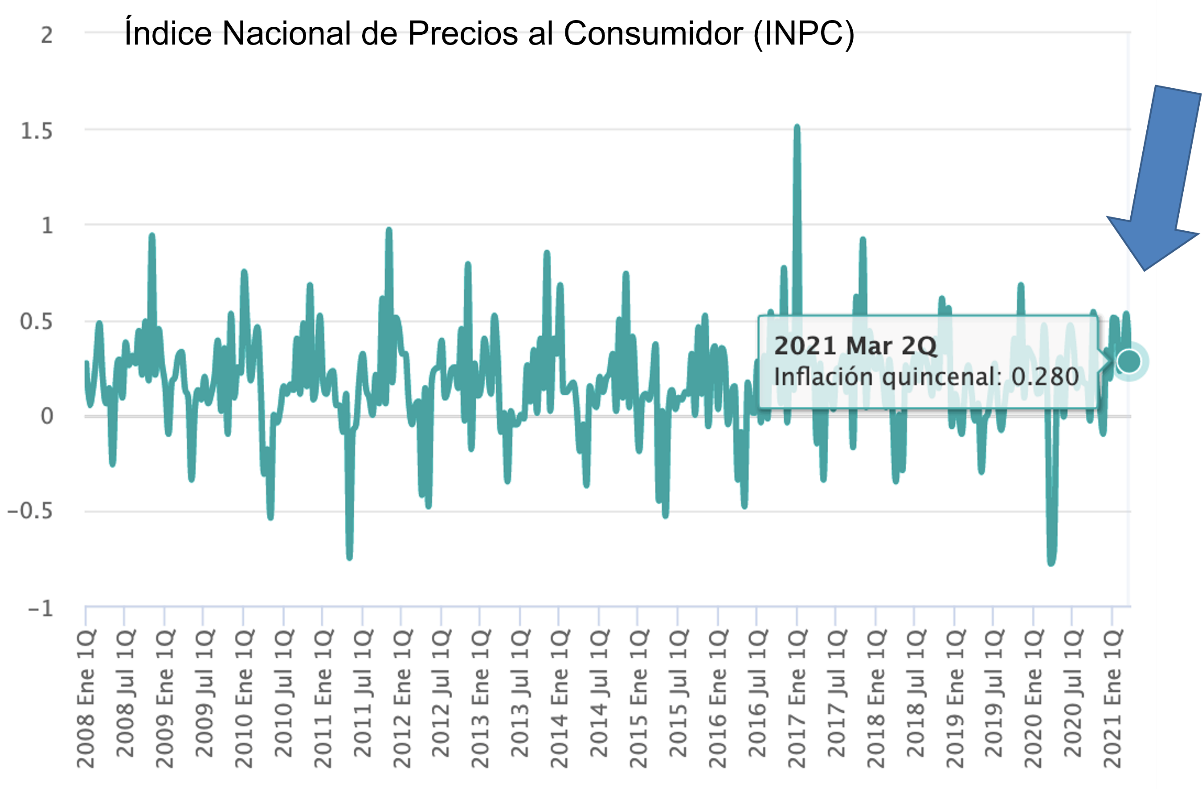
Eso indica que el INPC es mayor al punto de referencia de 2018.
Son procesos largos y complejos, que tienen muchas variables que considerar y que su duración es relativa al tiempo.
Es un proceso estadístico importante y sobre estos datos se fundan muchas de las decisiones de política económica de un país.
Para tener más claro el impacto de la matemática en la vida económica de un país o de su utilidad práctica, lee la siguiente entrevista a la profesora Anel Aranda Aguilar, ella es economista y profesora de matemáticas.
Pregunta 1. ¿Cómo se relacionan las matemáticas y la economía?
Respuesta: Existe una relación cercana. Ambas son disciplinas complementarias. La economía moderna utiliza matemáticas, y algunas partes de la investigación matemática han sido motivadas por problemas económicos.
Pregunta 2. ¿Cómo se utilizan los conocimientos matemáticos en la economía?
Respuesta: Las ciencias económicas necesitan dominar diversas e importantes herramientas matemáticas. Entre otras, el cálculo, para el estudio de funciones que permitan buscar modelos de ajuste de datos, estudiar cualitativa y cuantitativamente modelos que surjan de la teoría económica, y para la resolución de problemas de optimización que permitan repartir y asignar recursos escasos y planificar actividades.
El álgebra lineal resulta útil en la presentación y tratamiento de datos, en particular, es necesaria en el estudio cuantitativo de modelos en teoría económica y en econometría.
Pregunta 3. ¿De qué manera le son útiles las herramientas matemáticas en su trabajo?
Respuesta: Recuerdo que cuando estudiaba cálculo, álgebra o estadística, pensaba que no tendrían ninguna relación las matemáticas con mi actividad profesional, sin embargo, me doy cuenta que ahora soy capaz de actualizar conocimientos por mí misma, es decir, cuando tengo una duda busco la información que me permita resolver problemas con lógica, creatividad y confianza utilizando los conocimientos de matemáticas que aprendí y que sigo aprendiendo.
Pregunta 4. ¿Cuál es el aporte de las matemáticas en la economía?
Respuesta: Dado que los economistas trabajamos con fenómenos complejos donde las simplificaciones son necesarias y pueden aparecer algunas interferencias, la matematización de la economía ayuda a evitar errores lógicos, es decir, las matemáticas aportan estructura y rigor analítico.
Por ejemplo, los economistas formulan teorías, obtienen predicciones a partir de ellas y las someten a contrastación empírica. Si el resultado es negativo, la teoría es desechada o sustituida por otra de mayor verosimilitud.
Lo que los economistas hacemos es utilizar el método "deductivo", que consiste en formular generalizaciones acerca de la operación de factores causales relevantes, deducir de tales generalizaciones y de las condiciones iniciales predicciones concernientes a fenómenos relevantes.
Se contrastan tales predicciones, y si éstas son correctas, se considera todo el conjunto como confirmado. Si las predicciones no son correctas, se comparan explicaciones alternativas que permitan dar cuenta de lo que ha fallado.
Pregunta 5. ¿Nos puede dar un ejemplo más sobre la relación de las matemáticas y la economía?
Respuesta: Sí, claro. Consideremos que la ciencia económica se divide en dos grandes ramas: la macroeconomía y la microeconomía. La macro estudia la economía en su conjunto, los sistemas económicos de un área geográfica, empleando magnitudes colectivas o generales y tratando de obtener una visión global de su situación, con énfasis en la oferta, la demanda, los precios y los costos.
Por su parte, la microeconomía estudia el comportamiento de los consumidores y de las empresas, analiza la asignación de recursos por parte de individuos y empresas, buscando los primeros la utilidad y las segundas los beneficios, alcanzando diferentes situaciones de equilibrio.
El ejemplo del que hablaré corresponde a nivel microeconómico:
El sistema tributario mexicano ha sufrido diversas y constantes modificaciones a lo largo del tiempo, como es la variación de la tasa general del Impuesto al Valor Agregado (IVA), que se ha explicado en la sesión.
El IVA es un impuesto indirecto que se aplica al costo final de bienes y servicios. Las personas físicas, es decir individuos y morales es decir empresas, están obligadas al pago de este impuesto.
El IVA es percibido por el vendedor, al momento de una transacción comercial y lo traslada al sistema tributario. La evasión de este impuesto es difícil y su recaudación es simple. Por ejemplo, cuando vas a una tienda y compras una bebida por el que pagas $15, el 16 % corresponde al IVA, es decir $2.06 de impuesto y $12.93 es el precio del refresco, a su vez el dueño de la tienda trasladará el IVA que se paga por la bebida y lo aportará al Servicio de Administración Tributaria (SAT).
El IVA ha sufrido modificaciones a lo largo del tiempo, veamos su comportamiento desde el año de 1990 hasta el 2015.
En 1990, la tasa general del IVA era de 15 %, en ciudades fronterizas de 6 % y de 20 % para artículos de lujo. Para 1992, la tasa general se disminuye a 10 %.
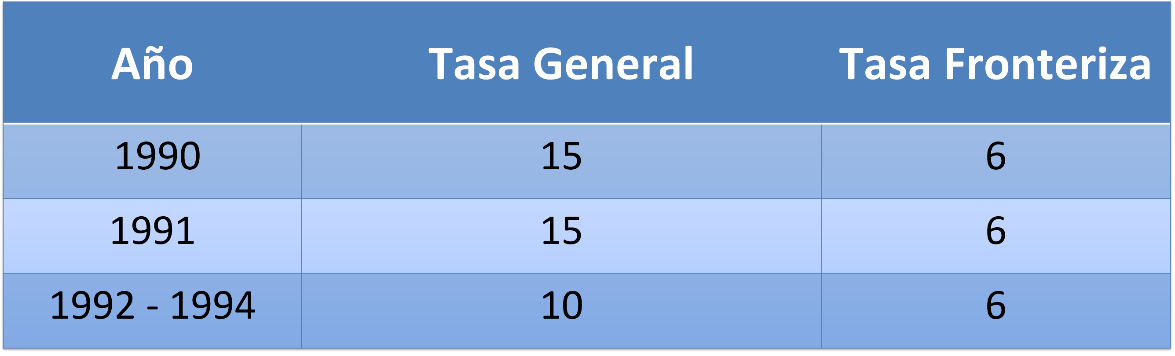
En 1995, se aumenta la tasa general del IVA a 15 % y la tasa en ciudades fronterizas a 10 %. Dichas tasas no sufrieron cambios por un período de 15 años.
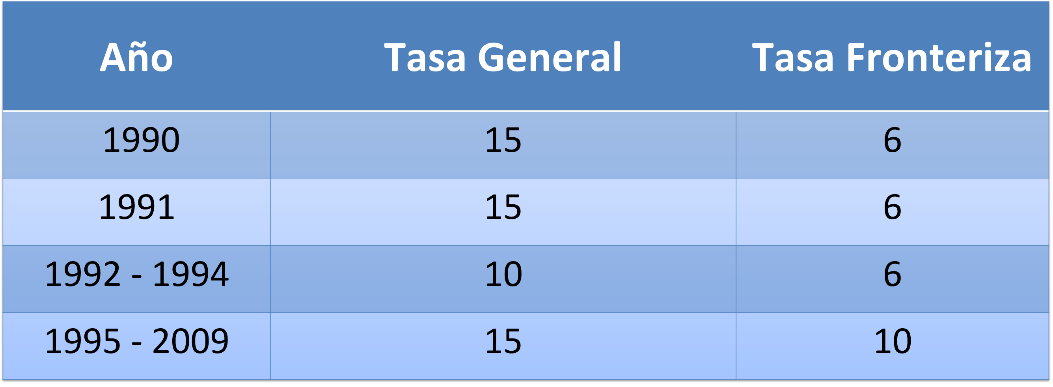
Empezando a partir de 2010, la tasa general del IVA subió a 16 % y la tasa en ciudades fronterizas a 11 %.
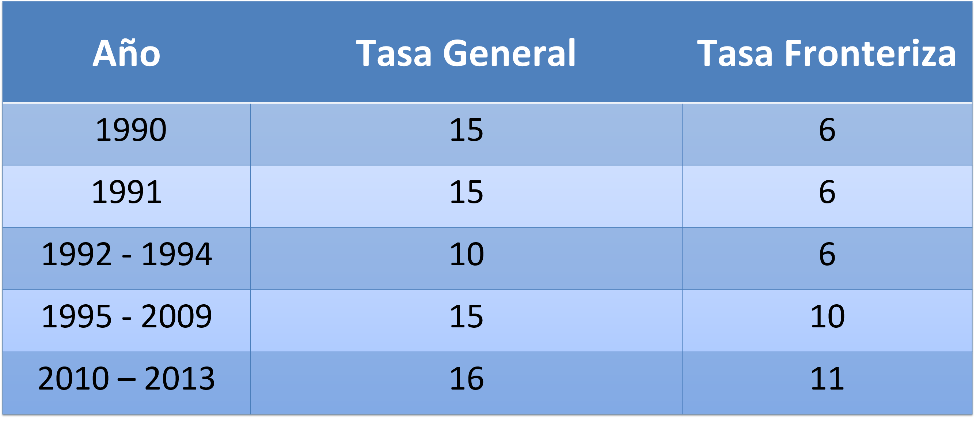
En 2014, se homologa en 16 % la tasa del IVA general y de las ciudades fronterizas.
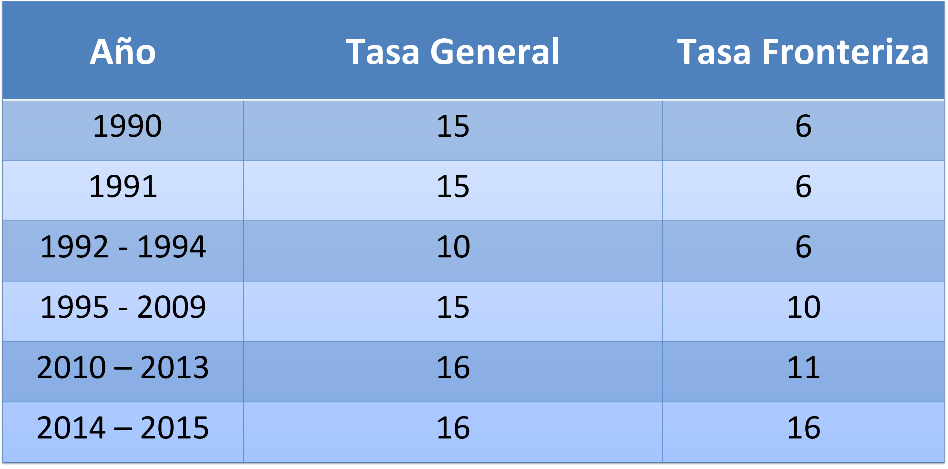
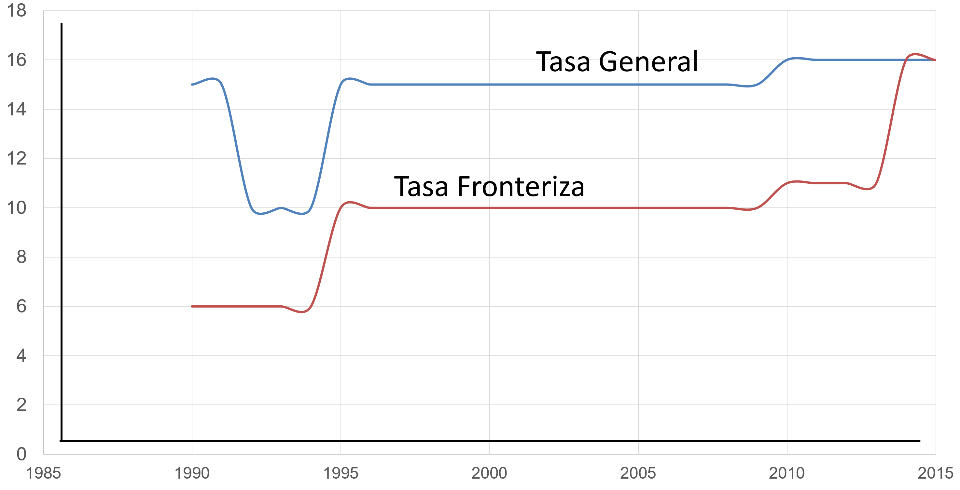
Observa la gráfica, en ella se puede leer que la tasa fronteriza fue más baja que la tasa general hasta el 2015 cuando ambas tasas se homologan. Igualmente, se lee que la tasa general era de 15 % al inicio del periodo de análisis, que está bajó y volvió a subir a 15 % por un periodo de 14 años y se incrementa nuevamente para homologarse y mantenerse en ese porcentaje.
Pregunta 6. Finalmente, ¿cuál es su consejo para las y los alumnos de secundaria con base en su experiencia con las matemáticas y la economía?
Respuesta: Piensen que tienen una caja y reúnen distintas herramientas en su interior, para que en su futuro inmediato o lejano puedan sacar cualquiera de ellas que les facilite la resolución de situaciones problema, así son las matemáticas para la economía, como una caja con distintas herramientas.
Llénenla lo más que puedan, aún con herramientas que parezcan difíciles de manejar, pero recuerden disfrutar el proceso de aprendizaje, ejercitar con dichas herramientas y verán como tendrán distintas formas de resolver situaciones fáciles o complejas.
La economía es una de las ramas del conocimiento que utiliza mucho del bagaje matemático existente y que le permite seguir desarrollándose para apoyar la aplicación de nuevos espacios en las teorías económicas.
Has trabajado en el análisis de importantes aspectos como el IVA y el INPC que son ampliamente utilizados en tu entorno.
Suscribirse a:
Entradas (Atom)
👽BIENVENIDO AL NUEVO CICLO ESCOLAR 2024 -- 2025
-
TERCEROS FECHA: 09/10/2020 Homotecia Aprendizaje esperado: Explica el tipo de transformación (reflexión, rotación o traslación) que se ap... -
JUEGO PIENSA UN NÚMERO: LA MAGIA DEL ÁLGEBRA Las actividades del tipo “Piensa un número” son actividades que apoyan con fuerza el proces... -
terceros años 23/10/2020 Binomios conjugados Aprendizaje esperado: Resuelve problemas que implican el uso de ecuaciones de segundo grado. ...