GRADO: TERCERO
FECHA: 17/09/2020
TEMA: Propiedades de las ecuaciones de segundo grado
Aprendizaje esperado: Resuelve problemas que implican el uso de ecuaciones de segundo grado.
Énfasis: Propiedades de las ecuaciones de segundo grado.
¿Qué vamos a aprender?
Anteriormente aprendiste que una ecuación, es una igualdad entre dos expresiones que contienen una o más literales llamadas incógnitas, ¿Recuerdas lo que es una incógnita? una incógnita es una cantidad desconocida.
Observa las partes que integran una ecuación
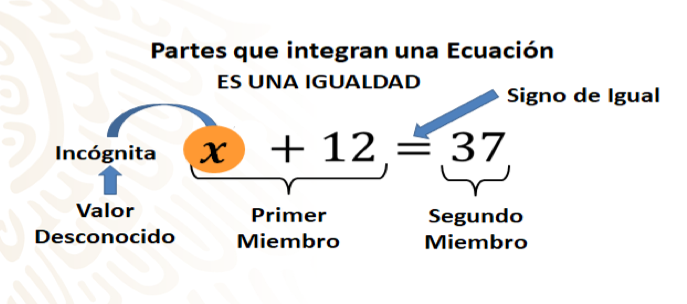
En esta ecuación x+12 =37 encontramos a la incógnita que aquí está representada por la literal x, también están presentes los miembros de la ecuación, es decir, las expresiones algebraicas separadas por el signo de igualdad. Así tenemos al primer miembro x+12 y al segundo miembro que es el número 37.
En segundo año de secundaria conociste las ecuaciones llamadas de primer grado con una incógnita, observa algunos ejemplos:
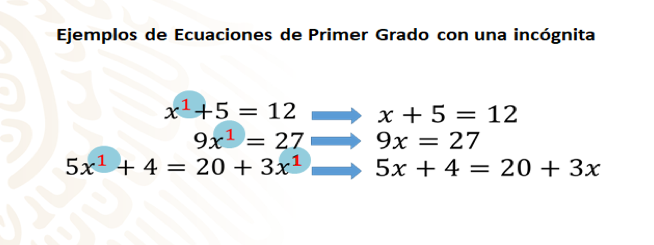
X elevado a la primera potencia + 5 = a 12, 9 por x elevado a la primera potencia =a27,5porx elevada a la primera potencia más 4 = a 20 más 3 por x elevada a la primera potencia.
Seguramente recuerdas que estas ecuaciones, las ecuaciones de primer grado, presentan como característica principal que la “incógnita” tiene como exponente máximo al número uno, el cual, por cierto, no se acostumbra escribir. Por lo tanto, ves las ecuaciones correctamente escritas: x+5=12, 9x=27 y 5x+4=20+3x
Ahora recordarás cómo se resuelven ecuaciones de primer grado de las formas (equis más o menos a igual a positivo o negativo be y a equis igual a positivo o negativo be):
| x±a=±b y ax=±b. |
¿Qué hacemos?
Observa la primera forma x±a=±b. La revisarás a través de un problema.
¿Qué número sumado a 5 da como resultado 12? Para resolverlo, primero lo escribes en lenguaje algebraico ¿Qué número sumado a 5 da como resultado 12?
Una vez planteado el problema y escrito con lenguaje algebraico procederás a deshacer las operaciones que están consideradas en la ecuación, es decir: el 5 que está sumando, pasa del otro lado de la ecuación restando. Resuelve la operación indicada en el segundo término, la resta y finalmente obtenemos el valor de la incógnita. Para comprobar que el resultado es correcto, sustituyes el valor obtenido de la incógnita x en la ecuación original y observas que 7+5=12. La igualdad se cumple.
Observa la segunda forma: ax=±b
¿Qué número multiplicado por 9 da como resultado 27? Escribes el problema en lenguaje algebraico, se despeja la incógnita x trasladando al 9 que aparece como factor, al segundo miembro como divisor. Resuelve la división y finalmente obtenemos el valor de la x. Por último, compruebas que se cumpla la igualdad sustituyendo el valor obtenido en la ecuación original.
Pero, ¿cómo distingues que una ecuación dada es de primer grado o de segundo grado? Observa las siguientes ecuaciones:
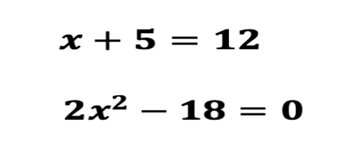

Observa los elementos y las formas básicas que tiene una ecuación de segundo grado o ecuación cuadrática:
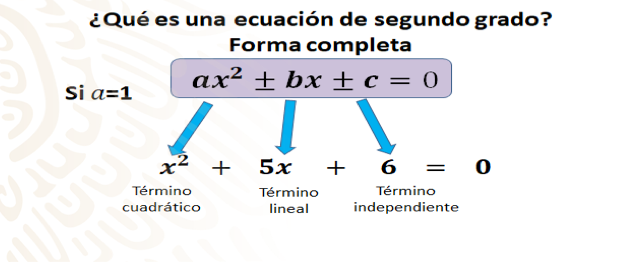
Observa primero los elementos de la forma completa de una ecuación cuadrática: tenemos al término cuadrático, que es aquel que contiene la incógnita elevada al cuadrado. Observa enseguida al término lineal que representa a la incógnita elevada a la primera potencia. Por último, tienes al término independiente, que es simplemente un número. Por cierto, cuando el coeficiente que acompaña al término cuadrático es igual a uno, no se escribe.
Ya conoces los elementos de una ecuación cuadrática. Considera lo siguiente:
En una ecuación cuadrática puede faltar el término “bx” (término lineal) o el término “c” o término independiente, pero nunca puede faltar el término ?ax?^2 por que la ecuación ya no seria de segundo grado.
A aquellas ecuaciones de segundo grado que les falte algún elemento las conocemos como ecuaciones cuadráticas incompletas. Observa:

Las ecuaciones cuadráticas incompletas se dividen en dos : las cuadráticas mixtas que son de la forma ?ax?^2±bx=0 y a las cuales les falta el término independiente o numérico y las ecuaciones cuadráticas puras que son de la forma ?ax?^2±c=0 y a las que les falta el término lineal.
Ahora identifiquen la forma que corresponda a cada ejemplo de las ecuaciones siguientes:

Corrobora tus respuestas con base en lo siguiente:

Reconociste la forma de casi todas las ecuaciones dadas, pero hay una ecuación que no corresponde hasta el momento con las formas presentadas, ¿saben cuál es?
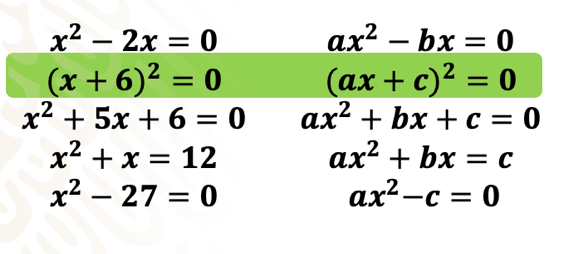
Esta forma de ecuación aprenderás a resolverla posteriormente, ya que se requiere de desarrollar el binomio al cuadrado. Ahora que ya sabes reconocer diferentes formas de ecuaciones de segundo grado es tiempo de que aprendas a resolver algunas de ellas.
Ahora realiza un primer ejercicio

Recuerda que un número es solución de una ecuación, si al sustituir dicho número por la incógnita, cumple con la igualdad.
Observa el siguiente ejemplo: 5 es solución de la ecuación x^2= 25, porque al sustituir 5 en el lugar de la incógnita x^2 , obtienes que 5^2=25
Entonces…

Una vez que hayas logrado sustituir cada número en las dos ecuaciones y comprobado que se cumple la igualdad,
¿Cuántas soluciones encontraste para cada una de las ecuaciones?
Analiza tus respuestas.
Si resolviste que: para la ecuación 3x=12 el número 4 positivo es la única solución, es correcto, pues al sustituir el número 4 por la incógnita x, tenemos: 3(4)=12, así ninguno de los otros números -4,-3 y 3 son soluciones , porque no cumplen la igualdad. Y, si resolviste que para la segunda ecuación x2-x-12=0 los números 4 positivo y cuatro negativo son soluciones, también es correcto, ambos al ser sustituidos por la incógnita cumplen con la igualdad, esto es 4^2-4-12=0 y (-4)^2-4-12=0
¿En cuál de las ecuaciones obtuviste una solución y en cuál dos?
· En la ecuación en la que obtienes dos soluciones ¿cuál es el exponente máximo de la incógnita?
Observa el siguiente ejemplo:

Observa las ecuaciones a, b y c, ¿A cuál de ellas se parece el ejemplo?

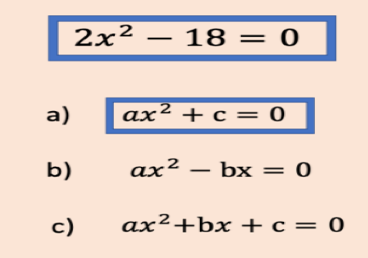
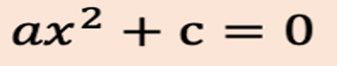
Para resolver una ecuación cuadrática del tipo ax^2+c=0
Primero:
1. Despejas la incógnita x^2

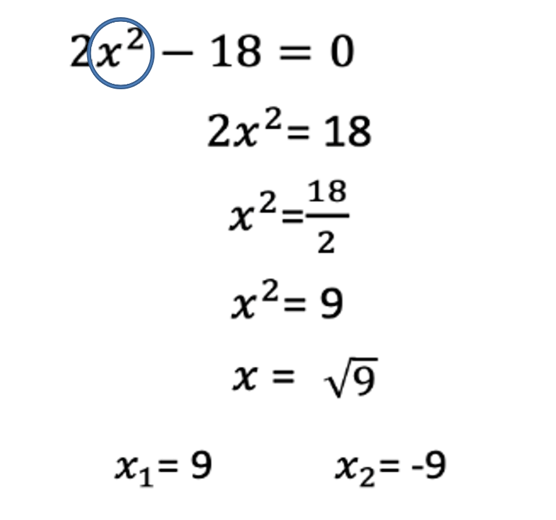
2. Una vez despejada, utilizas la operación inversa de la potenciación, es decir la raíz cuadrada en ambos términos para obtener las soluciones de la ecuación.
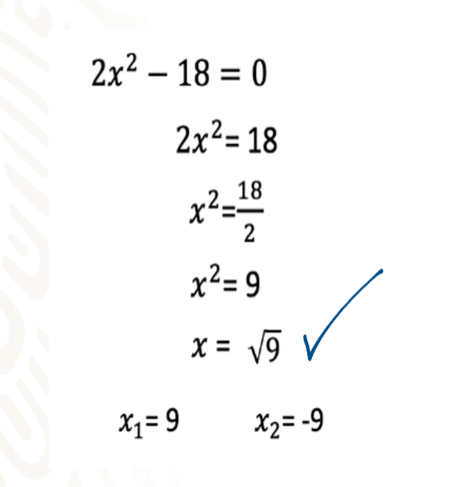
3. De esta manera obtendrás las dos soluciones de esta ecuación de segundo grado.
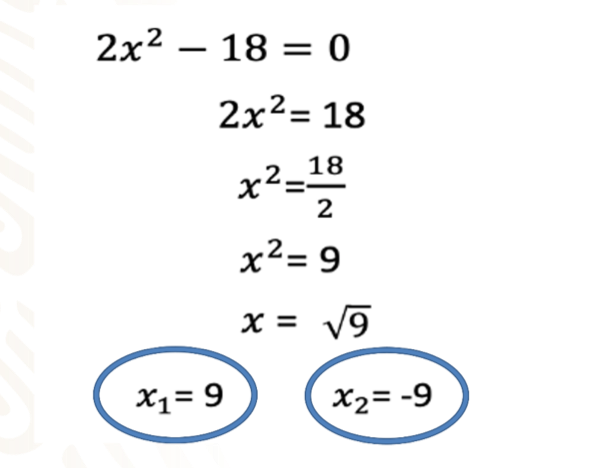
Otra característica de una ecuación de segundo grado es que tiene dos soluciones.
El Reto de Hoy:
Recuerda:

¡Buen trabajo!


No hay comentarios.:
Publicar un comentario