Volumen de prismas rectos
Aprendizaje esperado: Calcula el volumen de prismas rectos, cuya base sea un triángulo o un cuadrilátero, desarrollando y aplicando fórmulas.
Énfasis: Calcular el volumen y las medidas de prismas rectos.
¿Qué vamos a aprender?
Calcularás el volumen de prismas cuya base sea un triángulo o un cuadrilátero. Además, analizarás las fórmulas, las cuales te permiten obtener cualquier medida de los prismas.
¿Qué hacemos?
La geometría es una de las ramas de las matemáticas que ha inspirado a muchas personas a lo largo de la historia, para realizar numerosas creaciones. Por ejemplo, arquitectos y artistas se han basado en figuras geométricas para crear esculturas, construir edificios, monumentos y muchas cosas más de distintos tamaños, formas y colores.
En todo el mundo se pueden apreciar estas creaciones y en México también, por lo que es muy probable que identifiques objetos o edificaciones a tu alrededor con formas geométricas. Por otro lado, además del lado estético, está el lado funcional, ya que hay edificios que alojan a una gran cantidad de personas debido a sus dimensiones y al volumen que pueden contener.
Por ejemplo, en el corazón de la Ciudad de México, se encuentra la Torre Latinoamericana, que tiene una altura de más de 180 metros, con 44 niveles y en la que caben, aproximadamente, 10 mil personas. Esta Torre, tiene la forma de un prisma, cuyas caras laterales son cuadriláteros y su base tiene forma cuadrangular. Está inspirada en el edificio Empire State de la ciudad de Nueva York y es uno de los rascacielos latinoamericanos más altos.

https://www.instagram.com/p/BzySS4HjjiC/?igshid=vxwfgklwhvy5
Este tipo de edificaciones puede albergar a muchas personas debido al volumen que tiene, por lo que se convierten en importantes puntos de trabajo y turismo de las comunidades en las que se construyen.
En la Ciudad de México hay otro rascacielos más alto que la Torre Latinoamericana, cuya base no es cuadrangular sino rectangular, se trata del World Trade Center de la Ciudad de México. Ambos rascacielos tienen la forma de prismas, aunque la forma de sus bases es diferente.
En esta ocasión, vas a aprender cómo calcular el volumen de distintos tipos de prismas. Los prismas son formas muy comunes a tu alrededor, por lo que conocer cómo calcular el volumen de estas figuras puede ser de utilidad, para que conozcas más sobre el tema revisa el siguiente audiovisual.
- 29. El volumen de prismas rectangulares.
Revisa del minuto 00:56 al 01:06 y del 01:25 al 02:48.
Como pudiste observar, las unidades de medida del volumen son unidades cúbicas. En el video, se calculó el volumen de un prisma cuya base es rectangular y se hizo con pequeños cubos de madera que representaron las unidades cúbicas.
El cálculo se desarrolló analizando la construcción del prisma, es decir, agregando niveles al cuerpo geométrico. Se comenzó con el primer nivel, que representa la base del prisma y se fueron agregando niveles, que representan la altura del prisma.
Como viste, es posible agregar niveles a la base del prisma, lo que hace que la altura aumente y, en consecuencia, su volumen. Pero, ¿Qué pasaría con el volumen si a la figura de 12 cubos de base, del ejemplo, le agregarás dos niveles más? ¿Sería posible obtener una fórmula general para calcular el volumen de cualquier prisma? Para dar respuesta a estas preguntas, revisa el siguiente video.
- 29. El volumen de prismas rectangulares.
Revisa del minuto 03:05 al 03:41 y del 04:42 al 05:30
A partir de lo que viste, se puede decir que, el volumen de un prisma recto se calcula con la fórmula: Volumen = Área de la base por la altura.
Existen diferentes prismas rectos, dependiendo de la forma de su base. Por ejemplo, en el Estado de México, el arquitecto Luis Barragán se inspiró en prismas triangulares para construir unas torres con esa forma, conocidas como las Torres de Satélite y están ubicadas en el municipio de Naucalpan de Juárez. Son prismas rectos con base triangular, que con diferentes colores dan una apariencia cosmopolita a una de las vialidades más importantes del estado.

https://www.instagram.com/p/B8fxv82pFRq/?igshid=1dwk74w3v7iuo
Ya sabes cómo se calcula el volumen de un prisma rectangular, ahora, analiza cómo, a partir de ese conocimiento, se puede obtener la fórmula para la medida del volumen de un prisma triangular. Observa con atención el siguiente video:
- 62. Volumen de prismas triangulares.
Revisa del minuto 00:51 al 03:32
Como pudiste observar, en el caso de los prismas triangulares, también se cumple la fórmula general que se obtuvo antes, es decir: Volumen es igual a área de la base por la altura.
En este caso el área de la base corresponde al área de un triángulo. Recuerda que el área de un triángulo, se calcula multiplicando la base por la altura y luego dividiendo entre dos, es decir base por altura sobre dos.
Ahora, calcula el volumen de un prisma triangular cuya altura es de 10 cm y que tiene como base un triángulo rectángulo. Las medidas de dicho triángulo son: 5 cm en su lado que corresponde a su base y 4 cm en su lado que coincide con su altura.
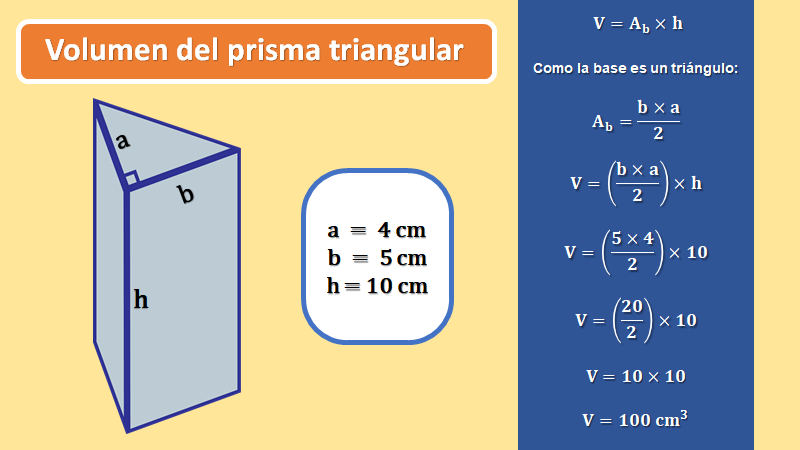
Para ello, se utiliza la fórmula, volumen igual a área de la base por altura. Si sabes que la base es un triángulo y la fórmula para calcular su área es: base por altura sobre dos, debes cambiar el área de la base por: base por altura sobre dos.
Sustituyes los datos en la fórmula, quedando: volumen es igual a 5 por 4 sobre 2 cuyo resultado se multiplica 10.
Realizas las operaciones, que son:
5 por 4, igual a 20.
20 entre dos, igual a 10.
Finalmente, 10 por 10 igual a 100.
Esto quiere decir que el volumen es igual a 100 cm cúbicos.
Parece que puedes calcular el volumen de un prisma recto, si sabes calcular el área de la base.
Escribe en tu cuaderno cuál será la fórmula para calcular el volumen de un prisma con base trapezoidal y romboidal.
Probablemente, tú ya conoces las fórmulas para calcular el volumen de esos prismas si las asocias con las fórmulas para calcular el volumen de prismas cuya base sea un cuadrilátero. ¡Presta atención! para verificar tus respuestas, después de que veas el siguiente video.
- 63. Volumen de prismas cuadrangulares.
Revisa del minuto00:37 al 05:06
Pudiste ver en el video, que para calcular el volumen de un prisma recto con base triangular, o bien, con la forma de un cuadrilátero, requiere que conozcas el área de su base. Una vez que la conoces sólo tienes que multiplicar por la altura del prisma para conocer su volumen.
Como puedes observar hay más objetos, además de edificaciones, que tienen forma de prismas rectos. Por ejemplo, ahora revisarás como calcular el volumen de un tope con forma de prisma trapezoidal que viste en el audiovisual. Para ello usarás la fórmula: volumen es igual al área de la base por la altura.
La base del prisma es un trapecio y si recuerdas, que la fórmula del área de un trapecio es igual a la suma de la Base mayor más la base menor, por su altura entre 2, puedes calcular el área de la base del tope. Solamente necesitas sustituir en la fórmula del volumen el área de la base por la fórmula del área de un trapecio, quedando: volumen es igual a Base mayor más base menor entre dos por la altura del trapecio, cuyo resultado se multiplica por la altura del prisma.
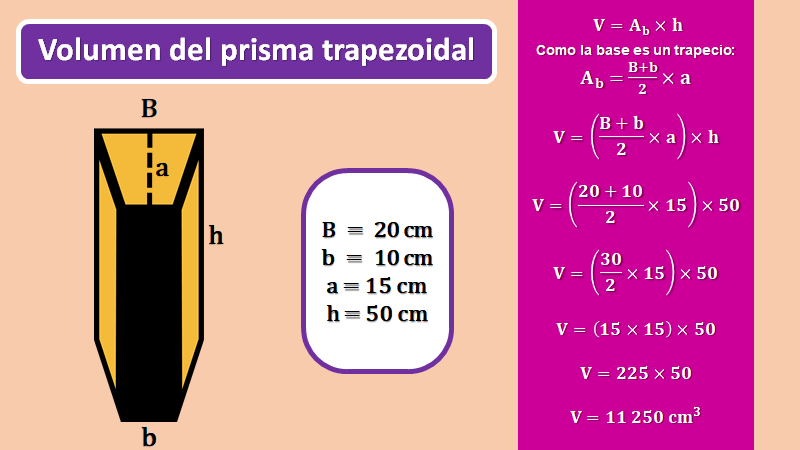
Sustituyendo los valores queda: volumen es igual a 20 más 10 sobre dos por 15, cuyo resultado se multiplica por 50.
Realiza las operaciones:
20 más 10 resulta 30.
30 sobre 2 resulta 15.
15 multiplicado por 15 resulta 225.
Finalmente, 225 por 50 resulta 11,250.
Así que el volumen es igual a 11,250 centímetros cúbicos.
Revisa otro ejemplo, en donde se calcula el volumen de la siguiente figura que es un prisma recto cuya base tiene la forma de un rombo.
La fórmula para calcular el área de un rombo es igual a diagonal mayor por diagonal menor entre 2.
Las medidas de las diagonales son: la diagonal mayor mide 20 cm de longitud y la diagonal menor mide 15 cm de longitud.
Por otro lado, es necesario conocer el volumen y para ello, se debe saber la longitud de la altura, que en este caso es de 30 cm.
Ahora, observa la fórmula para calcular el volumen del prisma. Toma nota y ve resolviendo las operaciones para calcular el volumen del prisma romboidal.
La fórmula es: A = D x d/2 es decir el área de un rombo es: Diagonal mayor por diagonal menor entre 2.
Después escribe las operaciones que son:
20 cm x 15 cm ÷ 2 = 300 cm2 ÷ 2 = 150 cm2
Sustituye los valores de la base del prisma:
El valor de la longitud de la diagonal mayor es de 20 cm que multiplicará al valor de la longitud de la diagonal menor que es 15 cm, lo que resulta 300 cm cuadrados. Después, divides el resultado entre dos, así que, el valor del área de la base del prisma es 150 cm cuadrados.
Por otro lado, como ya viste, la fórmula general para calcular el volumen de un prisma recto es: V = Abx h, es decir volumen es igual al área de la base por la altura.
Se sustituyen los valores, en donde el área de la base es de 150 cm cuadrados, que multiplica a la altura que tiene una longitud de 30 cm, lo que resulta 4,500 cm cúbicos.
150 cm2x 30 cm = 4 500 cm3
Como has visto, es posible conocer el volumen de cualquier prisma recto, si aplicas la fórmula que revisaste, es decir, si calculas el área de su base y la multiplicas por la altura.
Para ello, es necesario conocer y tener presentes las fórmulas para calcular el área del triángulo y de los cuadriláteros. A partir de la fórmula general del volumen de un prisma recto, también es posible calcular cualquier medida del prisma si se conocen, al menos, dos medidas. Es decir, si conoces la altura y el volumen, puedes calcular el área de la base.
Por ejemplo, en la fórmula general para el volumen de un prisma recto, despejas el área de la base, es decir, aplicas las propiedades de la igualdad y, como has visto, al resolver ecuaciones lineales, en ese caso la fórmula sería: Área de la base, es igual a volumen del prisma entre su altura.
Para el caso del prisma, que se revisó, conoces que el volumen es de 4,500 cm cúbicos y que su altura mide 30 cm, entonces, para conocer la medida de la base, divides 4,500 centímetros cúbicos entre 30 cm y obtienes el área de la base, que es de 150 cm cuadrados.
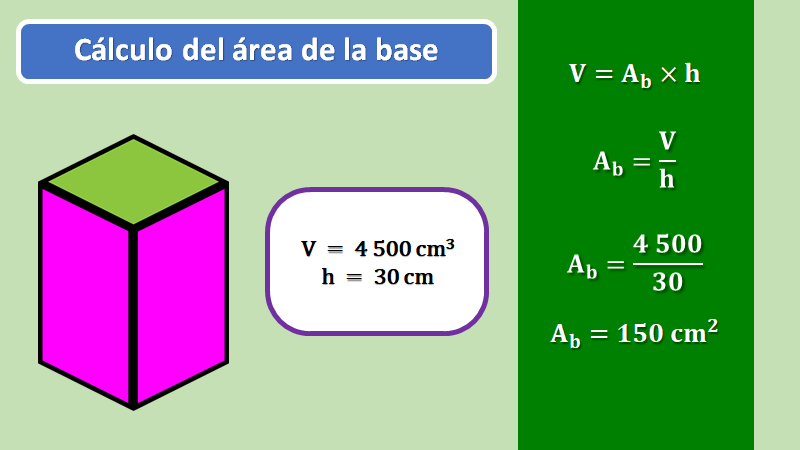
De la misma forma podrías obtener una fórmula para calcular la altura, cuando se conoce el volumen y el área de la base.
En este caso se despeja la altura. Nuevamente aplicas las propiedades de la igualdad. Así tienes que: Altura es igual a volumen entre el área de la base.
Retoma nuevamente el caso del prisma, en donde conoces que el volumen es de 4,500 cm cúbicos y que el área de la base mide 150 cm cuadrados, si divides, 4,500 cm cúbicos entre 150 cm cuadrados, obtienes la altura que es de 30 cm.
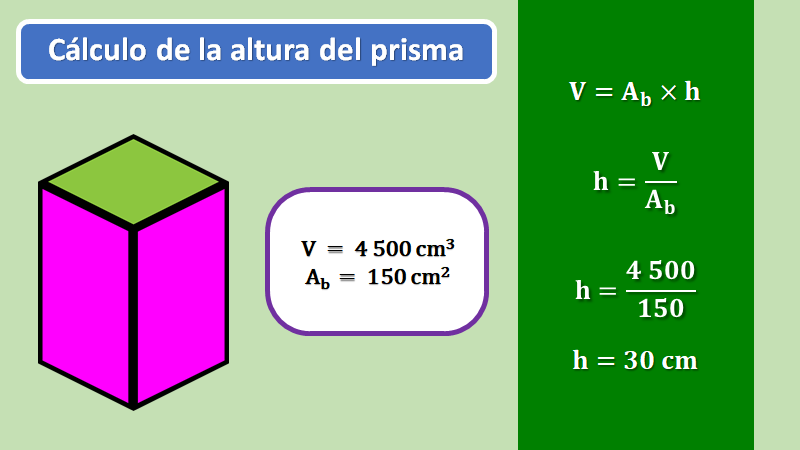
De esta forma puedes obtener cualquier medida de un prisma recto si conoces 2 de las 3 medidas involucradas en la fórmula general del volumen.
Puedes elaborar un formulario de áreas y volúmenes para organizar toda la información que has aprendido hoy. Si es posible, muéstraselo a tu maestra o maestro para recibir retroalimentación.
De igual forma si tienes alguna duda puedes solicitar la retroalimentación de tu maestra o maestro a distancia. También puedes consultar tu libro de texto en formato digital en la página oficial de la Secretaría de Educación Pública.
Has concluido el tema del día de hoy.
El reto que se propone para esta sesión es construir un prisma recto con la base que más te agrade, puede ser un cuadrilátero o un triángulo. Puedes hacerlo con cartón, plastilina o cualquier otro material moldeable; o bien, lo puedes dibujar en tu cuaderno. Decora tu prisma a tu gusto y haz uso de material reciclado que tengas a la mano.
Ya que lo hayas realizado, calcularás su volumen.


Pamela Rubí Romero Arellano (1F): https://youtu.be/64weeCZL3yc
ResponderBorrar