segundos años
24/11/2020
El perímetro y área del círculo
Aprendizaje esperado: Calcula el perímetro y el área de polígonos regulares y del círculo a partir de diferentes datos.
Énfasis: Calcular el perímetro y área del círculo a partir de diferentes datos.
¿Qué vamos a aprender?
Estudiarás la fórmula para calcular el perímetro y el área del círculo, así como su aplicación en la resolución de problemas a partir de diferentes datos.
¿Qué hacemos?
Observa el siguiente círculo y escribe dentro del paréntesis la letra que corresponda a cada uno de sus elementos.
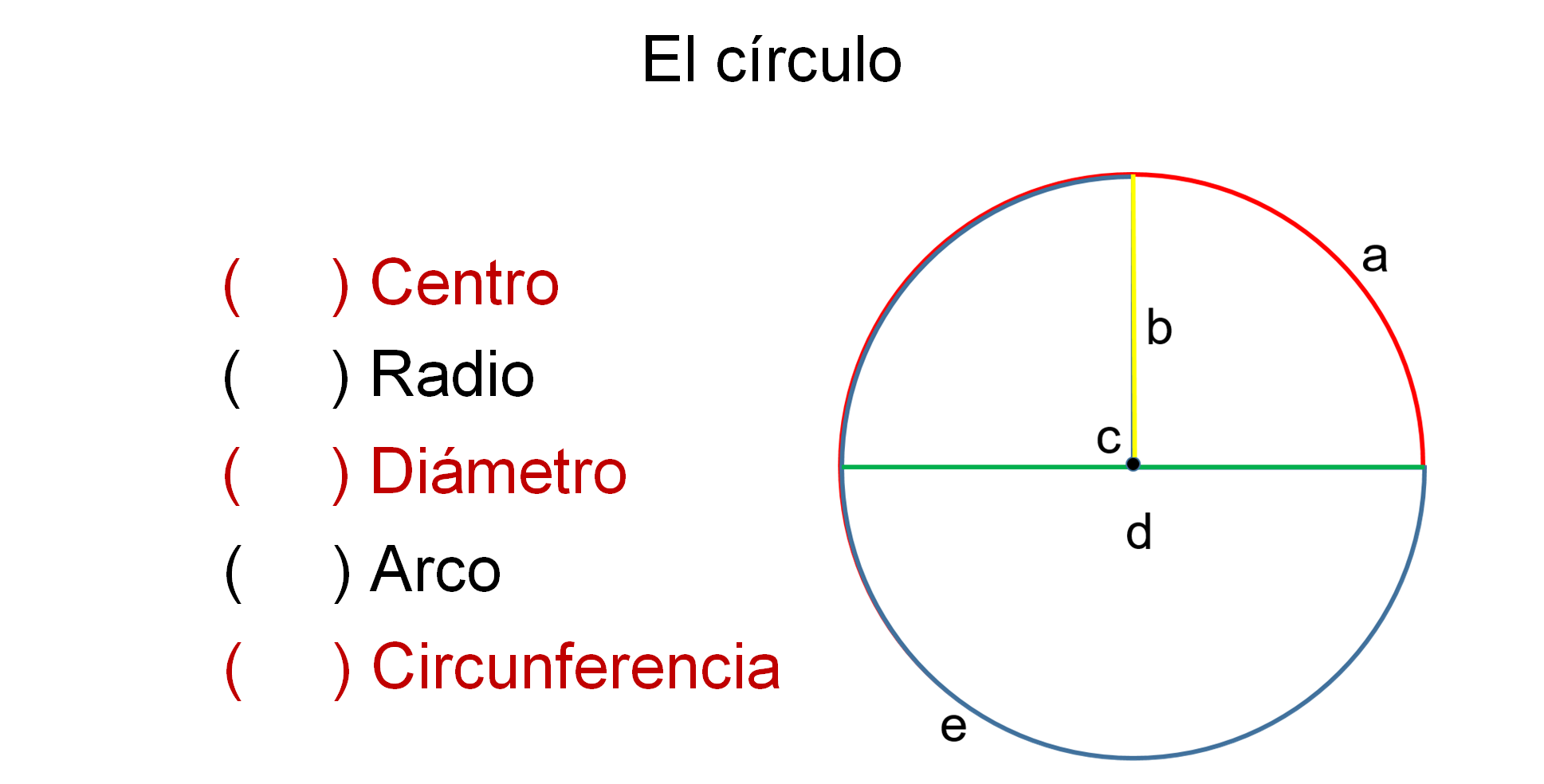
Después de elegir los elementos del circulo en la actividad anterior, verifica tus respuestas.
- La letra “a” indica el arco de la circunferencia, que es el segmento de la circunferencia que está delimitado por dos puntos diferentes pertenecientes a ésta.
- La letra “b” indica el radio del círculo, que es un segmento de recta que va del centro del círculo a cualquier punto de la circunferencia.
- La letra “c” indica el centro del círculo.
- La letra “d” indica el diámetro del círculo, que es un segmento de recta que toca dos puntos de la circunferencia y que pasa por su centro.
- La letra “e” indica la circunferencia.
Ahora, en una hoja cuadriculada, traza en la parte inferior derecha un cuadrado de cinco unidades por lado, y nombra a sus vértices A, B, C y D, como se muestra en la imagen.

Después, con centro en el vértice C, traza una circunferencia con radio igual a la longitud del lado del cuadrado, por lo que pasará por los vértices D y B. Observa la siguiente imagen como ejemplo.
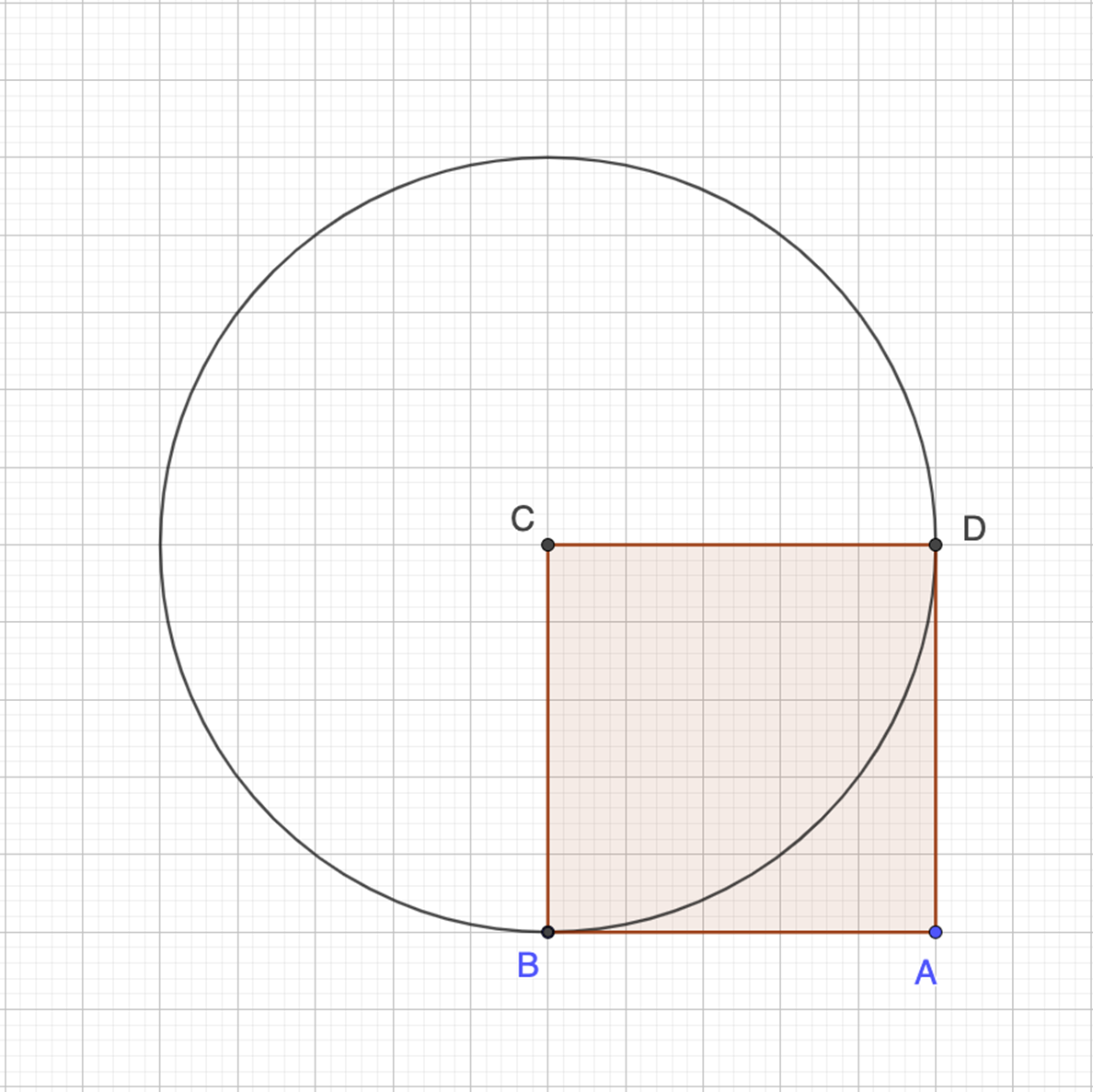
A continuación, observa al círculo y al cuadrado que se formaron en la imagen:
¿Cómo son el radio y el lado del cuadrado?
¿Qué relación tienen?
Formula tu respuesta.
La relación que hay entre el círculo y el cuadrado es que el radio del círculo y el lado del cuadrado miden 5 unidades.

Observa nuevamente la imagen para responder la siguiente pregunta:
¿Cuál es el área del cuadrado?
Se sabe que el perímetro es la medida del contorno de una figura dada en unidades lineales, y el área es la medida de una superficie comprendida dentro del perímetro de cualquier figura plana dada en unidades cuadradas.
Observa que el cuadrado está formado por 25 cuadrados que miden una unidad por lado, por lo tanto, su superficie es de 25 unidades cuadradas.

Así que el área del cuadrado es de 25 unidades cuadradas. No olvides este valor porque te será de utilidad más adelante.
En el círculo, al perímetro se le llama circunferencia y el área es la superficie dentro de la circunferencia.
Responde:
¿Cuál es el área del círculo?
Para determinar el área del círculo realiza una estimación razonable, con ayuda de la cuadrícula, contando los cuadrados que tomarás como unidad de medida.
Para ello, cuenta 64 cuadrados completos. Luego considera los cuadrados que son cortados por el círculo, y realiza “compensaciones” entre ellos.
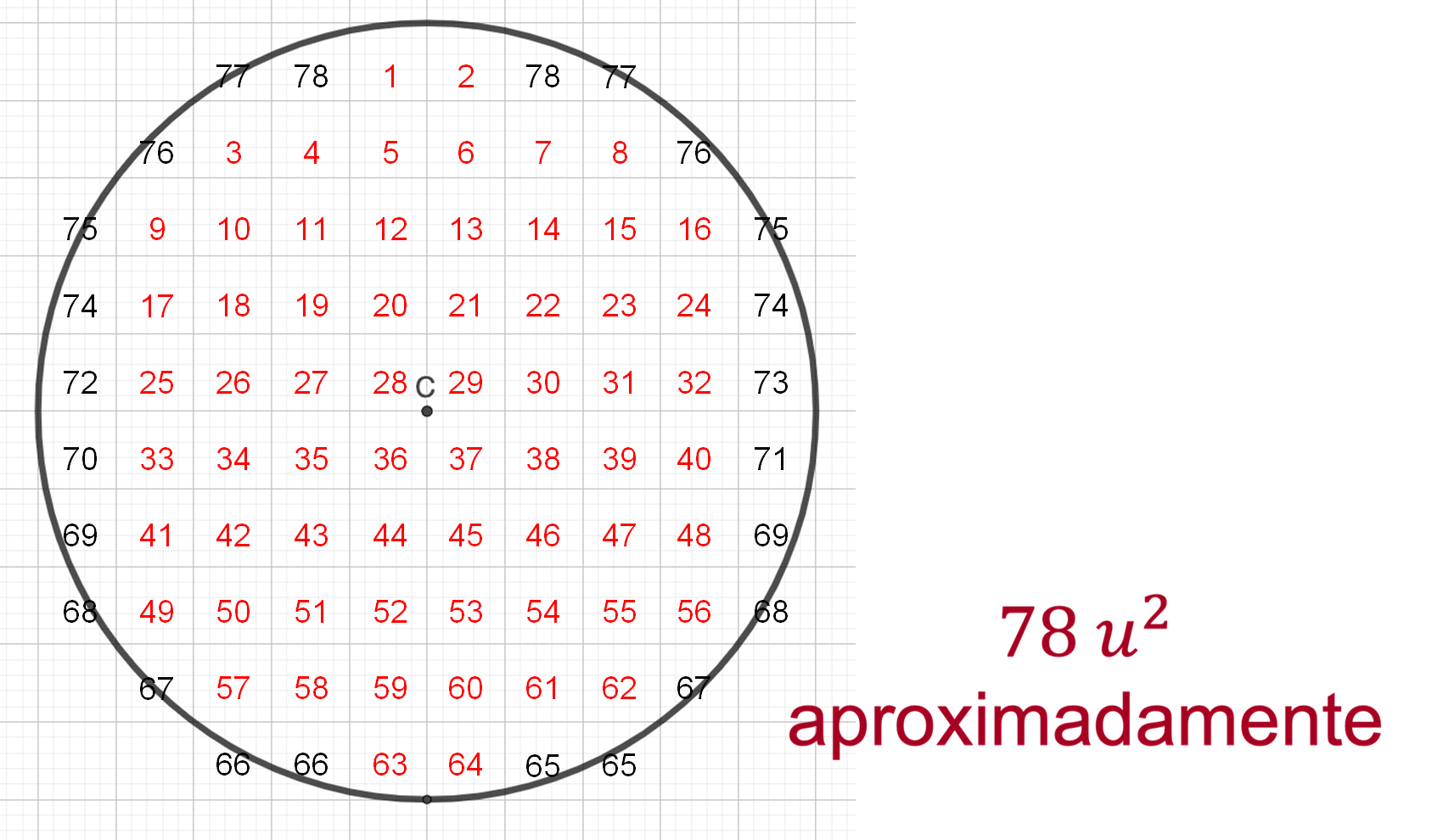
De esta manera, se puede decir que el círculo tiene una superficie aproximada de 78 unidades cuadradas, es decir, el área del círculo es de 78 unidades cuadradas aproximadamente.
Analicen de nuevo la imagen y trata de responder la siguiente pregunta:
¿Qué relación existe entre las áreas del cuadrado y del círculo, que tienen la misma medida de lado y radio, respectivamente?
Una forma de relacionarlos es planteando cuántas veces cabe una figura dentro de otra.
Responde:
¿Cuántas veces cabe el área del cuadrado dentro del área del círculo?
Para ello tienes que dividir 78 unidades cuadradas entre 25 unidades cuadradas.

Al dividir 78 unidades cuadradas entre 25 unidades cuadradas, tienes como resultado el cociente 3.12.
¿Qué representa este valor?
Es el número de veces que cabe el área del cuadrado dentro del círculo, es decir, el área del cuadrado cabe 3.12 veces dentro del área del círculo.
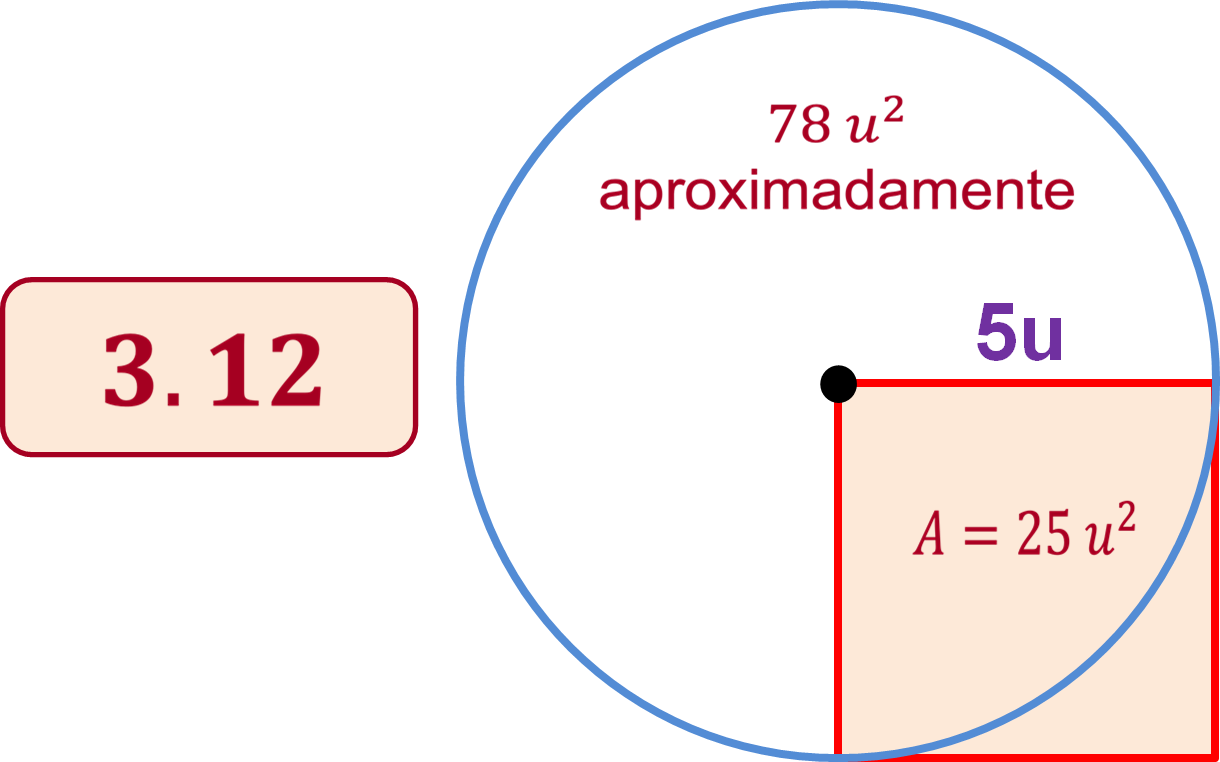
A continuación, resuelve la siguiente situación-problema, y responde:
- ¿Cómo se puede obtener el área de un círculo a partir de un cuadrado cuyo lado mide lo mismo que el radio del círculo?
Para responder, analiza lo que hizo Hilda, quien trabajó en un programa de Geometría dinámica, en su computadora.
Hilda, trazó dos círculos y dos cuadrados, los lados de los cuadrados miden lo mismo que los radios de sus círculos correspondientes. Después, midió con el programa de geometría dinámica, los lados de los cuadrados que son igual a los radios de sus círculos correspondientes y tienen un valor de 8 y 9.6 unidades, respectivamente. También mediante el programa determinó las áreas de ambos círculos, que son 201.06 y 289.529 unidades cuadradas, respectivamente.
Analiza las construcciones de Hilda.
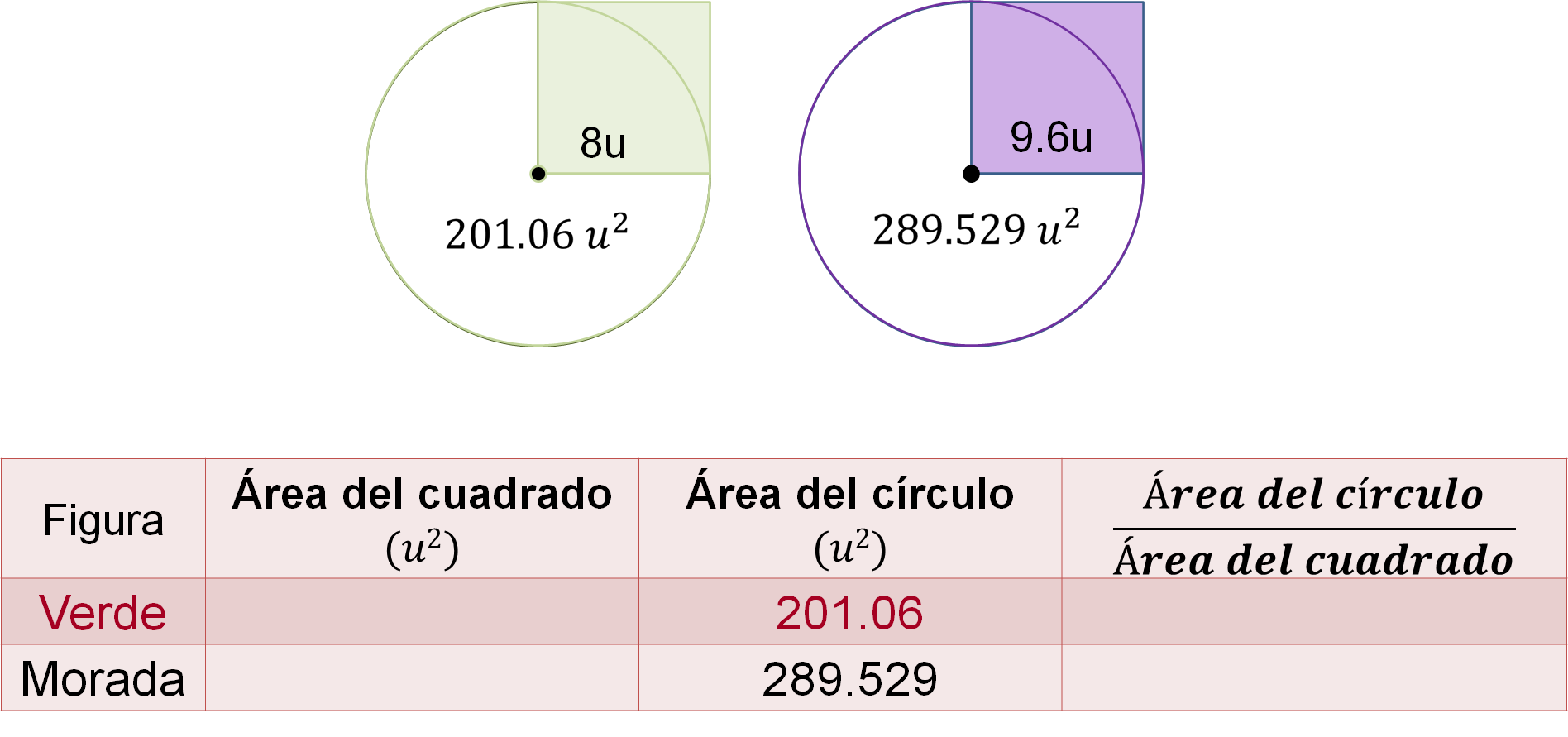
Observa la tabla: en la primera columna se indica la figura correspondiente, en la segunda columna se indica el área de los cuadrados, en la tercera columna se indica el área del círculo, y en la cuarta columna se indica la relación de las áreas; es decir, el número de veces que cabe el área del cuadrado en el área del círculo.
¿Cuál es el área del cuadro verde?
Para calcular el área del cuadrado partirás de la fórmula:
Área = lado por lado
Por lo tanto, para la figura verde, se tiene que el área es igual al producto de ocho unidades por ocho unidades; al realizar la multiplicación se obtiene que el área es igual a sesenta y cuatro unidades cuadradas.

En tu cuaderno, lleva un registro tabular, como el que se está usando.
Ahora, ¿cuál es el área del cuadro morado?
Para la figura morada se tiene que el área es igual al producto de 9.6 unidades por 9.6 unidades. Al realizar la multiplicación se obtiene que el área es igual a 92.16 unidades cuadradas.

Ahora sabes que el área del cuadro morado es de 92.16 unidades cuadradas.
Consideremos que:
- El área del cuadro verde es 64 unidades cuadradas, y
- el área del cuadro morado es de 92.16 unidades cuadradas.
Ahora, reflexiona en lo siguiente:
¿Cuántas veces cabe el área de cada cuadrado dentro de su círculo correspondiente?
Para determinar cuántas veces cabe el área del cuadrado dentro del círculo hay que dividir el área del círculo entre el área del cuadrado.
Para ello, resuelve la figura verde, donde el área del círculo es de 201.06 unidades cuadradas, entre el área del cuadro que es de 64 unidades cuadradas, dividiendo tienes el cociente de 3.1415.
Registra el valor obtenido en la tabla.

Para la figura morada tienes que el área del círculo es de 289.529 unidades cuadradas entre el área del cuadro que es 92.16 unidades cuadradas, dividiendo se obtiene el cociente 3.1415.
Registra el valor obtenido en la tabla.

Analiza lo siguiente:
¿Qué observas en los resultados de la cuarta columna?

Los resultados son iguales porque es una razón proporcional, ya que, al dividir el área del círculo entre el área del cuadrado, sin importar las dimensiones del cuadro y del círculo, siempre y cuando el lado y el radio sean iguales, se obtendrá como cociente: 3.1415, es decir un valor aproximado al valor del número “pi”.
El valor de “pi” no se puede representar con un número natural ni con una fracción, ya que es un número irracional, es decir, la parte decimal del valor de pi es infinita y no tiene periodo, y por cuestiones de practicidad, para realizar operaciones y hacer cálculos, por ejemplo, el área de un círculo; es suficiente redondear la parte decimal de “pi” a dos o cuatro cifras, es decir, 3.14 o 3.1416.
Por lo tanto, el área de cada cuadrado cabe, aproximadamente 3.14 o 3.1416 veces en su círculo correspondiente, es decir, el valor aproximado de “pi”.
Ahora, responde la pregunta planteada en la situación-problema:
¿Cómo se puede obtener el área de un círculo a partir de un cuadrado cuyos lados miden lo mismo que el radio del círculo?
Como observaste en los ejemplos anteriores, cuando los lados del cuadrado miden lo mismo que el radio de círculo, para conocer el área del círculo, basta multiplicar el área del cuadrado por 3.14 o 3.1416.
Ahora, considerando que el lado del cuadrado y que el radio del círculo, miden “r”, el área del cuadrado es igual a “r” por “r”, es decir, “r” cuadrada. Entonces para obtener el área del círculo, multiplica “r” cuadrada por 3.1416.
De esta manera queda definida la fórmula para calcular el área del círculo, como:
Área del círculo = pi por radio al cuadrado

A continuación, resuelve una situación-problema para aplicar lo aprendido.
Situación-problema 1
Lía y Berna recortaron cuatro círculos con diámetros diferentes, colocaron una cuerda sobre cada circunferencia, midieron la longitud de las cuerdas, y los datos obtenidos se registraron en la siguiente tabla.
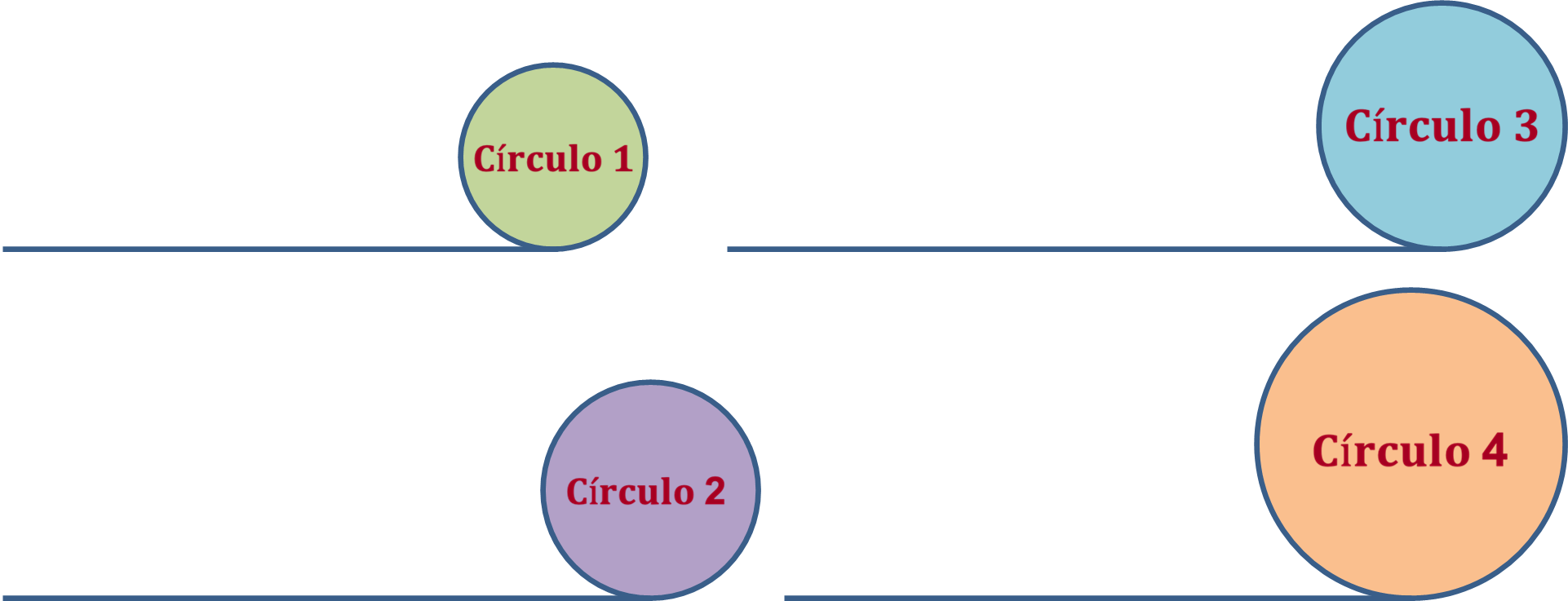
Los datos se registraron y se organizaron en la tabla de la siguiente manera:

En la primera columna se ubica el número asignado al círculo; en la segunda columna, la longitud de la circunferencia que se obtuvo al medir la longitud de la cuerda; en la tercera columna la longitud del diámetro y en la cuarta columna, la relación de la longitud de la circunferencia entre la longitud del diámetro.
Ahora completa la cuarta columna sustituyendo los valores en la relación, y al realizar cada operación registra cada resultado truncando hasta el orden de los diezmilésimos.

¿Qué significan estos resultados en el contexto de la situación-problema?
El cociente obtenido en la relación de la longitud de la circunferencia, entre la longitud del diámetro, significa el número de veces que cabe el diámetro en una circunferencia; por lo tanto, los valores obtenidos para los círculos 1, 2, 3 y 4 son muy cercanos al número pi, que como ya sabes, es aproximadamente 3.1416. Este número es una razón; ya que, al dividir el valor de la longitud de la circunferencia entre la longitud de su diámetro, para cualquier círculo, se aproximará a 3.1416.
El número “pi” tiene una cantidad infinita de cifras decimales y no tiene periodo. Para realizar operaciones se redondea “pi” a dos o cuatro cifras decimales, por lo tanto “pi” es aproximadamente igual a 3.1416.
Con base en lo anterior:
Si se conoce cuánto mide el diámetro de un círculo, ¿qué operación se debe hacer para calcular la longitud de la circunferencia?
Se sabe que la relación de la longitud de la circunferencia, entre el diámetro, es igual a “pi”.
Despejando, queda la expresión:
“Longitud de la circunferencia “lc” es igual a “pi” por la longitud del diámetro del círculo “ld”.
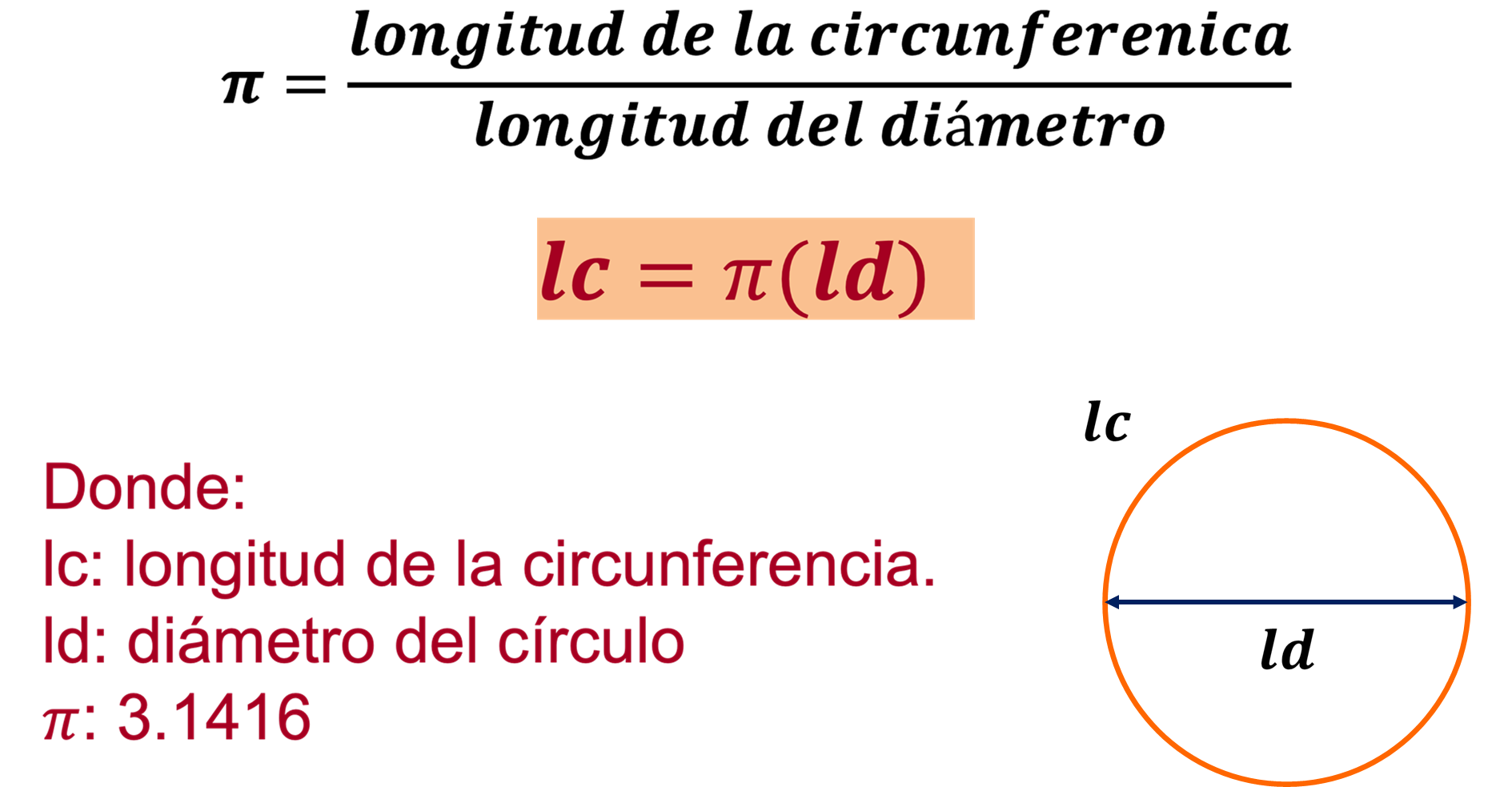
Por lo tanto, la operación para calcular la longitud de la circunferencia es una multiplicación.
Entonces, ¿cuál es la fórmula para calcular el perímetro de la circunferencia?
El perímetro es la longitud de la circunferencia, por lo tanto, se sustituye “lc” por “P”. Y la longitud del diámetro es simplemente el diámetro.
- “pi” es igual al perímetro entre el diámetro.
- Y “P” igual a “pi” por “d”, con el valor de pi aproximadamente igual a 3.1416.
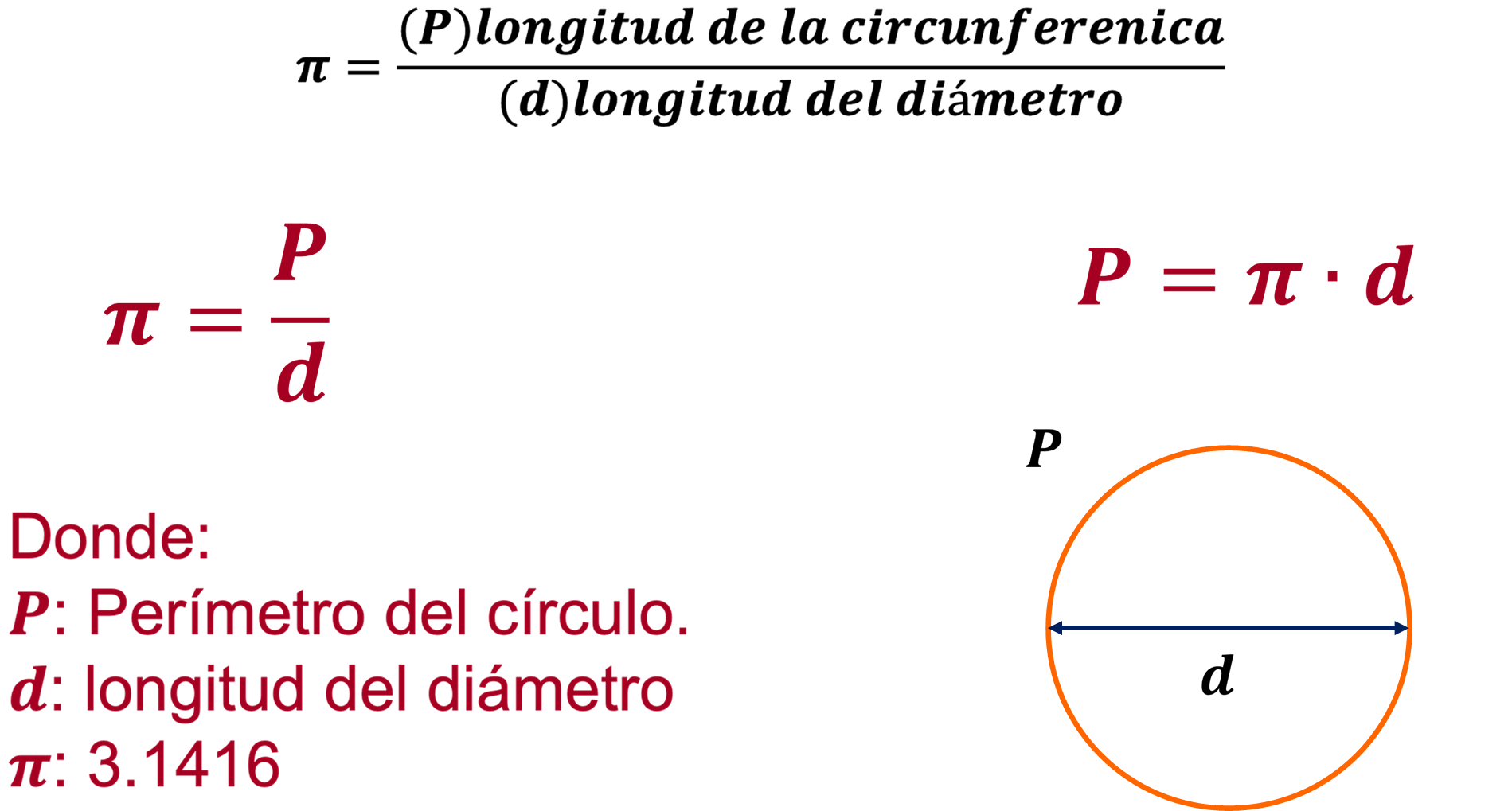
Por lo tanto, el perímetro de un círculo se calcula con la fórmula:
Perímetro = “pi” por diámetro.
Ahora ya conoces la expresión para calcular el perímetro de un círculo.
¿Cómo puedes calcular el perímetro de un círculo si sólo tienes el valor de su radio?
Se sabe que el radio es la mitad del valor del diámetro de un círculo; por lo tanto, sí se puede resolver cuando tienes como dato el radio. Lo multiplicas por dos, quedando la expresión:
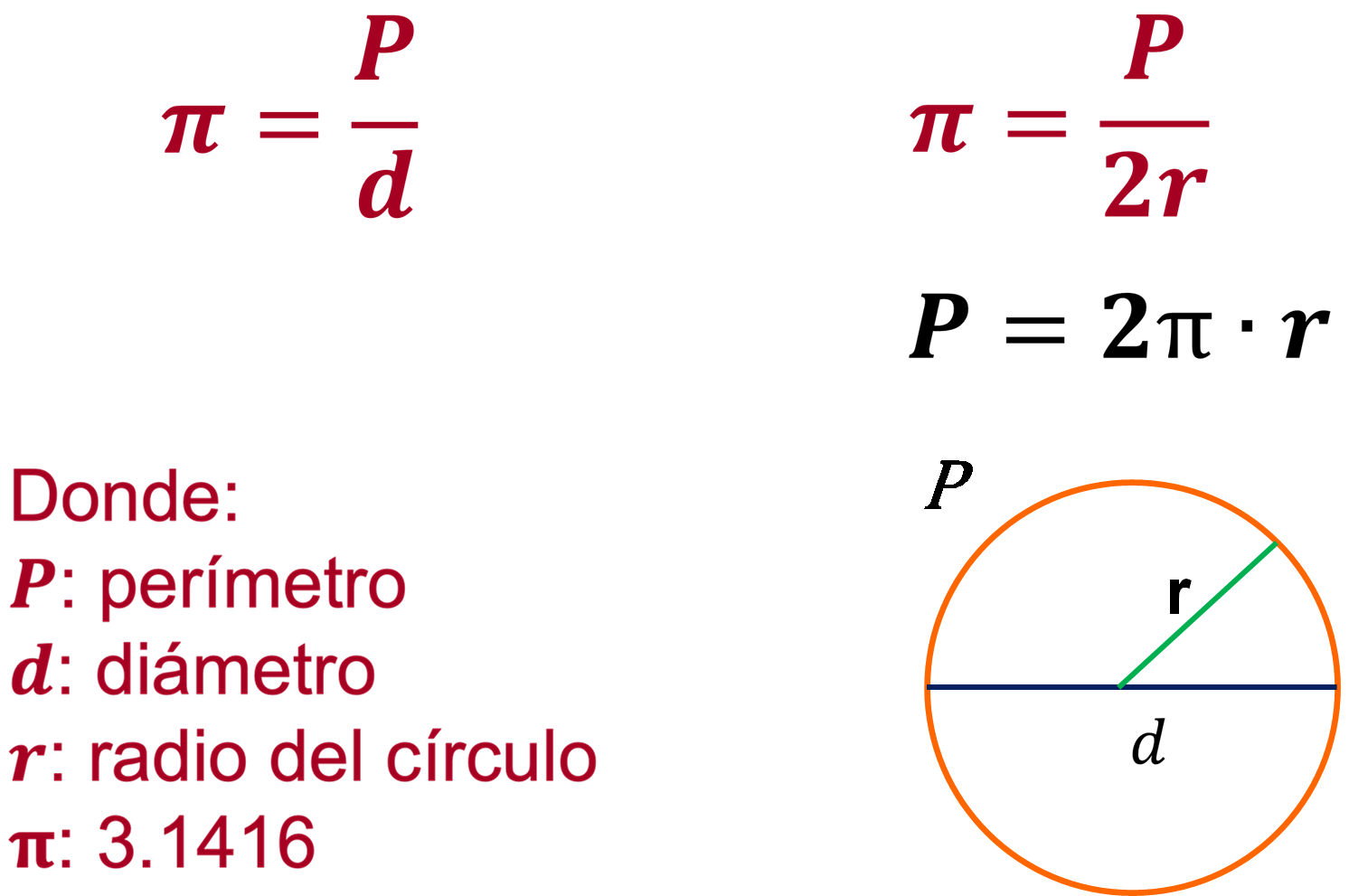
La fórmula para calcular el perímetro de un círculo si tienes el dato del radio es:
Perímetro = 2(pi) por radio
De esta manera quedan definidas las fórmulas para calcular el perímetro y el área del círculo, como:
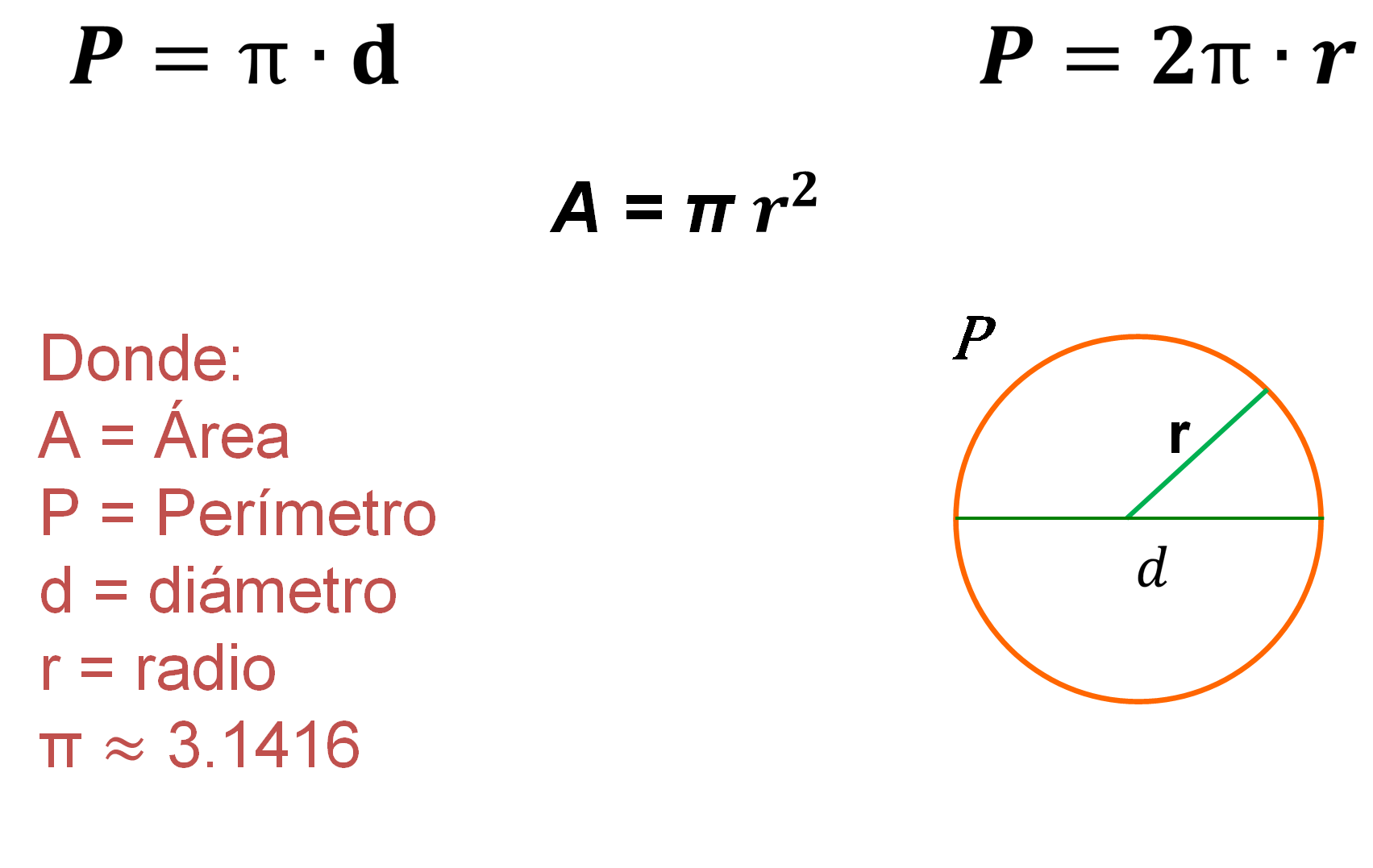
- Perímetro = pi por diámetro.
- Perímetro = 2(pi) por radio.
- Área = pi por radio al cuadrado.
Para aportar a estos conocimientos, resuelve la siguiente situación-problema relacionada con el perímetro y el área del círculo.
Situación-problema 2
Se requiere colocar un carrusel en una superficie circular. El área de la base del carrusel mide 50.24 metros cuadrados. Por seguridad se requiere que el espacio donde se va a colocar tenga 1.2 m más de cada lado del perímetro del carrusel, como se muestra.
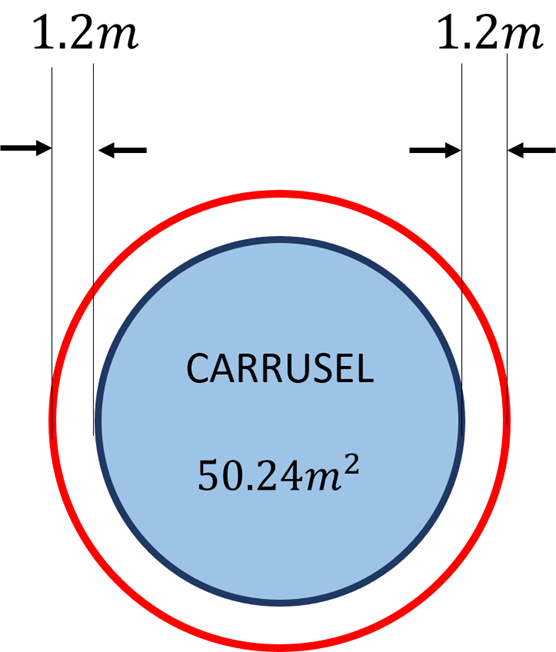
¿Cuánto debe medir el área de seguridad donde se quiere colocar el carrusel?
Se sabe que el círculo azul representa el área de la base del carrusel, y la circunferencia roja delimitará el área que se requiere para instalar el carrusel.
Primero responde:
¿Cuál es el diámetro del carrusel?
Partiendo de la fórmula para calcular el área del círculo: Área es igual a pi por radio al cuadrado, sustituye el valor del área en la expresión, y queda:
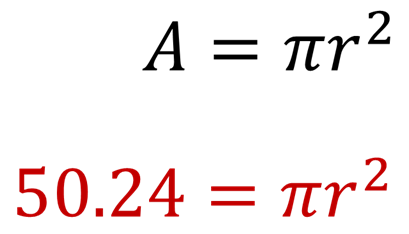
Despeja a “r” cuadrada. Para ello, “pi” que está multiplicando a “r” cuadrada, pasará a la izquierda dividiendo, quedando:
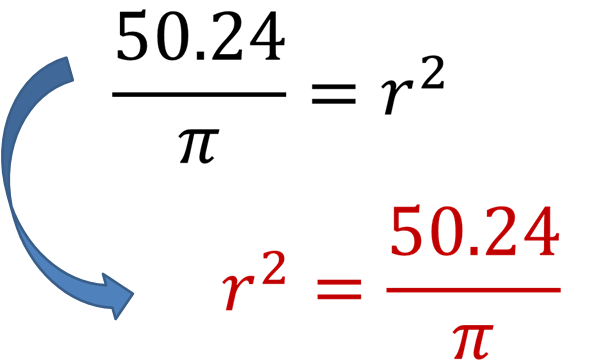
Una de las propiedades de la igualdad dice que, la operación que realices en un lado de una igualdad también tienes que hacerla del otro lado de la igualdad. Así que, como el radio está elevado al cuadrado, a ambos lados de la igualdad les extraes la raíz cuadrada, para obtener a “r”, ya que la operación inversa de elevar al cuadrado es aplicar la raíz cuadrada.
De esta forma, obtienes la expresión:

Dividiendo 50.24 entre pi tienes 15.99, y este lo aproximas a 16.
Tienes entonces que:

Puedes usar una calculadora y encontrarás que la raíz cuadrada de 16 es igual a 4. Porque la raíz cuadrada de un número, en este caso de 16, significa encontrar otro, que es 4, que multiplicado por sí mismo da 16.
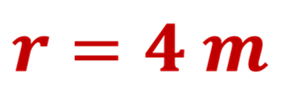
Así que el radio tiene un valor de 4 metros.
¿Qué representa este valor en el contexto del problema?
Este valor, representa el radio de la base circular del carrusel.
Ahora es necesario saber:
¿Cuál es el diámetro de la base del carrusel?
Se determina que el radio de la base del carrusel es r = 4 metros y como el diámetro es dos veces el radio, queda la expresión:
d = 2(r)
Sustituyendo tienes que:

Por lo tanto, el diámetro de la base del carrusel es igual a 8 m.
Continúa con el problema.
El diámetro de la base del carrusel es de 8 metros, al cual le sumarás el doble de 1.2 metros, que representará el diámetro del círculo cuya área que se requiere para instalar el carrusel por seguridad.
Por lo tanto, queda la expresión:
d = 8m + 2(1.2m)
Efectuando la multiplicación y sumando las cantidades, queda:
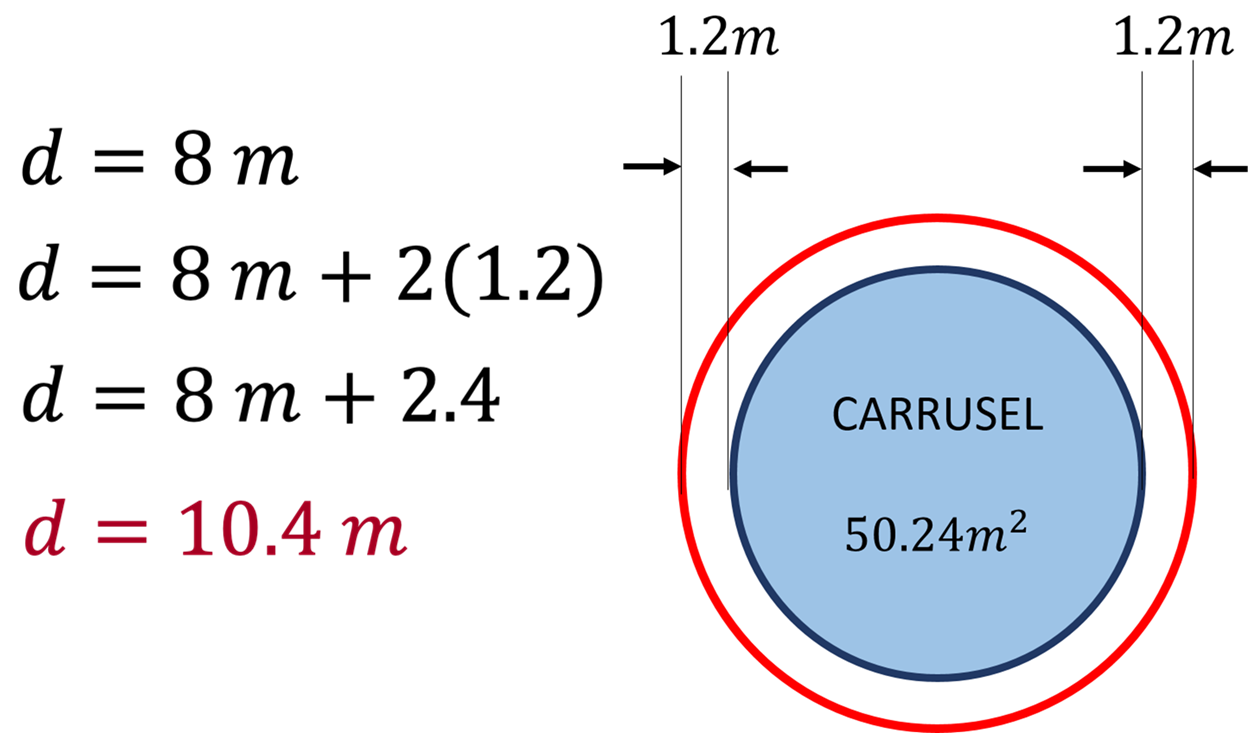
Entonces, el diámetro del círculo de seguridad es de 10.4 m.
¿Qué representa este valor en el contexto del problema?
Este valor, representa el diámetro del área que se requiere para instalar el carrusel.
Ahora, calcula el valor del área del círculo de seguridad que se requiere para instalar el carrusel.
Para ello, partirás con el cálculo del radio, mediante la expresión:
Radio = diámetro entre 2
Sustituyendo, tienes que:
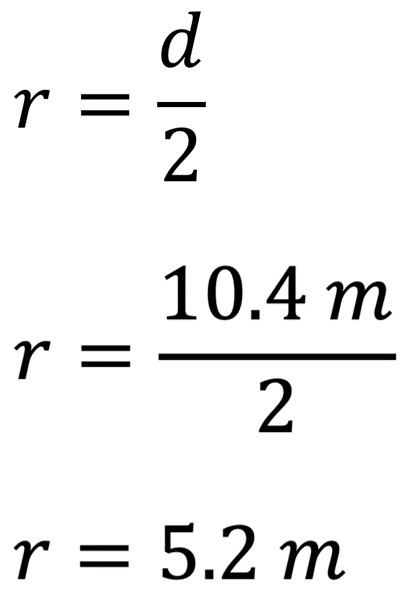
Ahora, calcula el área total de seguridad que se requiere para instalar el carrusel, con la expresión:
Área = Pi por radio al cuadrado
Sustituyendo valores, tienes:
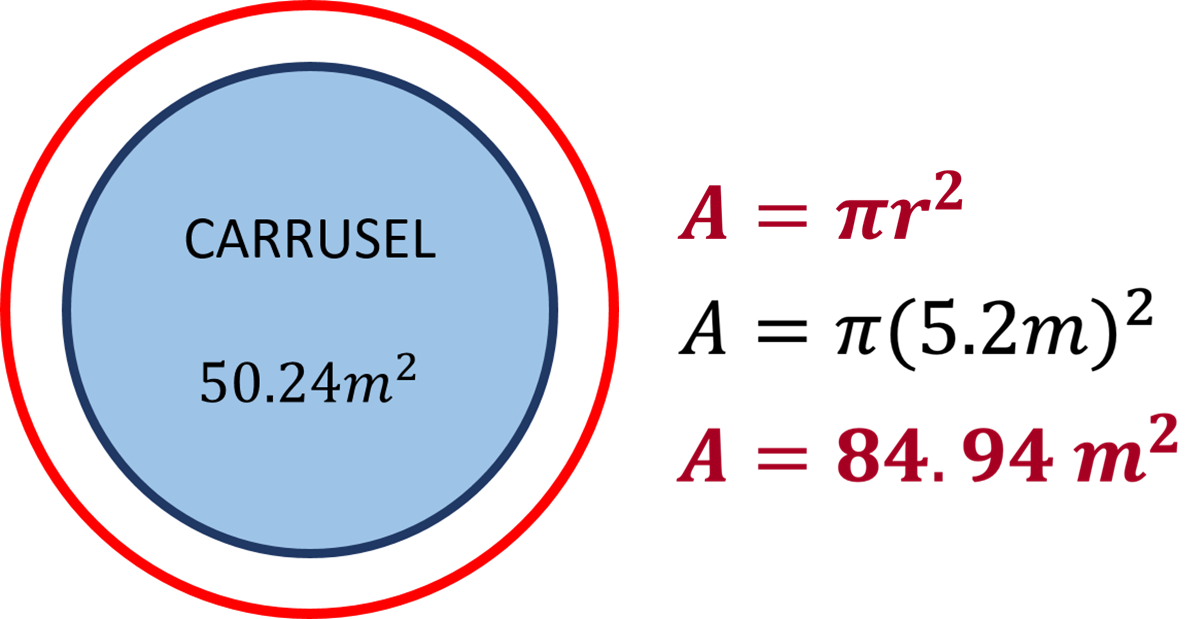
Por lo tanto, el área requerida para instalar el carrusel es de 84.94 metros cuadrados.
Has resuelto la situación planteada.
En esta sesión, estudiaste las fórmulas para calcular el área y el perímetro del círculo, y usaste dicha fórmula para la resolución de una situación-problema.


No hay comentarios.:
Publicar un comentario