terceros años
27/10/2020
Desarrollo del binomio al cuadrado I
Aprendizaje esperado: Resuelve problemas que implican el uso de ecuaciones de segundo grado.
Énfasis: Resolver problemas cuadráticos usando factorización.
¿Qué vamos a aprender?
Darás continuidad al tema sobre la resolución de problemas que involucran a las ecuaciones cuadráticas.
En caso de que no cuentes con tu libro, tienes la opción de consultarlo a través de la página de la Comisión Nacional de Libros de Texto Gratuitos.
Procura recrear en tu cuaderno las figuras y las soluciones que aprenderás.
No olvides registrar tus dudas, inquietudes y anotaciones respecto a esta lección.
Empieza recordando cómo se resuelve el producto de dos binomios con un término común.
Por ejemplo, resuelve el siguiente producto de binomios con un término común:
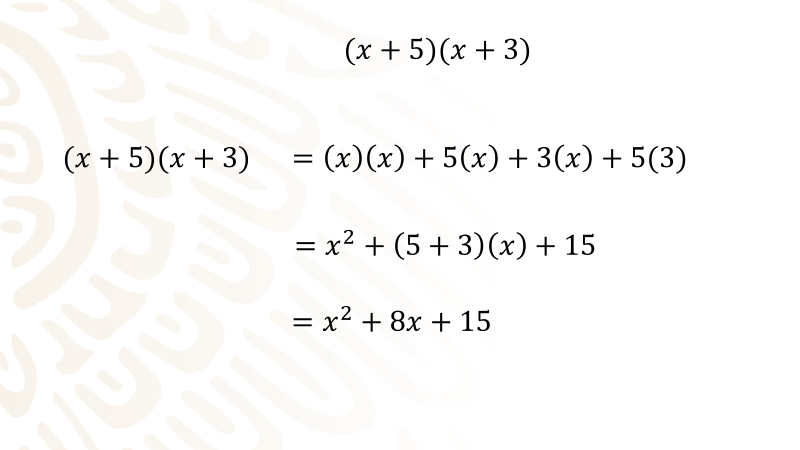
Primero multiplicas el primer término “x” del primer binomio por los dos términos del segundo binomio y queda: (x) (x) + (x) (3) = 3x.
Ahora multiplica el segundo término del primer binomio, 5, por los dos términos del segundo binomio:
(5) (x) = 5x, (5) (3) = 15
La expresión que queda es: x^2+3x+5x+15
(x)(x) = x^2
Reduces términos semejantes: 3x+5x= 8x, por lo cual te queda el trinomio: x^2+8x+15
A partir del ejemplo anterior contesta las siguientes preguntas:
- ¿Cómo se obtiene el término cuadrático?
- ¿Cómo se obtiene el término lineal?
- ¿Cómo se obtiene el término independiente?
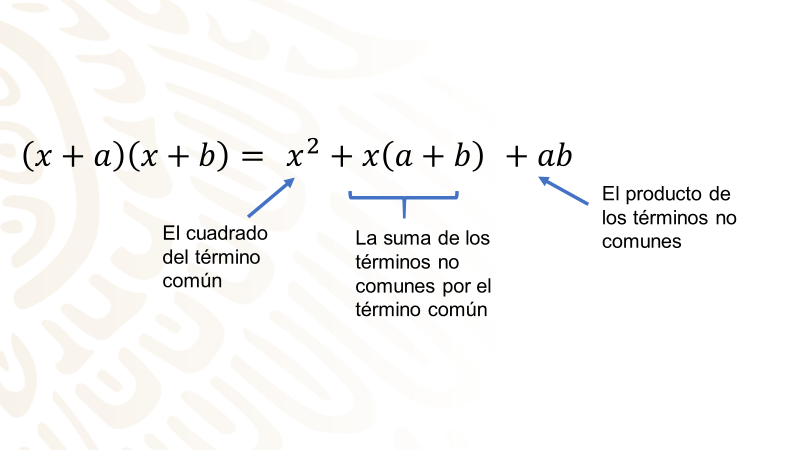
Te diste cuenta que puedes llegar a una simple regla para desarrollar el producto de dos binomios con un término común y la puedes enunciar de la siguiente manera:
“El producto de dos binomios con un término común es igual al cuadrado del término común, más la suma de los términos no comunes por el término común, más el producto de los no comunes”.
Ahora aplicarás esta regla al siguiente producto de binomios con un término común: (x+6) (x+4)
Primero identifica los términos comunes: “x”, ya que es el termino común en ambos binomios. Identifica los términos no comunes. Los términos no comunes son 6 y 4.

Ya identificados los términos no comunes y el término común, aplica la regla:
El producto de dos binomios (X+6) (X+4) es igual al cuadrado del término común x^2,
más la suma de los términos no comunes por el termino común (6+4) x, más el producto de los no comunes (6)(4)
Por lo cual quedaría de la siguiente manera: (x+6) (x+4) = x^2+10x+24
¿Qué hacemos?
Consolida como resolver el producto de binomios con un término común con el siguiente video del minuto 5:39 al 9:27:
- Resolución de ecuaciones cuadráticas expresadas en su forma general
https://www.youtube.com/watch?v=sqJFpeXVIKo
Observa algunos problemas relacionados. De los cuadriláteros A, B, C, y D, observa las medidas de cada uno de ellos.
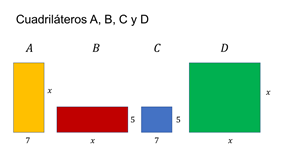
Forma un rectángulo al que llamarás figura E.

¿Cómo obtienes el área de un rectángulo? El área de un rectángulo es el producto de su base por su altura. Obtén su base y su altura.
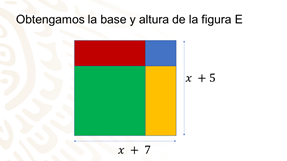
La base está formada por el cuadrado con lado x y el rectángulo de base 7, entonces la base mide x + 7. La altura será entonces la suma de la altura del rectángulo A que es x más la altura del rectángulo C, que es 5. Entonces la altura de la figura E será x + 5.
Por lo tanto, área de la figura E = (x+7) (x+5)

Como observas son dos binomios con un término común. Por lo que puedes aplicar la regla ya mencionada:
Entonces (x+7) (x+5) al cuadrado del término común x^2, más la suma de los términos no comunes por el termino común (7+5) x, más el producto de los no comunes (7)(5).
Por lo cual quedaría de la siguiente manera: (x+7) (x+5) = x^2+12x+35
Observa otro ejemplo:
El caso de Samuel, que vive en una pequeña comunidad al sur del Estado de Coahuila, donde tienen a lo largo del año, muchos días soleados.
Samuel estudia el tercer grado de secundaria y le gustan las matemáticas, la astronomía y últimamente está interesado en las energías renovables, y sabe que se puede transformar la radiación solar en energía eléctrica utilizando paneles solares. Le propone a su padre instalar paneles solares en la casa. Así, compran 8 paneles solares de diferentes tamaños.
Observa los paneles y observa sus medidas.

Samuel y su padre ensamblan los paneles de tal manera que forman un rectángulo que será capaz de colectar radiación solar de manera más eficiente.

¿Cuánto mide el ancho del rectángulo formado por los ocho paneles solares?
El ancho mide x+1.

¿Cuánto mide el largo del rectángulo formado por los ocho paneles solares?
El largo mide x + 3.
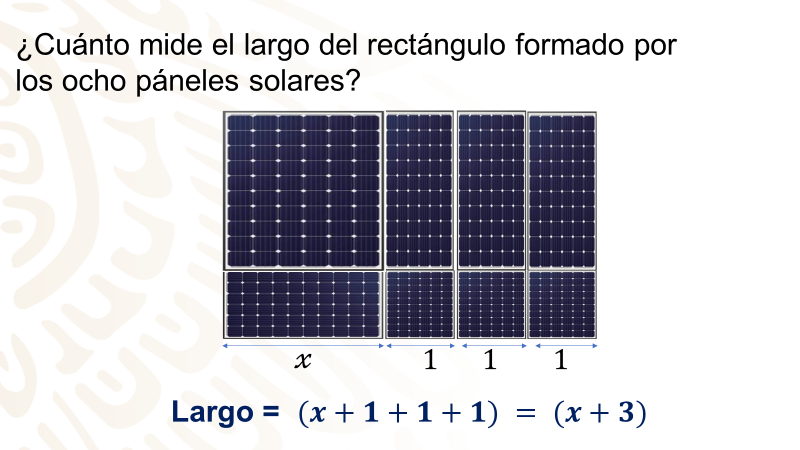
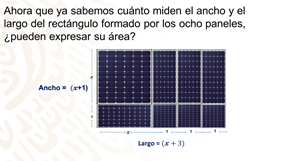
Ahora que ya sabes cuánto mide el ancho y el largo del rectángulo formado por los ocho paneles ¿puedes expresar su área?
El área total del panel formado por las 8 piezas es igual a la base por la altura, es decir: (x+1) (x+3)
Aplicando la regla, se obtiene que:
x^2 + x (1+3) +(3) (1)
Por lo tanto, el área total del panel formado por las 8 piezas es igual a: x^2 + 4x + 3.

¿Será la suma de las áreas de los 8 paneles individuales igual al área total de los 8 paneles juntos? Verifícalo.
Ahora considera el caso donde debes encontrar los binomios con factor común.
Comienza con la siguiente situación:
Don Juan es fabricante de vitrales y su hijo Pedro que le ayuda en su negocio se encuentra estudiando el 3er grado de secundaria.
En una ocasión Don Juan tuvo que salir dejando encargado el negocio a su hijo Pedro, le pidió que fuera avanzando en la construcción del vitral como se muestra en la figura, pero sólo le dejó como medida del área total la siguiente expresión: x²+13x+40.
¿Puedes ayudar a Pedro a encontrar la expresión que represente las medidas de este vitral?

Recuerda cómo se factorizan este tipo de expresiones. Observa que es un trinomio de segundo grado o cuadrático.
Comienza a resolverlo: x²+13x+40
Descompón el trinomio en dos factores binomios cuyo primer término será la raíz cuadrada del primer término. ( ) ( )
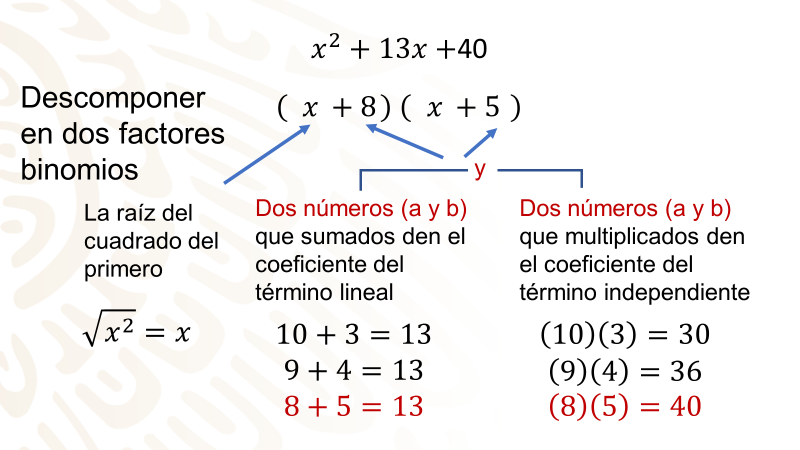
¿Cuál es esa raíz? Raíz cuadrada de x^2 = x
Esta raíz se coloca en ambos paréntesis: (x ) (x )
Ahora busca dos números que sumados den como resultado 13, para el término lineal y que multiplicados den como resultado 40, el término independiente.
¿Cuáles son esos dos números? Si buscas esos números que sumados den como resultado 13, pueden ser 10 y 3, o el 9 y el 4, el 8 más 5, entre otros.
Estos dos números multiplicados deben dar resultado el término independiente que es 40. De las parejas mencionadas, la única que satisface esta condición es la formada por 8 y 5.
Sólo falta considerar los signos. Si observas en el trinomio todos son positivos por lo cual la factorización quedaría de la siguiente manera. (x+8) (x+5)
Don Juan felicitó a Pedro por los avances de su trabajo.
En el siguiente video del minuto 9:36 al 12:39, considera un caso más.
- Resolución de ecuaciones cuadráticas expresadas en su forma general
https://www.youtube.com/watch?v=sqJFpeXVIKo
Los problemas que has visto se refieren a la obtención de áreas. ¿En dónde más puedes aplicar este método de factorización?
También puedes aplicar este método de factorización para realizar algunos cálculos. Observa el siguiente caso:
A Lupita le encanta el cálculo mental y su maestra le propone el siguiente reto:
¿Puedes obtener el resultado de multiplicar 18 por 14 utilizando el producto de
dos binomios con un término común?
Lupita rápidamente analiza lo siguiente
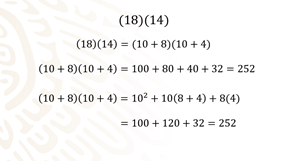
18 se puede descomponer como 10 + 8 y 14 como 10 +4.
Ambos como tienen como factor común al número 10. Ahora, multiplicando estos dos factores
(10+8) (10+4) = 100+80+40+32 = 252
Pero, siguiendo la regla que aprendiste: (10+8) (10+4) = 10^2 + 10(8+4) + 8(4)
Haciendo los cálculos: (10+8) (10+4) = 100+120+32 =252.
Observa un caso un poco más complicado: (121) (103)

Esto puede descomponerse de la siguiente forma:
(121) (103) = (100 + 21) (100 + 3)
Siguiendo la regla (100 + 21) (100 + 3) = 100^2 + 100(21+3) + 21(3)
Haciendo los cálculos: = 10000 + 2400 + 63 = 12,463
Observa el último caso y ocupa decimales (10.1) (10.5)
Ahora descompón los factores de la siguiente forma:

(10.1) (10.5) = (10 + 0.1) (10 + 0.5)
Siguiendo la regla: (10 + 0.1) (10 + 0.5) = 10^2 + 10 (0.1+0.5) + (0.1) (0.5)
Haciendo los cálculos: (10 + 0.1) (10 + 0.5) =100 + 10 (0.6) + 0.05
(10 + 0.1) (10 + 0.5) = 100 + 6 + 0.05 = 106.05


No hay comentarios.:
Publicar un comentario