terceros
26/10/2020
Producto de dos binomios con un término común
Aprendizaje esperado: Resuelve problemas que implican el uso de ecuaciones de segundo grado.
Énfasis: Resolver problemas cuadráticos usando factorización.
¿Qué vamos a aprender?
Has estado trabajando en resolver problemas de ecuaciones cuadráticas a través de la factorización.
Continuarás fortaleciendo la técnica de factorizar expresiones en los binomios conjugados.
Centra tu atención a cada uno de los problemas que se resolverán, la idea es que, con ellos, se apoye tu habilidad de planteamiento y resolución de problemas que se pueden resolver mediante el planteamiento de ecuaciones de segundo grado.
¿Qué hacemos?
Inicia con el primer problema matemático de esta sesión.
Jaime es dueño de un terreno de forma cuadrangular de 10,000 m2. Hace unos días, el municipio le dice que para urbanizar el pueblo requieren hacer modificaciones a su propiedad, pues van a trazar una calle en la parte norte de su terreno. Le dicen que le van a quitar una franja de 5 metros al ancho de su terreno. Para ello le ofrecen compensarlo, en la parte ESTE de su propiedad, con una franja de 5 metros de ancho, hasta el nuevo límite que tendrá el resto del terreno en la parte NORTE.
Revisa si la situación le será favorable a Jaime.
Trabaja ahora las expresiones del problema. Puedes igualarla a cero para resolver la ecuación de segundo grado que se genera del siguiente modo:

Si utilizas la factorización de la expresión anterior, puedes obtener por factorización del primer miembro, lo siguiente:
x^2 – 10000 = 0
Obtienes la raíz cuadrada de equis al cuadrado y la raíz de 10000. Una vez que obtienes la raíz cuadrada queda: “x” y 100. Forma ahora dos binomios conjugados con los términos encontrados y obtienes:
(x+100) (x-100) = 0
Recuerda que se llaman binomios conjugados debido a que sólo se diferencian por tener signos contrarios, es decir, uno de los factores es una adición y el otro una sustracción. Para que la ecuación sea igual a cero, se necesita que uno de los factores o los dos sean cero.
Entonces, iguala a cada uno de los factores a CERO y resuelve la ecuación que se forma en cada caso:

Toma aquí la solución positiva de la ecuación, ya que el lado de un cuadrado en un terreno no puede ser negativo.
Así sabes que la medida del lado del terreno es de 100 metros.
Relaciona ahora lo anterior con el área total del terreno de Jorge, usando expresiones algebraicas.
Observa el área total disminuida en la zona norte se puede representar como:

Por lo que, esta expresión representa que, al terreno original de Jaime, le van a disminuir 25 metros cuadrados. Por lo tanto, no le conviene el trato con el municipio, lo que puedes verificar factorizando la expresión anterior.
Tienes:
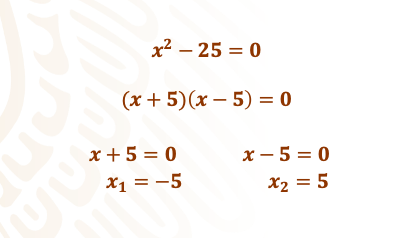
Lo que al final demuestra el aumento y la disminución del área del terreno de Jaime.
Lo importante es que, en este caso, has podido saber con planteamientos matemáticos si le conviene a Jaime o no hacer un acuerdo con el ayuntamiento.
Ahora resuelve un problema que en sí mismo es sencillo, pero usarás la factorización por binomios conjugados como forma de solución. Seguro podrás encontrar otra manera de resolverlo.
Tienes una situación que resolverás matemáticamente, pues hacerlo de manera personal sería muy complejo ya que requeriría movilizar a muchas personas.
Se quiere distribuir a las 784 personas, que forman una compañía militar, en una formación con igual número de columnas y filas para una presentación en la plaza principal de un poblado, ¿cuántas personas habría en cada una de ellas?
Recuerda que puedes aprender varios métodos para resolver ecuaciones de segundo grado.
Ahora, resuelve el siguiente problema:
Don Juan es herrero y recibe el encargo de fabricar el marco de un espejo para un cliente muy peculiar, Don Fabián. Don Fabián desea un marco metálico hecho en una sola pieza, por lo cual, sólo debe recortarse de su interior, el espacio en donde irá el espejo. Le hace llegar a Don Juan, las indicaciones exactas para que lo construya:
Instrucciones para elaborar el marco:
- Debe recortar la parte donde irá el espejo a partir de una sola pieza.
- Dicha parte es un cuadrado que tiene de área 1071 centímetros cuadrados, y el largo está representado por (x + 15) y el ancho (x – 15).
- El ancho de dicho marco debe medir 8 cm de cada lado.
Observa las especificaciones:
- la zona interior es el espejo y el área de ésta es de 1071 centímetros cuadrados.
- su ancho está representado por x-15 y la base por x+15.
Para que Don Juan elija la placa metálica que va a necesitar, investiga y se da cuenta que las venden en forma de cuadrado en los siguientes tamaños:
- 60X60
- 70X70
- 75X75
- 80X80 centímetros
Ayuda a Don Juan a saber cuál debe comprar. Plantea la expresión que corresponde para calcular el área del espejo, lo que lograrás multiplicando la base por la altura ya que se trata de un rectángulo.
Tienes la expresión: (x+15) (x-15) = 1071. Multiplicas los factores e igualas a cero, teniendo: x^2 - 225=1071
Añade 1071 negativo a ambos miembros de la igualdad. Y reduce teniendo: x^2 – 1296 = 0
Ahora factoriza para resolver: x^2 – 1296 = 0
Obtiene la raíz cuadrada de ambos términos, así la raíz cuadrada de x^2 es “x”. Y la raíz de 1296, que es 36.
Forma los binomios conjugados: (x+36) (x-36) = 0
Y resuelve: (x+36) (x-36) = 0
Del primer factor obtienes: x+36=0 x subíndice 1 igual a 36 negativo
Del segundo factor tienes: x-36=0 x subíndice 2 igual a 36.
De las soluciones que encuentras, tomas la que es positiva y a partir de ahí, observa que, si x = 36, las medidas del espejo se obtienen de la siguiente forma:
En la altura se resta a los 36 cm, 15 cm y obtienes 21. Y en la base, a los 36 le sumas 15 cm y obtienes 51. Ahora, el área solicitada es verificable si multiplicas 21X51 que es igual a 1071 centímetros cuadrados.
Ahora, a Don Juan le has apoyado a calcular las dimensiones del espejo, falta, ahora, saber las dimensiones del marco. Para ello, recuerda que, en las instrucciones, Don Fabián especificó que debería medir 8cm de cada lado, así tienes que las dimensiones del marco del espejo quedarán así:
8 cm para cada parte del marco y en la altura del espejo, que es de 21 cm, tienes en total: 21+8+8=37 cm. Y en la base tienes: 51+8+8=67 cm.
Recuerda los diferentes tamaños de las placas de metal que puede adquirir, éstas son de:
60X60
70X70
75X75
80X80 cm
Partiendo de ello y que el marco completo debe medir 37x67 cm, la placa que le conviene elegir es la de: 70x70. Esta placa le alcanza para recortar el marco en una sola pieza y es en la que menos material desperdicia Don Juan para elaborarlo.
Ahora Don Fabián puede tener el marco para su espejo como lo desea, de una sola pieza.
Ahora, ayuda a Jorge a encontrar la medida de una rampa de carga a escala, que debe construir para su clase de física. La va a construir con tiras de madera. Lo que sabe es que, vista de forma lateral, forma un triángulo rectángulo. Su profesor de Física le indica que va a manejar el modelo a escala. Entonces, el profesor le entrega el siguiente esquema.
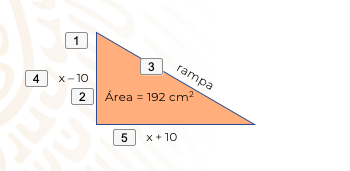
Como notarás, el triángulo rectángulo tiene de base (x + 10) centímetros y de altura (x - 10) centímetros, y debe tener de área 192 centímetros cuadrados.
centímetros, y debe tener de área 192 centímetros cuadrados.
Como la idea es construir la rampa, debes saber cuánto debe medir cada una de las tiras de madera que son el armazón de la rampa, así que debes encontrar primeramente cuánto mide la base y la altura.
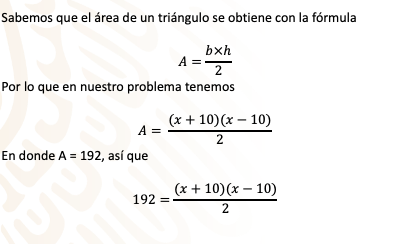

Factorizando, tienes:

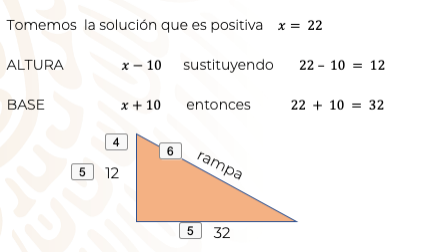
Y aquí ves el triángulo y sus medidas.
Ahora, la rampa que Juan tiene que construir tendrá de base 32 centímetros y de altura 12 centímetros, sólo falta calcular la hipotenusa del triángulo rectángulo, pues es precisamente ésta, la que es la parte deslizable de la rampa.
Si quieres calcular la hipotenusa, la parte deslizable de la rampa, puedes usar un teorema muy útil, el teorema de Pitágoras.
Mediante este teorema, tienes que:
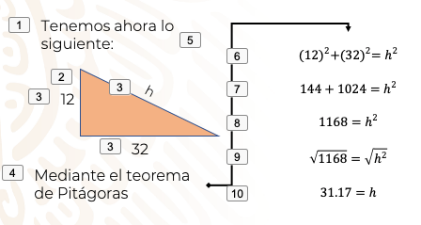
Como ves, la rampa mide 34.17 cm, has logrado calcular esta distancia utilizando el teorema de Pitágoras que, como recordarás, es muy útil cuando se tienen triángulos rectángulos.
Ahora sí, Jorge tiene todas las medidas que requiere para construir su rampa.
En todos los problemas vistos, has factorizado expresiones llamadas “diferencias de cuadrados” y obtienes de ellos “binomios conjugados”.
En todos los casos tienes ecuaciones cuadráticas, mismas que tienen dos soluciones y, en este caso en particular, son simétricas. Has resuelto varios problemas en contextos diversos.


No hay comentarios.:
Publicar un comentario