primeros años 27/11/2020 Transformando ecuaciones

 

primeros años

27/11/2020

Transformando ecuaciones

Aprendizaje esperado: Resuelve problemas mediante la formulación y solución algebraica de ecuaciones lineales.

 

Énfasis: Reducir términos semejantes.

 

 

¿Qué vamos a aprender?

 

Ya has revisado diferentes formas de ecuaciones lineales, donde la incógnita puede ser representada por medio de una literal (que puede ser cualquier letra del alfabeto).

 

En esta sesión estudiarás otras formas de ecuaciones que incluyen el uso de paréntesis, y con ello utilizarás las distintas propiedades de los números y las operaciones que ya has trabajado, éstas te permitirán transformar las ecuaciones reduciendo sus términos semejantes. También estudiarás los elementos que conforman un término algebraico.

 

 

¿Qué hacemos?

 

Observa el siguiente término algebraico:

 

 

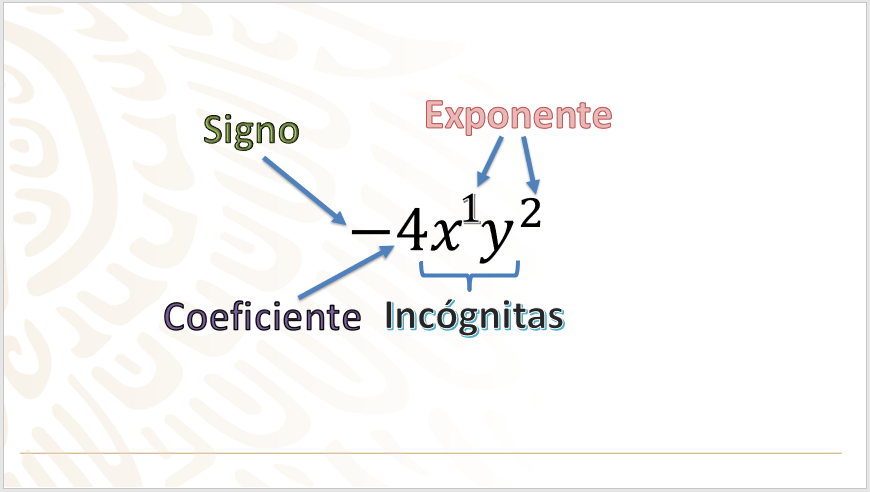
Los elementos que lo conforman son: el signo, que en este caso es negativo; el coeficiente, en este caso es el número 4; las literales, en este ejemplo son dos: “x” y “y”; y por último los exponentes, “x” tiene exponente a la potencia 1, porque cualquier valor elevado a la potencia 1 es simplemente el mismo valor, que podemos no escribir, y “y” con exponente 2 o elevado al cuadrado.

 

Los términos semejantes son aquellos que tienen las mismas literales con los mismos exponentes sobre cada una de ellas, aunque las literales se encuentren en distinto orden y aunque los coeficientes sean diferentes, estos términos determinarán si se adicionan o sustraen, en álgebra.

 

Para comprenderlo a detalle. Imagina que se tiene una canasta con manzanas y peras. Si se separan por el tipo de fruta; podrían acomodarse del lado derecho, exclusivamente las manzanas, y del lado izquierdo las peras, lo que quiere decir que se están separando los términos semejantes, es decir, que se están separando los elementos por sus características. Lo mismo sucede con los términos algebraicos, éstos se pueden simplificar o reducir si tienen la misma literal y exponente, sin importar su coeficiente.

 

SI una persona decide vender peras y manzanas por unidad; es decir, vende cada manzana independientemente, y cada pera también. Representemos cuánto se pagaría por las peras usando un término algebraico, enseguida representemos el precio de las primeras 3 peras del primer grupo. Asociando “3p” al primer conjunto donde el 3 representa la cantidad peras y “p” el costo por cada pera, que hasta el momento no conocemos; y del otro grupo, colocamos 5p por la misma razón que la explicación anterior.

 

 

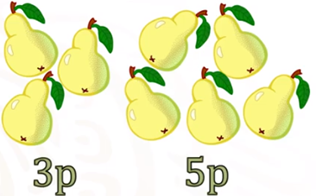
Del otro lado, tenemos una manzana donde el costo por ella lo representaremos solamente con la literal m, tenemos otras 3 manzanas, su costo lo representaremos como 3m y por último 2 manzanas cuyo costo lo representaremos con 2m.

 

 

Por medio de la adición representemos el costo total de las peras, como 3p + 5p, del otro lado representaremos, el costo por todas las manzanas, como m + 3m + 2m. Del lado de las peras, reduciendo nuestros términos semejantes es 8p y del lado de las manzanas son 6m, ¿podríamos reducirlas en un sólo término algebraico?

 

 

Cada tipo de fruta tiene distinto precio, el cual aún no conocemos, pero los representamos con “p” y “m”. No es posible reducirlos, sólo podemos indicar que se suman, para dejar claro que tenemos el costo de 8 peras más el costo de 6 manzanas.

 

 

Ahora, revisa algunos otros ejemplos con términos algebraicos. No pierdas de vista que, los términos algebraicos semejantes son aquellos que tienen las mismas literales y los mismos exponentes.

 

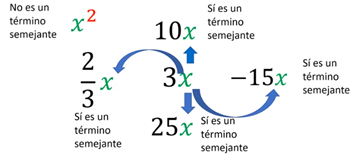
Si quieres conocer un término semejante a 3x, todos los términos que tengan esta literal y exponentes iguales, va a ser un término semejante; por ejemplo, 10x tiene la misma literal, 25x también tiene la misma literal, 15x negativo también tiene la misma literal, dos tercios de x cumple con lo misma condición, éstos son términos semejantes porque lo único que se observa son las literales y los exponentes. Un término que no sería semejante es “x” al cuadrado, aunque es la misma literal “x” tiene exponente 2, por lo tanto ya no se considera semejante.

 

 

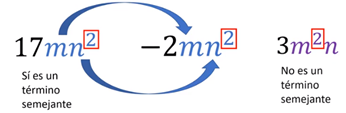
Segundo ejemplo: -2mxn2  un término semejante debe tener exactamente las mismas literales y los mismos exponentes. El término 17mn2 es un término semejante porque tiene las mismas literales y exponentes. Y 3m2n  no es un término semejante porque, aunque tiene las mismas literales, sus exponentes no son iguales.

 

 

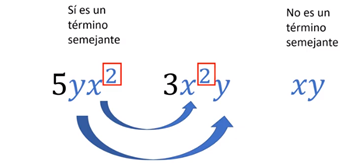
Un último ejemplo: 3x2y; el término 5yx2 podría ser semejante porque aunque las literales están en un orden distinto, siguen siendo las mismas y conservan sus exponentes; y el término xy, no es un término semejante, porque aunque son las mismas letras y en el mismo orden, no tienen los mismos exponentes.

 

 

Dado lo anterior, utilizarás los términos semejantes para encontrar la solución de ecuaciones lineales; considera que ya has hecho uso de los procedimientos para resolver distintos tipos de ecuaciones. En este caso resolverás una ecuación con paréntesis:

 

 

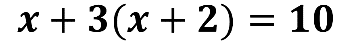
Para poder resolver esta ecuación, puedes apoyarte de una propiedad distinta a las que ya has estudiado; y ésta es la propiedad distributiva.

 

La propiedad distributiva, relaciona a la adición con la multiplicación y se enuncia así: El producto de un número por una adición es igual a la suma de los productos parciales de dicho número por cada sumando que interviene en la adición. Es decir:

 

 

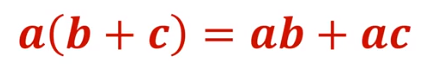
Por ejemplo: 5 que multiplica a 3 más 9, aplicando la jerarquía de operaciones primero se resuelve la adición que está dentro de los paréntesis, y esto es igual a 5 (12) y el producto es 60.

 

5(3+9) = 5(12) = 60

 

La propiedad distributiva dice que 5 que multiplica a 3 más 9 es igual a multiplicar a 5 por 3 más 5 por 9; resolviendo esto es igual a 5 por 3, 15 más 5 por 9, 45; 15 más 45 es igual a 60. Observa que se obtuvieron los mismos resultados.

 

 

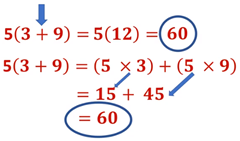
De la misma forma, el producto de un número por una sustracción, es la sustracción de los productos parciales de dicho número por el minuendo y sustraendo que intervienen en la sustracción. Es decir:

 

 

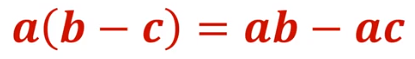
Por ejemplo: 7 que multiplica a 6 menos 2 es igual, aplicando la jerarquía de operaciones se resuelve primero la sustracción que está dentro de los paréntesis, lo que resulta 7 por 4 y el producto es 28.

 

7(6-2) = 7(4) = 28

 

La propiedad distributiva enuncia que 7 que multiplica a 6, menos 2 es igual a 7 por 6, menos 7 por 2; resolviendo es igual a 7 por 6, 42, menos, 7 por 2, 14; y esto es igual a 28; no dejes de observar que se obtienen los mismos resultados.

 

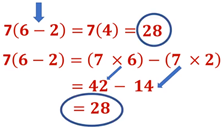
Como en una ecuación, las incógnitas representan números desconocidos, también podríamos aplicar la propiedad distributiva. Por ejemplo: 3 que multiplica a “x” más 5; primero multiplicamos 3 por “x” y es igual a 3x más 3 por 5 es igual a 15; debido a que ya no tenemos términos semejantes nuestro resultado final es igual a: 3x más 15.

 

 

Ahora que conoces la propiedad distributiva, puedes dar respuesta a la ecuación:

 

Te invitamos a que apliques lo que acabas de aprender, resolviendo la siguiente ecuación con paréntesis: x + 3 (x + 2) = 10 pero también es válido decir, 3. x+ 2 = 10

 

Como primer objetivo se elimina el paréntesis en la ecuación, para eso nos apoyaremos de la propiedad distributiva, donde multiplicaremos 3 por “x”; y posteriormente, 3 por 2, esto resulta x + 3x + 6 = 10  Observa que tenemos términos semejantes en esta ecuación, que son x + 3x, reduciendo tenemos 4x + 6 = 10  por medio de la propiedad uniforme de la igualdad restaremos en ambos miembros de la igualdad 6, tenemos:  4x + 6 - 6 =  10 – 6

 

Al restar 6 a 6 el resultado es 0, y en el segundo miembro 10 positivo menos 6 es igual a 4; obteniendo 4x = 4

 

Utilizando nuevamente la propiedad uniforme, dividiendo entre 4 ambos miembros, resulta 4x sobre 4 es = a 4 sobre 4. Sabemos que 4 entre 4 es 1, por lo que resulta x = 1

 

 

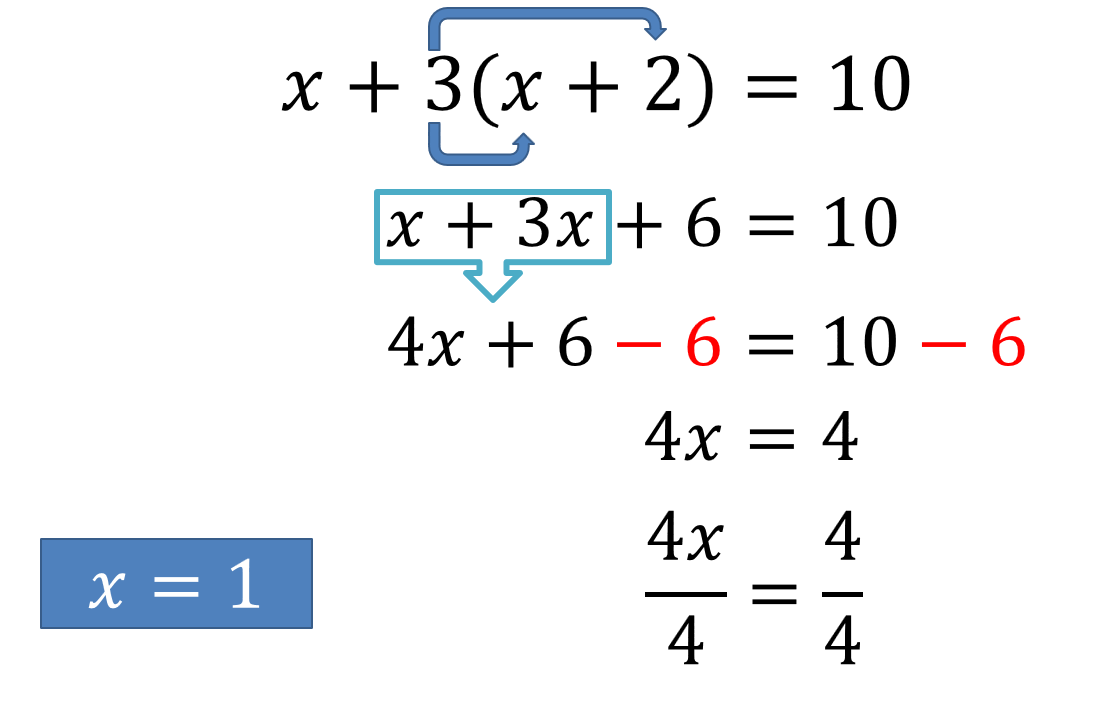
Para saber si el valor obtenido para “x” es el correcto, se realiza la comprobación, en donde se tiene que sustituir el valor encontrado para “x” en la ecuación.

 

 

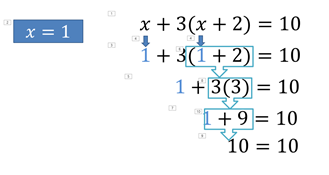
Resuelve un ejemplo más, haciendo uso de la propiedad distributiva, en la siguiente ecuación:

 

 

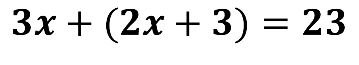
Por medio de la propiedad distributiva, demos solución a este nuevo ejemplo.

 

Como primer objetivo será eliminar los paréntesis en la misma, para eso nos apoyaremos de la propiedad distributiva, donde multiplicaremos cada término que están al interior del paréntesis por 1, esto resulta 3x + 2x + 3 = 23

 

Observen que tenemos términos semejantes en esta ecuación, que son 3x + 2x reduciendo tenemos 5x + 3 = 23  por medio de la propiedad uniforme, restamos en ambos miembros de la igualdad 3  tenemos 5x + 3 - 3 = 23 - 3, sabemos que 3 – 3 es igual a 0, y al restar 23 - 3 = 20; obteniendo 5x = 20, apoyémonos nuevamente de la propiedad uniforme y dividamos por 5 ambos miembros, resulta 5x entre 5 = 20 entre 5  sabemos que 5 entre 5 es 1  y obtenemos x = 20 sobre 5, resulta x = 4

 

 

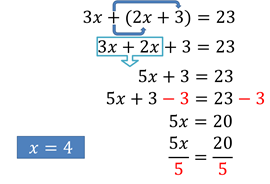
Para tener la certeza de que el resultado sea el correcto, realiza la comprobación sustituyendo el valor de X

 

 

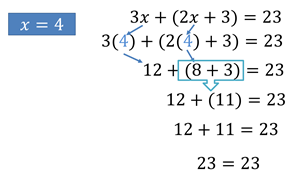
Es así, como los términos semejantes son aquellos que tienen las mismas incógnitas con los mismos exponentes, aunque los coeficientes sean diferentes. La propiedad distributiva enuncia que, el producto de un número por una adición, es la suma de los productos parciales de dicho número por cada sumando que interviene en la adición; lo mismo que en el caso de la sustracción, por lo tanto, esta propiedad nos ayuda a eliminar paréntesis y así a reducir los términos semejantes.

 

 

Reto de hoy.

 

Construye el procedimiento, conforme a lo que aprendiste en la lección, de la siguiente ecuación:

 

 

Atención en que colocamos el valor de “m” para que verifiques que lo lograste. Adicional a ello realiza la comprobación para que te asegures de que lo hiciste bien.