calificaciones parciales del trimestre 2
1° E
1°F
1°K
viernes, 26 de febrero de 2021
miércoles, 24 de febrero de 2021
clase 24 de febrero del 2021 tema: notación algebraica ejercicio 14 del libro de algebra de Baldor
clase 24 de febrero del 2021
tema: notación algebraica
ejercicio 14 del libro de algebra de Baldor
1. Escríbase la suma de a, b y m .
2. Escríbase la suma del cuadrado de in, el cubo de b y la cuarta potencia de x.
3. Siendo a un número entero, escríbanse los dos números enteros consecutivos posteriores a a .
4. Siendo x un número entero, escríbanse los dos números consecutivos anteriores a x .
5. Siendo y un número entero par, escríbanse los tres números pares consecutivos posteriores a y .
6. Pedro tenía $a, cobró $x y le regalaron $m . ¿Cuánto tiene Pedro?
7. Escríbase la diferencia entre m y n.
8. Debía x bolívares y pagué 6 . ¿Cuánto debo ahora?
9. De una jornada de x Km . ya se han recorrido m Km . ¿Cuánto falta por andar?
10. Recibo $x y después $a. Si gasto $m, ¿Cuánto me queda?
11. Tengo que recorrer m Km. El lunes ando a Km., el martes b Km. y el miércoles c Km . ¿Cuánto me falta por andar?
12. Al vender una casa en $n gano $300 . ¿Cuánto me costó la casa?
13. Si han transcurrido x días de un año, ¿cuántos días faltan por transcurrir?
14. Si un sombrero cuesta $a, Icuánto importarán 8 sombreros ; 15 sombreros; m sombreros?
15. Escríbase la suma del duplo de a con el triplo de b y la mitad de c .
16. Expresar la superficie de una sala rectangular que mide a m . de largo y b m. de ancho.
17. Una extensión rectangular de 23 m . de largo mide n m. de ancho. Expresar su superficie.
18. ¿Cuál será la superficie de un cuadrado de x m . de lado?
19. Si un sombrero cuesta $a y un traje $b, ¿cuánto importarán 3 sombreros y 6 trajes?, ¿x sombreros y m trajes?
20 . Escríbase el producto de a + b por x + y.
21. Vendo (x + 6) trajes a $8 cada uno. ¿Cuánto importa la venta?
22 . Compro (a - 8) caballos a (x + 4) bolívares cada uno . ¿Cuánto importa la compra?
23. Si x lápices cuestan 75 sucres ; ¿cuánto cuesta un lápiz?
24. Si por $a compro m kilos de azúcar, ¿cuánto importa un kilo?
25. Se compran (n - 1) caballos por 3000 colones. ¿Cuánto importa cada caballo?
26 Compré a sombreros por x soles . ¿A cómo habría salido cada sombrero si hubiera comprado 3 menos por el mismo precio?
27. La superficie de un campo rectangular es m m .2 y el largo mide 14 m . Expresar el ancho .
28. Si un tren ha recorrido x + 1 Km . en a horas, ¿cuál es su velocidad por hora?
29. Tenía $a y cobré $b. Si el dinero que tengo lo empleo todo en comprar (m - 2) libros, ¿a cómo sale cada libro?
30 En el piso bajo de un hotel hay x habitaciones . En el segundo piso hay doble número de habitaciones que en el primero ; en el tercero la mitad de las que hay en el primero . ¿Cuántas habitaciones tiene el hotel?
31 . Pedro tiene a sucres ; Juan tiene la tercera parte de lo de Pedro ; Enrique la cuarta parte del duplo de lo de Pedro . La suma de lo que tienen los tres es menor que 1000 sucres . ¿Cuánto falta a esta suma para ser igual a 1000 sucres?
viernes, 19 de febrero de 2021
PLANILANDIA (LIBRO DE CUENTO)
PLANILANDIA
PELICULA COMPLETA
El primer capítulo de Planilandia es una descripción general por parte de nuestro personaje principal, el cuadrado, de su mundo. Da por sentado que existen otros mundos: Espaciolandia. Este mundo es muy importante debido a la revelación que nos hará un personaje conocido, aunque eso será posteriormente.
El siguiente capítulo habla especialmente del clima en Planilandia y como ellos calculan el norte: es debido a su atracción natural hacia al sur, ya que ellos no conocen el concepto de “arriba”. También al referirse a las casas en Planilandia, habla por primera vez de las mujeres, de cómo deben ellas entrar por una puerta diferente a la de los hombres, todo esto debido a la segregación que existe en su mundo.
En el capítulo tres explica las diferencias sociales entre las diversas castas de Planilandia. Como él explica, las líneas son los estratos más bajos, representando a las mujeres. La siguiente clase son los triángulos isósceles, que al tener menos algunos son menos racionales. Esta clase está reservada exclusivamente a los soldados u obreros, y los que no cumplen esta función son propensos a convertirse en criminales, que son condenados a muerte. La clase que sigue son los cuadrados, pentágonos y triángulos equiláteros. Al tener más tienen derecho a ejercer profesiones y son pertenecientes a la clase media. Las figuras de más de seis lados son consideradas parte de la nobleza, y la clase de élite (los círculos) son figuras que tienen tantos lados que parecen círculos. Los antes mencionados son los sumos sacerdotes. Ellos rigen la vida en Planilandia.
El siguiente apartado está destinado a las mujeres. Habla de cómo las mujeres (las líneas) son la clase más baja debido a su naturaleza emocional y poco racional. Los hijos son separados de la madre después de recibir la suficiente dotación emocional, pasan a vivir con el padre para ser educado en la racionalidad. Además las mujeres son seres muy peligrosos ya que son puntiagudos, además de ser peligrosos.
El narrador nos habla de los métodos que utilizan los planilandeses para identificarse mutuamente. La vista, el tacto y la voz son las maneras en la cual ellos logran identificarse, ya que como el narrador dice, ellos no pueden percibir colores o formas onduladas, lo hacen de esta manera. Lo que hace mucho énfasis es que la identificación táctil es muy tediosa y peligrosa con una mujer.
En la parte de la identificación visual nos pone en evidencia porque es importante tener muchos ángulos. Mientras más ángulos es más fácil tener una visión más periférica.
En el capítulo número siete, nos hará referencia a las figuras irregulares. Estas son pues, todas las figuras que no tienen lados iguales. Estas son marginadas pues en la sociedad planilandesa se aprecia la regularidad. Estas pueden tomar terapia para ser regulares y así ser aceptadas dentro de su sociedad.
Antiguamente las clases sociales se identificaban con colores, pero esta práctica fue prohibida hasta el punto que solo existía un color universal y que al final desembocara en un conflicto.
Después de una guerra en la cual los rebeldes isósceles combatían por lograr distribuir equitativamente la práctica de los sujetos de pintarse los lados (aspirando a que incluso los sacerdotes siguieran dicha norma), Pantociclo, el jefe de las clases reaccionarias se erigió como vencedor. En un engaño, haciéndole creer a los isóceles de su capitulación a favor de las propuestas de los primeros, Pantociclo realiza una emboscada dentro de un edificio parlamentario, ordenándole a sus huestes acribillar hasta al último rebelde. A partir de entonces, el uso del color como otro método de identificación entre los planilandeses, quedó prohibido, así como su producción regulada por el Estado.
Posteriormente, el cuadrado se ocupa de describirle al lector lo que es la clase sacerdotal de Planilandia. Afirma que si bien son conocidos como círculos, los sacerdotes en realidad son polígonos de tal cantidad de lados que resulta imposible distinguirlos de un círculo propiamente dicho .Señala que, a diferencia de nuestra concepción de un sacerdote como alguien responsable únicamente de actividades religiosas, los sacerdotes planilandeses se ocupan de dirigir una variedad de actividades sociales en el país de las dos dimensiones: la teología, el arte, las ciencias y el gobierno, entre otras. Igualmente, advierte que cualquier planilandés de posición social baja debe abstenerse de tocar a los círculos ya que, siendo objetos de veneración tan profunda en la sociedad planilandesa, se cometería un sacrilegio.
A continuación, el cuadrado realiza una descripción de la doctrina que pregonan los sacerdotes. Entre ellos existe la noción de una especie de determinismo geométrico, en la que se cree que las características geométricas de los individuos forjan sus respectivas personalidades. Evidentemente, si un habitante de Planilandia es perfectamente regular, significa que será un sujeto de buen actuar y pensar; por el contrario, si padece de alguna irregularidad, el infortunado ser estará poco menos que condenado a llevar una vida de crimen, idiotez y poca solvencia moral. Es por ello que las clases medias planilandesas han recurrido a métodos de modificación geométrica, enviando a sus hijos a terapias médicas que tienen como fin aumentar su número de lados.
Entrando al segundo apartado de la novela, “Otros mundos”, el cuadrado comenzará su viaje al descubrimiento de otras realidades. En la víspera de año nuevo (a punto de comenzar el año 2000), el cuadrado sueña con un mundo de una sola dimensión, con forma de línea recta, en la que una recta larga al medio, otras líneas rectas más cortas y brillantes puntos se movían en la misma dirección y hacían ruidos extraños. Sorprendido, el cuadrado se aproxima a dicha región y entabla un diálogo con la línea más larga del lugar, que resulta ser el rey de Linealandia. Debido al asombro, el cuadrado realiza una serie de preguntas al monarca sobre la naturaleza de su reinado, por ejemplo: ¿cómo se consuma el matrimonio entre las líneas (los hombres) y los puntos (las mujeres)? Por medio del sonido, contesta el Rey. Los habitantes de Linealandia, al encontrarse todos en una misma recta y al no poder atravesar físicamente a sus compatriotas contiguos, han desarrollado la habilidad de emparejarse de manera polígama (2 mujeres por cada hombre) por medio de la entonación de sonidos para la conformación de armonías vocales.
Posteriormente, el cuadrado emprende la misión de explicarle al rey de Linealandia que su realidad, si bien existente, no es más que un segmento de una experiencia más amplia. Los linealandeses únicamente pueden moverse en dos direcciones: norte y sur (que conforman la primera dimensión). Sin embargo, el cuadrado quiere hacerle ver al monarca que existen otras (por el momento) dos únicas dimensiones más que dan forma a la segunda dimensión: la izquierda y la derecha. El Rey evidentemente responde incrédulamente, señalando los disparates que cree el cuadrado le está diciendo. Posteriormente, el monarca le pide a su interlocutor que demuestre empíricamente su tesis. El cuadrado fácilmente sale de la dimensión “norte-sur”, dejando de ser visible para el Rey pero sin dejar de ser audible para el mismo; el monarca simplemente concluye que el extranjero domina un arte de desaparición. El cuadrado, frustrado por la poca flexibilidad intelectual del soberano linealandés, decide abandonar su cometido.
Habiendo despertado de su sueño, el cuadro se dirige al comedor con el resto de su familia. Un pequeño hexágono, nieto del cuadrado y a quien da clases de geometría, señala que si se puede calcular la superficie del interior de las personas, es decir, el área (lado al cuadrado); se pregunta por el significado de “lado a la tercera potencia”, que hace referencia al volumen de un cuerpo geométrico. Su maestro y abuelo cuadrado le indica que esto no tiene significado en la geometría planilandesa, al existir únicamente dos dimensiones. Cansando por la insistencia de su descendiente sobre la cuestión, el abuelo decide terminar la lección del día. Sin poder abandonar el pensamiento sobre el asunto, el cuadrado le expresa lo que cree que es una tontería del menor. Sintiendo una presencia extraña en la habitación, el cuadrado y su esposa se encuentran con el impactante de hecho de encontrarse frente a un peculiar círculo (en apariencia, ya que en realidad se trata de una esfera) que les afirma que el muchacho en realidad acertó en su juicio. Es en este momento en el que la esfera comienza el Evangelio de la Tercera dimensión.
En el capítulo 16 el cuadrado hace la identificación de la esfera mediante el tacto, al tocarlo se da cuenta que es un círculo y se disculpa con ella, el cuadrado le pregunta que de donde proviene y la esfera le comenta que de Espaciolandia, y empieza una discusión sobre que es realmente Espaciolandia. La esfera le comenta que cuando descendió de Espaciolandia pudo observar la casa del cuadrado y le describe todo lo que hay en su casa desde una perspectiva aérea. Posteriormente la esfera le empieza a explicar la existencia de una tercera dimensión la cual los habitantes de Espaciolandia no pueden percibir, el cuadrado no puede creer estas afirmaciones, y la esfera le da una serie de explicaciones pero que son en vano, trata desde la aritmética explicarle la altura de los objetos. En el siguiente capítulo 17 el cuadrado ataca a la esfera pero se da cuenta que no la puede lastimar, después la esfera trata de demostrarle con hechos la existencia de una tercera dimensión, le roba un cuaderno de su armario y el después se lo enseña, el cuadrado cree que se trata de un mago o algo por el estilo. La esfera irritada le dice al cuadrado que va a tener que usar el último método y se lo lleva a Planilandia.
En el capítulo 18 al llegar a Espacio el cuadrado le comenta a la Esfera que por qué no pueden ver sus intestinos entre los habitantes de Espaciolandia, la esfera responde por que son seres compuestos, diferentes a los de Planilandia. Después la esfera lleva al cuadrado y le enseña como se ve Planilandia desde arriba, el cuadrado puede observar a sus hijos y a su esposa que está preocupada por la desaparición de él, la Esfera le propone al cuadrado hacer una inspección de Planilandia. Desde la perspectiva aérea el cuadrado puede ver a toda su ciudad y a sus habitantes, así como también las casas de sus vecinos. El cuadrado le comenta a la esfera que se ha convertido en Dios ya que es omnividente y la esfera le dice que en Espaciolandia todos sus habitantes tienen esta cualidad, hasta los ladrones. El cuadrado y la Esfera descienden al cónclave en donde están reunidos todas las esferas de Planilandia, y descienden en medio de la reunión, estaba presente el hermano del cuadrado que posteriormente fue encarcelado ya que al que sepa la existencia de una tercera dimensión le aguardaba la cárcel o la muerte. La esfera en medio de todo el clérigo circular se puso a proclamar la existencia de una tercera dimensión, después de esto se retiraron.
En el capítulo 19 el cuadrado nos comenta como pudo aprender más de Espaciolandia y la Esfera le enseño sobre los cilindros, cuadrados etc. Al final del capítulo la esfera y el cuadro tienen una plática de una posible cuarta dimensión y la que esta podría ser la del pensamiento. Ya para el capítulo 20 la esfera lo lleva a Puntolandia donde conoce al punto y su mundo y de la existencia de otras dimensiones. Para el capítulo 21 el cuadrado intenta explicar la teoría de la tercera dimensión acordándose de “hacia al norte pero no arriba” pero no tiene éxito al explicárselo a su nieto, pero no adquiere éxito sobre una teoría la cual no tiene como explicar la existencia de una tercera dimensión. En el último capítulo el cuadrado comenta como hace escritos y tiene pensamientos sobre cómo explicar su teoría pero no tiene éxito, lleva su propuesta al cónclave y todos los círculos eruditos lo escuchan pero no tiene éxito y termina encarcelado por sus ideas y desafiar los dogmas de Planilandia. El cuadrado nos comenta que toda esta historia nos la cuenta desde la cárcel y mientras no hable puede seguir vivo, el cuadrado escribe desde las rejas y comenta que parece una historia irreal la existencia de tres dimensiones así como también la misma Planilandia.
“Las emociones en la educación"
“Las emociones en la educación"
"En la ciencia de la neurobiología, autores como Antonio Damasio, Humberto Maturana y Francisco Varela se han dedicado al estudio del sistema neurológico y han establecido que los aprendizajes dependen de las emociones. Apoyados en este dato, psiquiatras como Pekrum, Boegarts, Leduc, Hadjy han estudiado cómo ciertas emociones abren las posibilidades de aprendizaje, mientras que otras las cierran. Si miramos a los obstáculos, hay muchas emociones que inhiben y son amenazas para que pueda ocurrir el aprendizaje en los niños. Por ejemplo, el miedo produce una concentración de la atención, pero por solo unos instantes, muy rápidamente produce vacíos en la atención, produciendo así distracción. (Como dato, en promedio, los niños están distraídos alrededor del 80% del tiempo en que están en clase). El sentirse amenazado, da lugar a un efecto de “giro involutivo” que produce desamparo, haciendo que los niños no se sientan seguros para abrirse a las posibilidades de aprender, de superar sus esquemas mentales anteriores, los lleva a no enfrentar los desafíos que implica el aprendizaje, los deja con el sentimiento que no pueden acceder a sus propias capacidades. La neurociencia ha descubierto que la educación tradicional (la amenazante) es compatible con la memorización, pero incompatible con el aprendizaje que requiere relacionar, crear y desarrollar pensamientos de orden superior. Pero este campo no es un espacio determinista, como podría sugerirse de algunas prácticas de origen conductista. Ella varía según las personas. Por ejemplo, lo que más se ha estudiado es el efecto de la ansiedad, sin embargo, sus efectos son ambiguos, pues a veces inhiben y otras veces estimulan el desempeño de los niños, eso depende de cada niño o niña. Investigaciones recientes apuntan a las emociones son un factor importante y estable en la predicción del desempeño de los alumnos. Emociones tales como la vergüenza que sienten los alumnos, la rabia, el aburrimiento, la pena o la desesperanza no son favorables al aprendizaje porque minan el esfuerzo, producen pensamiento irrelevante y distraen. Por otra parte, las emociones favorables como la apertura, el entusiasmo, el gusto por aprender, el orgullo, la esperanza de aprender, son todas emociones favorables al aprendizaje. Pekrum ha demostrado que las emociones en el campo académico predicen el esfuerzo que los alumnos harán en sus estudios, la determinación de estrategias flexibles de aprendizaje, la manutención y desarrollo de recursos de atención disponibles para el aprendizaje y que culminan en el desempeño académico”
lunes, 15 de febrero de 2021
primeros años Volumen de prismas rectos 24/11/2020
Volumen de prismas rectos
Aprendizaje esperado: Calcula el volumen de prismas rectos, cuya base sea un triángulo o un cuadrilátero, desarrollando y aplicando fórmulas.
Énfasis: Calcular el volumen y las medidas de prismas rectos.
¿Qué vamos a aprender?
Calcularás el volumen de prismas cuya base sea un triángulo o un cuadrilátero. Además, analizarás las fórmulas, las cuales te permiten obtener cualquier medida de los prismas.
¿Qué hacemos?
La geometría es una de las ramas de las matemáticas que ha inspirado a muchas personas a lo largo de la historia, para realizar numerosas creaciones. Por ejemplo, arquitectos y artistas se han basado en figuras geométricas para crear esculturas, construir edificios, monumentos y muchas cosas más de distintos tamaños, formas y colores.
En todo el mundo se pueden apreciar estas creaciones y en México también, por lo que es muy probable que identifiques objetos o edificaciones a tu alrededor con formas geométricas. Por otro lado, además del lado estético, está el lado funcional, ya que hay edificios que alojan a una gran cantidad de personas debido a sus dimensiones y al volumen que pueden contener.
Por ejemplo, en el corazón de la Ciudad de México, se encuentra la Torre Latinoamericana, que tiene una altura de más de 180 metros, con 44 niveles y en la que caben, aproximadamente, 10 mil personas. Esta Torre, tiene la forma de un prisma, cuyas caras laterales son cuadriláteros y su base tiene forma cuadrangular. Está inspirada en el edificio Empire State de la ciudad de Nueva York y es uno de los rascacielos latinoamericanos más altos.
https://www.instagram.com/p/BzySS4HjjiC/?igshid=vxwfgklwhvy5
Este tipo de edificaciones puede albergar a muchas personas debido al volumen que tiene, por lo que se convierten en importantes puntos de trabajo y turismo de las comunidades en las que se construyen.
En la Ciudad de México hay otro rascacielos más alto que la Torre Latinoamericana, cuya base no es cuadrangular sino rectangular, se trata del World Trade Center de la Ciudad de México. Ambos rascacielos tienen la forma de prismas, aunque la forma de sus bases es diferente.
En esta ocasión, vas a aprender cómo calcular el volumen de distintos tipos de prismas. Los prismas son formas muy comunes a tu alrededor, por lo que conocer cómo calcular el volumen de estas figuras puede ser de utilidad, para que conozcas más sobre el tema revisa el siguiente audiovisual.
- 29. El volumen de prismas rectangulares.
Revisa del minuto 00:56 al 01:06 y del 01:25 al 02:48.
Como pudiste observar, las unidades de medida del volumen son unidades cúbicas. En el video, se calculó el volumen de un prisma cuya base es rectangular y se hizo con pequeños cubos de madera que representaron las unidades cúbicas.
El cálculo se desarrolló analizando la construcción del prisma, es decir, agregando niveles al cuerpo geométrico. Se comenzó con el primer nivel, que representa la base del prisma y se fueron agregando niveles, que representan la altura del prisma.
Como viste, es posible agregar niveles a la base del prisma, lo que hace que la altura aumente y, en consecuencia, su volumen. Pero, ¿Qué pasaría con el volumen si a la figura de 12 cubos de base, del ejemplo, le agregarás dos niveles más? ¿Sería posible obtener una fórmula general para calcular el volumen de cualquier prisma? Para dar respuesta a estas preguntas, revisa el siguiente video.
- 29. El volumen de prismas rectangulares.
Revisa del minuto 03:05 al 03:41 y del 04:42 al 05:30
A partir de lo que viste, se puede decir que, el volumen de un prisma recto se calcula con la fórmula: Volumen = Área de la base por la altura.
Existen diferentes prismas rectos, dependiendo de la forma de su base. Por ejemplo, en el Estado de México, el arquitecto Luis Barragán se inspiró en prismas triangulares para construir unas torres con esa forma, conocidas como las Torres de Satélite y están ubicadas en el municipio de Naucalpan de Juárez. Son prismas rectos con base triangular, que con diferentes colores dan una apariencia cosmopolita a una de las vialidades más importantes del estado.
https://www.instagram.com/p/B8fxv82pFRq/?igshid=1dwk74w3v7iuo
Ya sabes cómo se calcula el volumen de un prisma rectangular, ahora, analiza cómo, a partir de ese conocimiento, se puede obtener la fórmula para la medida del volumen de un prisma triangular. Observa con atención el siguiente video:
- 62. Volumen de prismas triangulares.
Revisa del minuto 00:51 al 03:32
Como pudiste observar, en el caso de los prismas triangulares, también se cumple la fórmula general que se obtuvo antes, es decir: Volumen es igual a área de la base por la altura.
En este caso el área de la base corresponde al área de un triángulo. Recuerda que el área de un triángulo, se calcula multiplicando la base por la altura y luego dividiendo entre dos, es decir base por altura sobre dos.
Ahora, calcula el volumen de un prisma triangular cuya altura es de 10 cm y que tiene como base un triángulo rectángulo. Las medidas de dicho triángulo son: 5 cm en su lado que corresponde a su base y 4 cm en su lado que coincide con su altura.
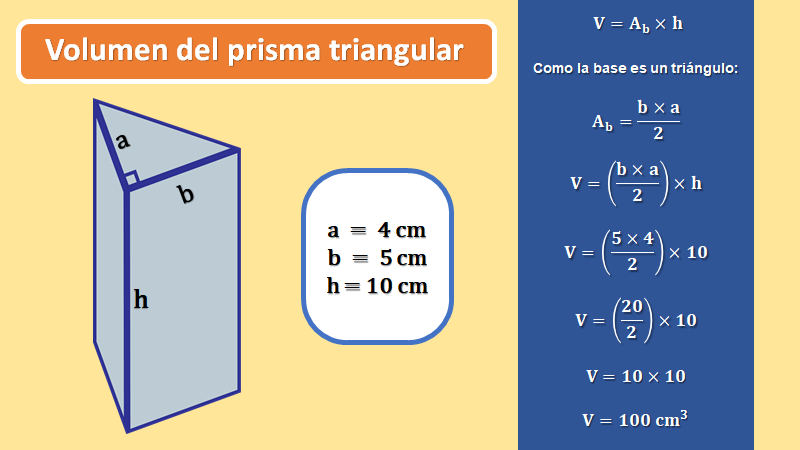
Para ello, se utiliza la fórmula, volumen igual a área de la base por altura. Si sabes que la base es un triángulo y la fórmula para calcular su área es: base por altura sobre dos, debes cambiar el área de la base por: base por altura sobre dos.
Sustituyes los datos en la fórmula, quedando: volumen es igual a 5 por 4 sobre 2 cuyo resultado se multiplica 10.
Realizas las operaciones, que son:
5 por 4, igual a 20.
20 entre dos, igual a 10.
Finalmente, 10 por 10 igual a 100.
Esto quiere decir que el volumen es igual a 100 cm cúbicos.
Parece que puedes calcular el volumen de un prisma recto, si sabes calcular el área de la base.
Escribe en tu cuaderno cuál será la fórmula para calcular el volumen de un prisma con base trapezoidal y romboidal.
Probablemente, tú ya conoces las fórmulas para calcular el volumen de esos prismas si las asocias con las fórmulas para calcular el volumen de prismas cuya base sea un cuadrilátero. ¡Presta atención! para verificar tus respuestas, después de que veas el siguiente video.
- 63. Volumen de prismas cuadrangulares.
Revisa del minuto00:37 al 05:06
Pudiste ver en el video, que para calcular el volumen de un prisma recto con base triangular, o bien, con la forma de un cuadrilátero, requiere que conozcas el área de su base. Una vez que la conoces sólo tienes que multiplicar por la altura del prisma para conocer su volumen.
Como puedes observar hay más objetos, además de edificaciones, que tienen forma de prismas rectos. Por ejemplo, ahora revisarás como calcular el volumen de un tope con forma de prisma trapezoidal que viste en el audiovisual. Para ello usarás la fórmula: volumen es igual al área de la base por la altura.
La base del prisma es un trapecio y si recuerdas, que la fórmula del área de un trapecio es igual a la suma de la Base mayor más la base menor, por su altura entre 2, puedes calcular el área de la base del tope. Solamente necesitas sustituir en la fórmula del volumen el área de la base por la fórmula del área de un trapecio, quedando: volumen es igual a Base mayor más base menor entre dos por la altura del trapecio, cuyo resultado se multiplica por la altura del prisma.
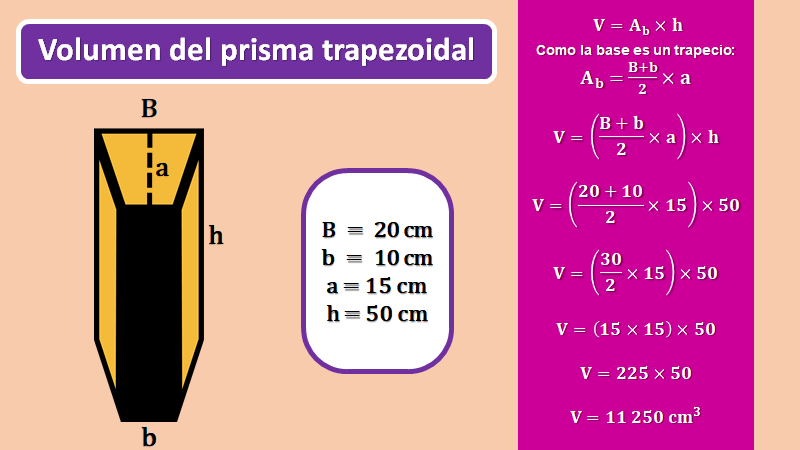
Sustituyendo los valores queda: volumen es igual a 20 más 10 sobre dos por 15, cuyo resultado se multiplica por 50.
Realiza las operaciones:
20 más 10 resulta 30.
30 sobre 2 resulta 15.
15 multiplicado por 15 resulta 225.
Finalmente, 225 por 50 resulta 11,250.
Así que el volumen es igual a 11,250 centímetros cúbicos.
Revisa otro ejemplo, en donde se calcula el volumen de la siguiente figura que es un prisma recto cuya base tiene la forma de un rombo.
La fórmula para calcular el área de un rombo es igual a diagonal mayor por diagonal menor entre 2.
Las medidas de las diagonales son: la diagonal mayor mide 20 cm de longitud y la diagonal menor mide 15 cm de longitud.
Por otro lado, es necesario conocer el volumen y para ello, se debe saber la longitud de la altura, que en este caso es de 30 cm.
Ahora, observa la fórmula para calcular el volumen del prisma. Toma nota y ve resolviendo las operaciones para calcular el volumen del prisma romboidal.
La fórmula es: A = D x d/2 es decir el área de un rombo es: Diagonal mayor por diagonal menor entre 2.
Después escribe las operaciones que son:
20 cm x 15 cm ÷ 2 = 300 cm2 ÷ 2 = 150 cm2
Sustituye los valores de la base del prisma:
El valor de la longitud de la diagonal mayor es de 20 cm que multiplicará al valor de la longitud de la diagonal menor que es 15 cm, lo que resulta 300 cm cuadrados. Después, divides el resultado entre dos, así que, el valor del área de la base del prisma es 150 cm cuadrados.
Por otro lado, como ya viste, la fórmula general para calcular el volumen de un prisma recto es: V = Abx h, es decir volumen es igual al área de la base por la altura.
Se sustituyen los valores, en donde el área de la base es de 150 cm cuadrados, que multiplica a la altura que tiene una longitud de 30 cm, lo que resulta 4,500 cm cúbicos.
150 cm2x 30 cm = 4 500 cm3
Como has visto, es posible conocer el volumen de cualquier prisma recto, si aplicas la fórmula que revisaste, es decir, si calculas el área de su base y la multiplicas por la altura.
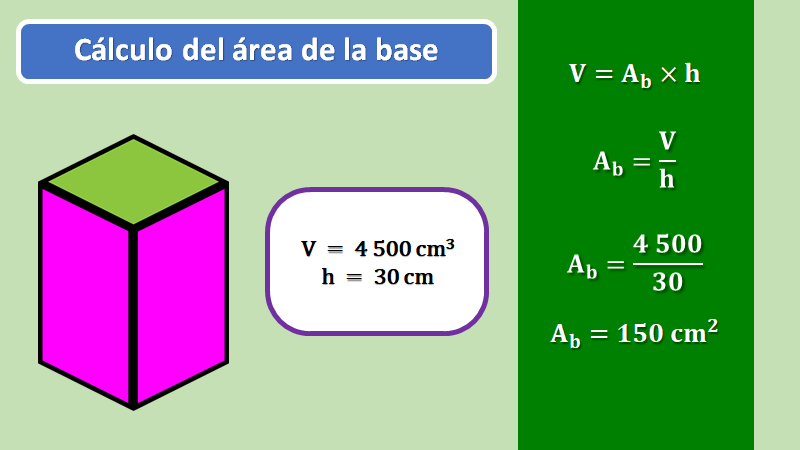
Para ello, es necesario conocer y tener presentes las fórmulas para calcular el área del triángulo y de los cuadriláteros. A partir de la fórmula general del volumen de un prisma recto, también es posible calcular cualquier medida del prisma si se conocen, al menos, dos medidas. Es decir, si conoces la altura y el volumen, puedes calcular el área de la base.
Por ejemplo, en la fórmula general para el volumen de un prisma recto, despejas el área de la base, es decir, aplicas las propiedades de la igualdad y, como has visto, al resolver ecuaciones lineales, en ese caso la fórmula sería: Área de la base, es igual a volumen del prisma entre su altura.
Para el caso del prisma, que se revisó, conoces que el volumen es de 4,500 cm cúbicos y que su altura mide 30 cm, entonces, para conocer la medida de la base, divides 4,500 centímetros cúbicos entre 30 cm y obtienes el área de la base, que es de 150 cm cuadrados.
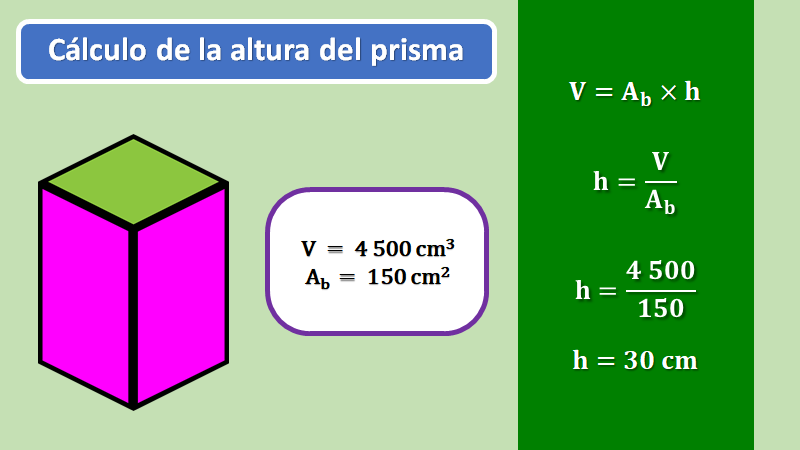
De la misma forma podrías obtener una fórmula para calcular la altura, cuando se conoce el volumen y el área de la base.
En este caso se despeja la altura. Nuevamente aplicas las propiedades de la igualdad. Así tienes que: Altura es igual a volumen entre el área de la base.
Retoma nuevamente el caso del prisma, en donde conoces que el volumen es de 4,500 cm cúbicos y que el área de la base mide 150 cm cuadrados, si divides, 4,500 cm cúbicos entre 150 cm cuadrados, obtienes la altura que es de 30 cm.
De esta forma puedes obtener cualquier medida de un prisma recto si conoces 2 de las 3 medidas involucradas en la fórmula general del volumen.
Puedes elaborar un formulario de áreas y volúmenes para organizar toda la información que has aprendido hoy. Si es posible, muéstraselo a tu maestra o maestro para recibir retroalimentación.
De igual forma si tienes alguna duda puedes solicitar la retroalimentación de tu maestra o maestro a distancia. También puedes consultar tu libro de texto en formato digital en la página oficial de la Secretaría de Educación Pública.
Has concluido el tema del día de hoy.
El reto que se propone para esta sesión es construir un prisma recto con la base que más te agrade, puede ser un cuadrilátero o un triángulo. Puedes hacerlo con cartón, plastilina o cualquier otro material moldeable; o bien, lo puedes dibujar en tu cuaderno. Decora tu prisma a tu gusto y haz uso de material reciclado que tengas a la mano.
Ya que lo hayas realizado, calcularás su volumen.
Suscribirse a:
Entradas (Atom)
👽BIENVENIDO AL NUEVO CICLO ESCOLAR 2024 -- 2025
-
TERCEROS FECHA: 09/10/2020 Homotecia Aprendizaje esperado: Explica el tipo de transformación (reflexión, rotación o traslación) que se ap... -
JUEGO PIENSA UN NÚMERO: LA MAGIA DEL ÁLGEBRA Las actividades del tipo “Piensa un número” son actividades que apoyan con fuerza el proces... -
terceros años 23/10/2020 Binomios conjugados Aprendizaje esperado: Resuelve problemas que implican el uso de ecuaciones de segundo grado. ...