PRIMER GRADO FECHA: 01/10/2020 Fraccionando las cosas

 

PRIMER GRADO

FECHA: 01/10/2020

Fraccionando las cosas

Aprendizaje esperado: Convierte fracciones decimales a notación decimal y viceversa. Aproxima algunas fracciones no decimales usando la notación decimal. Ordena fracciones y números decimales.

 

Énfasis: Ubicar fracciones en la recta numérica, comparar fracciones y estudiar la propiedad de densidad de los racionales.

 

 

¿Qué vamos a aprender?

 

En algunos casos, utilizamos la recta numérica o segmentos de ella para ubicar fracciones y poder compararlas visiblemente. Un ejemplo claro de lo anterior son las disciplinas deportivas, en particular el salto triple de longitud; el cual podemos ver cada 4 años en los Juegos Olímpicos. Cuando presenciamos esa disciplina no podemos ver de forma precisa los resultados de cada atleta, pero sabemos cuándo uno supera al otro al mirar la marca que dejan en la arena; y es hasta el momento en que se realizan las mediciones que podemos conocer las fracciones de metro que aventajan a un competidor de otro. Por ejemplo, en el salto observamos cuando un atleta salta dos tercios en la arena y cuando otro llega a la mitad de la arena; entonces consideramos que el primero superó al segundo.

 

¿Qué hacemos?

Ubicar fracciones en la recta numérica nos facilita ver su posición y relacionarlas con algunas magnitudes. Otro ejemplo, en donde observamos la aplicación de lo anterior son los circuitos en las carreras, donde podemos ver parte de los recorridos hechos. Pero ¿cómo ubicar en la recta numérica, las fracciones? Para saberlo, observa el siguiente video:

 

Cómo ubicamos fracciones en la recta numérica

https://www.youtube.com/watch?v=xoL3W33JEvk&feature=youtu.be

Para ubicar fracciones en una recta numérica se divide la unidad de acuerdo con las partes que nos indica el denominador de la fracción que se requiere ubicar.

Veremos dos casos. Empecemos con el primero. Ubicaremos fracciones propias, que son aquellas donde el numerador es menor que el denominador; y se ubican entre el 0 y 1.

 

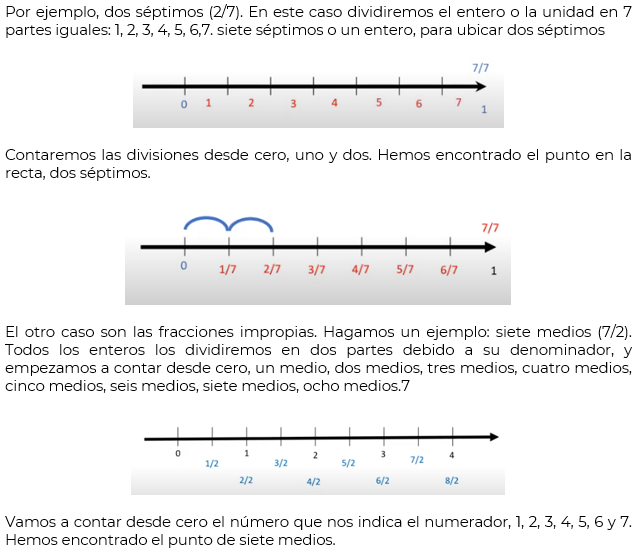
Observa otro ejemplo en el siguiente video:

3 entre 7 sobre la recta numérica

https://www.youtube.com/watch?v=orXLqgIYJb4

Observa otro ejemplo:

42 entre 5 sobre la recta numérica

https://www.youtube.com/watch?v=Ue76OuQesHU

Primero debemos dividir cada unidad en 5, ahora solo basta contar 42 porciones desde el 0 hasta llegar al 42.

¿Qué pasaría si queremos saber qué atleta corrió más que otro en alguna carrera? Tendríamos que hacer una comparación entre los datos representados como fracciones, para saber cómo comparar fracciones, observa el siguiente video:

 

Mayor que y menor que

https://www.youtube.com/watch?v=dFCTRfZtU9c

 

La fracción es un número, y sus componentes son el numerador y el denominador. Ahora compararemos fracciones que tienen el mismo denominador o el mismo numerador y compararemos cuál tiene mayor orden de magnitud, con respecto a la misma unidad de referencia.

Vamos a empezar con la primera pareja, donde tenemos cuatro séptimos (4/7) y tres séptimos (3/7), es decir, cada barra está fraccionada en 7 partes iguales de acuerdo con el denominador, lo que nos ayudará será resaltar 4 de ellas en la primera y 3 en la segunda.

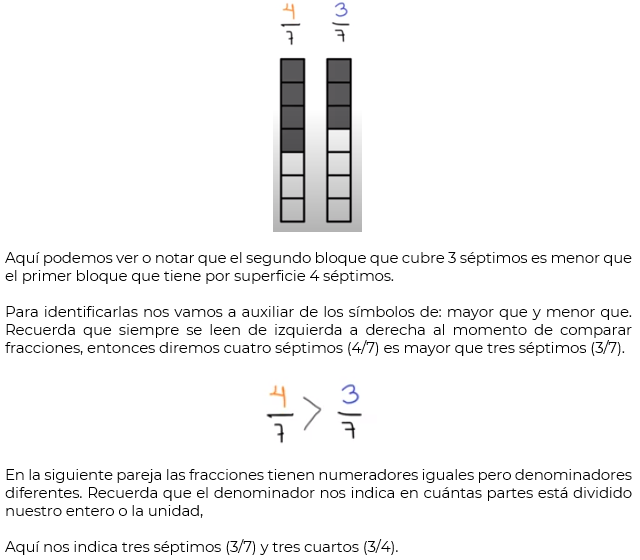
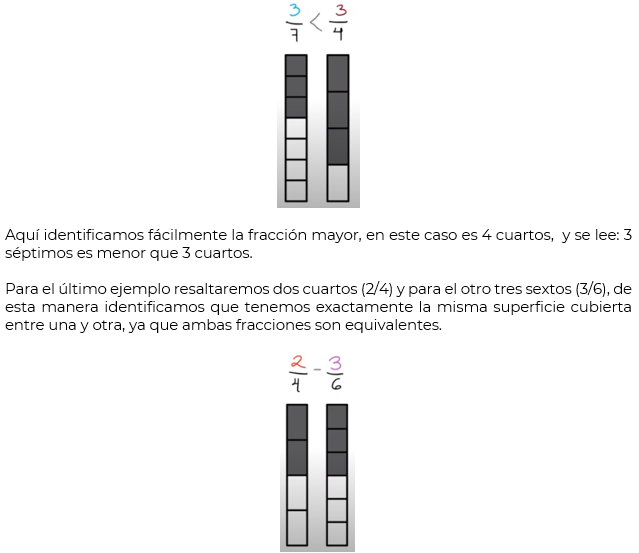
Para continuar, observa el siguiente video:

COMPARACION DE FRACCIONES

https://www.youtube.com/watch?v=tv4Uq6mPLOo&feature=youtu.be

Tenemos tres décimos y tres veinticincoavos, queremos saber ¿cuál de las dos fracciones es la de mayor orden de magnitud? Apoyémonos de las representaciones gráficas. Observa las superficies coloreadas en cada caso.

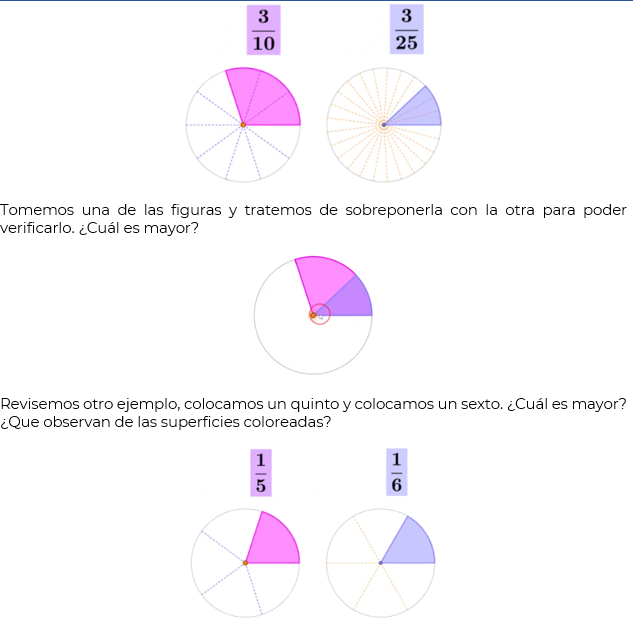
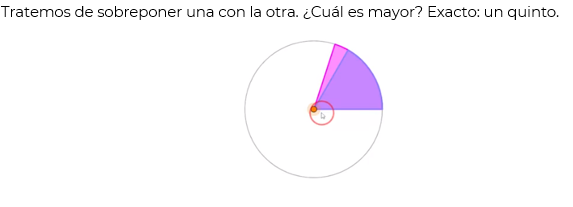
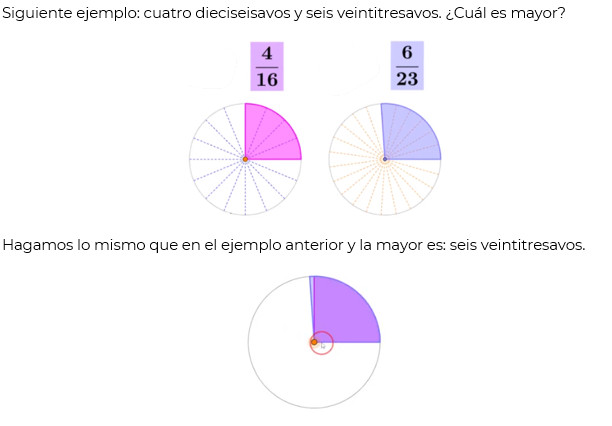
Sigamos con el tema de las competencias entre atletas, y pensemos que, si un famoso atleta mejoró su récord en la carrera de los cien metros planos, por 9.6 segundos, y que vuelve a correr y ahora hace 9.5 segundos. Sigue practicando y disminuye su tiempo entre 9.5 y 9.6 segundos ¿Eso es posible? Sí, porque hay números decimales entre estas cifras. ¿Pero existen fracciones entre un medio y tres cuartos?

 

Claro que sí y esto es debido a la propiedad de densidad de los números fraccionarios y decimales. Para entender un poco mejor observa el siguiente video del minuto 0:25 al 4:53.

 

Propiedad de densidad Fracciones y decimales 2

https://www.youtube.com/watch?v=NcwBfSL9Zoc

 

Siempre habrá un número infinito de números racionales entre cualquier pareja de números diferentes entre sí.

Ahora, observemos la densidad entre fracciones:

 

DENSIDAD DE RACIONALES

https://www.youtube.com/watch?v=TlDieVL6oUo&feature=youtu.be

 

¿Por qué los números racionales tienen la propiedad de densidad?

Para comprobarlo, nos apoyaremos de un segmento de recta numérica, vamos a elegir dos números, para este ejemplo utilizaremos el cero y el uno.

¿Cuál es el número que se encuentra exactamente a la mitad, entre el cero y el uno? Un medio. Si volviéramos a dividir el segmento de recta, exactamente a la mitad, entre 0 y un medio, y un medio y 1. Obtendríamos cuartos: un cuarto, dos cuartos, tres cuartos y nuestro entero.

Si dividimos cada cuarto exactamente a la mitad. Obtenemos octavos: un octavo, dos octavos, tres octavos, cuatro octavos, cinco octavos, seis octavos, siete octavos y nuestro entero.

Si dividimos cada octavo exactamente a la mitad obtendríamos dieciseisavos: un dieciseisavo, dos dieciseisavos, tres dieciseisavos … y así sucesivamente hasta llegar a nuestro entero.

Si dividimos cada dieciseisavo exactamente a la mitad obtendríamos un treintaidosavos.

Ahora sí, tomamos una fracción por ejemplo nueve dieciseisavos (9/16). ¿Cuál sería una fracción con menor valor de magnitud que esta fracción?

Una fracción con menor valor, puede ser: diecisiete treintaidosavos 17/32. Y una más pequeña diecinueve treintaidosavos (19/32).

¿Es posible continuar dividiendo cada treintaidosavo exactamente por la mitad? Sí es posible y obtendríamos sesentaicuatroavos.

Entonces ¿Por qué los racionales son densos? De acuerdo con las divisiones que hicimos, a cada segmento de recta, identificamos que dados dos números fraccionarios siempre encontraremos un número fraccionario entre ellos.  Esta propiedad está presente en los números fraccionarios y decimales.

Recapitulando:

Para identificar el numerador y el denominador de una fracción, puedes ver al primero como la cifra que numera la fracción y al segundo como la cifra que denomina las partes en las que está compuesta una unidad.

Para usar los signos mayor que y menor que, recuerda que: la apertura del signo siempre se colocará hacia el número mayor.

Estos temas los puedes localizar en tu Libro de secundaria de Matemáticas de primer grado.