diagrama de Árbol (probabilidad)

del libro de complemento mate mático pagina 136, del tema de probabilidad

Un diagrama de árbol es el dibujo que se usa para enumerar todos los resultados posibles de una serie de experimentos en donde cada experimento puede suceder en un número finito de maneras . ...

¿Qué es un árbol de decisiones?

Un árbol de decisiones (también llamados árbol de toma de decisiones, árbol de decisión o árboles de decisiones) es un esquema que representa las alternativas disponibles para quien va a tomar la decisión, además de las circunstancias y consecuencias de cada elección. Su nombre proviene del aspecto similar a un árbol y sus ramificaciones que tiene este diagrama.

Los árboles de decisiones están conformados por una serie de nodos de decisiones con ramas que llegan y salen de ellos. Estos nodos pueden ser:

Nodos Cuadrados o de decisión: Representan los puntos de decisión donde se muestran las distintas alternativas disponibles a elegir. Se escoge la alternativa que presenta el mayor valor esperado.
Nodos Circulares o de probabilidad: Donde salen las diferentes ramificaciones que muestran los hechos fortuitos que tienen una probabilidad de ocurrencia. La suma de las probabilidades de cada suceso (rama) que sale de un nodo circular debe ser uno. El valor esperado del nodo se obtiene realizando un promedio ponderado de las ramificaciones con sus probabilidades.
Nodos Terminales: Representan un resultado definitivo de una ramificación.

Las ramificaciones se representan de la siguiente forma:

Ramificaciones alternativas: Cada ramificación representa un resultado probable.
Alternativa rechazada: Una vez desarrollado el árbol, las alternativas que no se seleccionan se marcan con dos líneas.

Símbolos utilizados en un diagrama de árbol de decisiones

¿En qué tipo de decisiones se utiliza?

Este método se utiliza en una amplia gama de decisiones empresariales como:

Planificación de productos.
Análisis de procesos.
Capacidad de planta.
Alternativas de localización, entre otros.

¿Cómo hacer un diagrama de Árbol de decisiones?

Para crear un Árbol de Decisiones realizaremos los siguientes pasos:

Iniciar el árbol dibujando un nodo cuadrado que representa la decisión principal del problema.
Agregar las ramas y nodos que se presentarán en los posibles caminos que podemos elegir a partir del nodo de decisión inicial.
En los nodos de probabilidad, colocar los valores de probabilidad en cada rama.
Determinar los valores esperados de cada nodo terminal, teniendo en cuenta los gastos e ingresos esperados de cada camino.
Calcular los valores esperados de los nodos intermedios. Para el caso de los nodos de probabilidad se calcularán con un promedio ponderado y para los nodos de elección se elegirá la opción más conveniente de las disponibles.
Para el primer nodo (el de decisión), se elegirá el valor esperado más conveniente dependiendo de la decisión que se desea tomar.

ejemplo 1:El dueño de Hackers Computer Store analiza qué hará con su negocio en los próximos cinco años. El crecimiento de las ventas en años recientes ha sido bueno, pero crecerían sustantivamente si, como se ha propuesto, se construye una importante empresa electrónica en su zona. El dueño de Hackers ve tres opciones:La primera es ampliar su tienda actual, la segunda es ubicarla en otro lugar y la tercera es tan solo esperar y no hacer nada.

La expansión o la mudanza no tardaría mucho y, por lo mismo, la tienda no perdería ingresos. Si no hiciera nada en el primer año y hubiera un crecimiento notable, entonces consideraría la decisión de expandirse. Si espera más de un año, la competencia empezaría a llegar y provocaría que la expansión ya no fuera viable.

Los supuestos y circunstancias son:

Un crecimiento notable como consecuencia del incremento de la población de entusiastas de computadoras procedentes de la nueva empresa electrónica tiene una probabilidad de 55%.
Si crecimiento es notable en otro lugar, produciría un rendimiento anual de 195 000 dólares al año. Si el crecimiento es flojo en otro lugar significaría un rendimiento anual de 115 000 dólares.
Un crecimiento notable con una expansión produciría un rendimiento anual de 190 000 dólares al año. Si el crecimiento es flojo con una expansión significaría un rendimiento anual de 100 000 dólares.
En la tienda existente, sin cambio, el rendimiento anual sería de 170 000 dólares al año con un crecimiento notable y de 105 000 dólares con un crecimiento débil.
La expansión del local actual costaría 87 000 dólares.
Una mudanza costaría 210 000 dólares.
Si el crecimiento es notable y se amplía el local existente en el segundo año, el costo aún sería de 87 000 dólares.
Los costos de operaciones son iguales en todas las opciones.

Referencias:

Chase, R. & Jacobs, F. (2014). Administración de operaciones. Producción y cadena de suministro (Decimotercera ed.). Mexico, D.F.: McGraw-Hill.
Heizer, J., & Render, B. (2014). Principios de Administración de Operaciones (Novena ed.). Mexico, D.F.: Pearson Educación.
Krajewski, L., Ritzman, L. & Malhotra M, (2008). Administración de Operaciones. Procesos y Cadena de Valor (Octava ed.). Mexico, D.F.: Pearson Educación.

Para la construcción de un diagrama en árbol se partirá poniendo una rama para cada una de las posibilidades, acompañada de su probabilidad. ... El diagrama de árbol va de lo general a lo especifico, es decir, parte de un problema general (el “tronco”) y continua con niveles subsecuentes o causas (las “ramas”)

Árbol de probabilidad

Ir a la navegación Ir a la búsqueda

Un árbol de probabilidad o diagrama de árbol es una herramienta que se utiliza para determinar si en realidad en el cálculo de muchas opciones se requiere conocer el número de objetos que forman parte del espacio muestral, estos se pueden determinar con la construcción de un diagrama de árbol.

El diagrama de árbol es una representación gráfica de los posibles resultados del experimento, el cual consta de una serie de pasos, donde cada uno de estos tiene un número infinito de maneras de ser llevado a cabo. Se utiliza en los problemas de conteo y probabilidad.

Para la construcción de un diagrama en árbol se partirá poniendo una rama para cada una de las posibilidades, acompañada de su probabilidad. Cada una de estas ramas se conoce como rama de primera generación.

En el final de cada rama de primera generación se constituye, un nudo del cual parten nuevas ramas conocidas como ramas de segunda generación, según las posibilidades del siguiente paso, salvo si el nudo representa un posible final del experimento (nudo final).

Hay que tener en cuenta que la construcción de un árbol no depende de tener el mismo número de ramas de segunda generación que salen de cada rama de primera generación y que la suma de probabilidades de las ramas de cada nudo ha de dar 1.

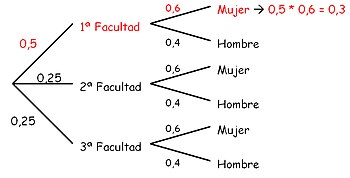
Existe un principio sencillo de los diagramas de árbol que hace que éstos sean mucho más útiles para los cálculos rápidos de probabilidad: multiplicamos las probabilidades si se trata de ramas adyacentes (contiguas), el ejemplo de alumna de la primera facultad, o bien las sumamos si se trata de ramas separadas que emergen de un mismo punto, el ejemplo de encontrar un alumno.