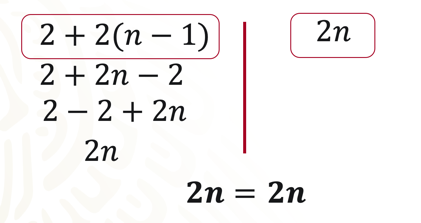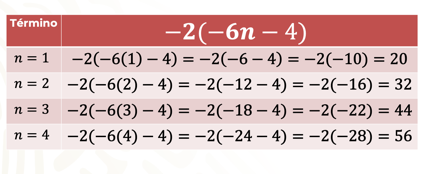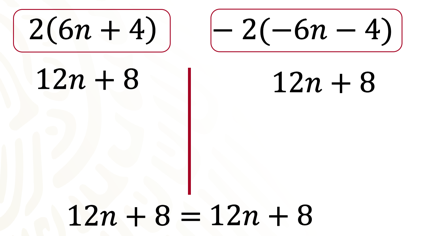primeros años De Lenguaje Común a Lenguaje Algebraico Ejemplos Resueltos

 

primeros años 

De Lenguaje Común a Lenguaje Algebraico Ejemplos Resueltos

¿Qué es el lenguaje algebraico?

El lenguaje algebraico es una forma de traducir a símbolos y números lo que normalmente conocemos como lenguaje natural. De esta forma se pueden manipular cantidades desconocidas con símbolos fáciles de escribir, lo que permite simplificar expresiones, formular ecuaciones e inecuaciones y permite el estudio de cómo resolverlas.

¿Para que sirve el lenguaje algebraico?

El lenguaje algebraico es utilizado para la representación de valores desconocidos, la principal función es estructurar un idioma que ayude a generalizar las diferentes operaciones que se desarrollan dentro de la aritmética. Ejemplo: si queremos sumar dos números cualesquiera basta con decir  x + y. 

Características del lenguaje algebraico.

• El lenguaje algebraico es más preciso que el lenguaje numérico: podemos expresar enunciados de una forma más breve.
• El lenguaje algebraico permite expresar relaciones y propiedades numéricas de carácter general.
• Con el lenguaje algebraico expresamos números desconocidos y realizamos operaciones aritméticas con ellos.

Ejemplos Resueltos de traducción de lenguaje verbal al lenguaje matematico ó lenguaje algebraico.

1. Un numero cualquiera: x

2. La suma de dos numeros diferentes: x + y

3. La diferencia de dos números: x - y

4. El producto de dos números: x y

5. El cociente de dos números: x/y

6. El cubo de un numero: x³

7. El triple del cuadrado de un numero: 3x²

8. La suma de los cuadrados de dos números: x² + y²

9. La quinta parte del cubo de un numero: x³/5

10. El cubo de la quinta parte de un numero: (x/5)³

11. La suma de dos números dividida entre su diferencia: (x + y)/(x - y)

12. ¿Cuál es el numero que agregado a 3 suma 8?: x + 3 = 8

13. ¿Cuál es el numero que disminuido de 20 da por diferencia 7?: x - 20 = 7

14. Las tres quintas partes de un numero aumentado en un cuarto: 3/5 x + 1/4
15. La diferencia entre un numero y su anterior: x - (x-1)
16. La suma entre un numero par y el triple del siguiente par: 2x + 3(2x+2)
17. El producto entre el doble de un numero y la tercera parte de su consecutivo: 2x·(x+1)/3
18. El cociente entre un numero y su mitad: x/(x/2)
19. La mitad de la suma de dos números multiplicado por el cuadrado de ambos números: 1/2·(x+y)(x·y)²
20. La raíz cubica del cuadrado de la suma de dos números: ³√(x+y)²
21. La tercera parte de un numero aumentado en 10: x/3 + 10
22. Las dos terceras partes de la suma de dos números: 2/3·(x+y)

Ejercicios de traducción de lenguaje común al lenguaje algebraico.
1) El doble de un número aumentado en la mitad del mismo número.
2) El doble de a, aumentado en b.
3) El doble de a aumentado en b.
4) La mitad de a más el triple de b.
5) El doble del cuadrado de a.
6) El cuadrado del doble de a.
7) La cuarta parte del triple del cuadrado de b.
8) El triple de la cuarta parte del cuadrado de b.
9) El cuadrado de la cuarta parte del triple de b.10) La diferencia entre el quintuple de x y la mitad de y.

11) La suma de tres números pares consecutivos.
12) Tres impares consecutivos.
13) La semisuma entre a y b.
14) La semidiferencia entre a y b.
15) El producto entre un numero y su antecesor.
16) El producto entre un numero y su sucesor.
17) El triple de un numero equivale al doble del mismo numero aumentado en quince.
18) La suma de los cuadrados de tres números consecutivos.
19) El volumen V de un cubo de arista (2a - 1)
20) La cuarta parte del producto entre el cuadrado de a y el cubo de b.

Lenguaje Algebraico Ejercicios Básicos Resueltos:

Lenguaje Algebraico
Lenguaje Común	Lenguaje Algebraico
Un número par cualquiera.	2x
Un número cualquiera aumentado en siete.	x + 7
La diferencia de dos números cualesquiera.	x - y
El doble de un número excedido en cinco.	2x + 5
La división de un número entero entre su antecesor	x/(x-1)
La mitad de un número.	d/2
El cuadrado de un número	x2
La semisuma de dos números	(x+y)/2
Las dos terceras partes de un número disminuidos en cinco es igual a 12.	2/3 (x-5) = 12
Tres números naturales consecutivos.	x, x + 1, x + 2.
La parte mayor de 1200, si la menor es w	1200 - w
El cuadrado de un número aumentado en siete.	a2 + 7
Las tres quintas partes de un número más la mitad de su consecutivo equivalen a tres.	3/5 p + 1/2 (p+1) = 3
El producto de un número positivo con su antecesor equivalen a 30.	x(x-1) = 30
El cubo de un número más el triple del cuadrado de dicho número.	x3 + 3x2
El doble de la diferencia de dos números.	2(x - y)
El triple de la suma de dos números.	3(x + y)
El denominador de una fracción, es cinco unidades menor que su numerador.	x/(x - 5)
En un terreno de forma rectangular, su ancho mide la mitad de su largo.	a = L/2
El ancho de un rectángulo es igual a las tres cuartas partes de su longitud.	a = 3/4 L
El numerador de una fracción excede al denominador en tres unidades.	(x+3)/x
La suma de tres números consecutivos.	x + (x+1) + (x+2)
El doble de la tercera potencia de x.	2x3

segundos años 21/10/2020 ¿Por qué son equivalentes?

 

segundos años

21/10/2020

¿Por qué son equivalentes?

Aprendizaje esperado: Verifica algebraicamente la equivalencia de expresiones de primer grado, formuladas a partir de sucesiones.

 

Énfasis: Explicar la equivalencia de las distintas expresiones algebraicas, cuando éstas representan la regla de una misma sucesión.

 

 

¿Qué vamos a aprender?

 

Profundizarás en la equivalencia de distintas expresiones algebraicas cuando éstas representan la regla general con la que se genera una misma sucesión.

 

En clases anteriores aprendiste a modelar la regla general de una sucesión, ya sea de figuras o de números. También analizaste que hay distintas maneras de expresar algebraicamente la regla de una misma sucesión y que todas ellas son equivalentes.

 

En esta sesión, construirás argumentos para explicar por qué dos o más reglas generales que modelan una misma sucesión son equivalentes. 

 

 

¿Qué hacemos?

 

Observa el siguiente video con la finalidad de analizar los argumentos y razonamientos de Emma y Mateo, alumnos de segundo de secundaria, al resolver una sucesión de figuras.

 

1. Reglas equivalentes de sucesiones.

https://www.youtube.com/watch?v=CyyY7bShbgY

 

Recupera los aspectos más relevantes del contenido del video:

 

Emma y Mateo se enfrentan a una tarea escolar que su maestra de Matemáticas les dejó realizar: conocer en qué lugar de la sucesión está ubicada la figura compuesta de 19 cuadrados en cada lado. Y, para ello, se ven en la necesidad de modelar la regla general de la sucesión.

 

Emma dice que se escriba el número del término de cada figura, y que “n” sea la letra que denote cada término de la sucesión, “n” es el enésimo término de la sucesión.

 

¿Qué significa el término enésimo de la sucesión?

 

El término enésimo se refiere a una cantidad que no puede determinarse de forma numérica. El concepto suele utilizarse para aludir a aquello que ocupa un sitio indefinido o impreciso.

 

En matemáticas, el término enésimo de una sucesión significa que ese término representa cualquier lugar que ocupe una figura en la sucesión. Es decir, figura 1, figura 2, figura 3, y así sucesivamente; por esta razón, se dice figura “n”, refiriéndose a cualquier figura que sea modelada con la misma regla que las anteriores.

 

Aclarado lo anterior, retoma la regla general de la sucesión que establecen Mateo y Emma.

 

Regla general de Mateo

 

 

Mateo obtiene la regla general a partir de los significados que él le asocia a la construcción de cada figura según el término que ocupa en la sucesión. Es decir, analiza cómo está construida cada figura.

 

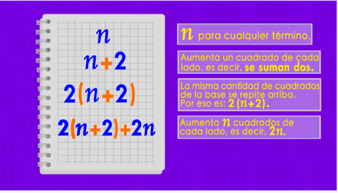
Es necesario partir de la cantidad de cuadrados que tiene cada término. El término 1 tiene 1 cuadrado, por ello, establece la igualdad:

 

n = 1, n = 2, n = 3, y así sucesivamente.

 

Él sabe que a cada término se le aumentan dos cuadrados, uno de cada lado, por ello generaliza que se suman 2; se tiene la expresión:

 

n + 2

 

Después, identifica que existen la misma cantidad de cuadrados de la base y de lo que él llama “arriba”, por ello establece la expresión:

 

2(n + 2)

 

Finalmente, identifica que para los lados de la derecha y de la izquierda se aumentan n cuadrados de cada lado, por eso afirma que su regla general es:

 

2(n + 2) + 2n

 

Regla general de Emma

 

Emma realizó el conteo de los cuadrados que tiene cada figura de la sucesión. Ella sabe que en la primera figura hay 8 cuadrados, 12 en la segunda y 16 en la tercera.

 

Con ello estableció la sucesión:

 

8, 12, 16…

 

Emma identificó la constante aditiva, que es 4. Es decir, “para pasar del primer al segundo término, se suma 4 y así sucesivamente”.

 

La regla general de Emma es:

 

8 + 4(n - 1)

 

Consideró 8 porque esa es la cantidad de cuadrados que tiene el primer término, y cada término posterior es el anterior más 4

 

Por lo tanto, ambas reglas son correctas.

 

¿Por qué ambas reglas son correctas?

 

¿Cómo se puede comprobar que las dos reglas son equivalentes?

 

A continuación, retoma los argumentos que dieron Emma y Mateo:

 

Lo que Emma y Mateo hicieron, fue transformar las reglas generales, 2(n + 2) + 2n y 8 + 4(n – 1) al realizar las operaciones algebraicas.

 

 

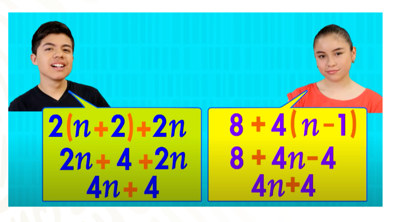
Al multiplicar el binomio 2(n + 2), y considerando la jerarquía de las operaciones, se pueden dejar de usar los paréntesis, así el producto obtenido transforma las expresiones algebraicas en equivalentes.

 

2(n + 2) + 2n = 2n + 4 + 2n

 

Al sumar términos semejantes, también se tienen expresiones algebraicas equivalentes:

 

2(n + 2) + 2n = 2n + 4 + 2n = 4n + 4

 

Este proceso también lo realiza Emma:

 

Ella multiplica el binomio 4(n-1) y obtiene:

 

8 + 4(n – 1) = 8 + 4n – 4

 

Al sumar términos semejantes, también se tienen expresiones algebraicas equivalentes:

 

8 + 4(n – 1) = 8 + 4n – 4 = 4n + 4

 

Ahora sabes que lo que significa la equivalencia entre reglas generales que modelan la misma sucesión.

 

A continuación, analiza la siguiente explicación:

 

Al analizar una sucesión numérica para encontrar la expresión algebraica de la regla, es posible encontrar más de una expresión algebraica equivalente.

 

Dos expresiones algebraicas son equivalentes cuando se cumple la igualdad entre ambas expresiones y se puede comprobar numéricamente cuando se le asigna cualquier valor a las literales que intervienen.

 

Por ejemplo:

 

3n + 6 es equivalente a 3(n + 2), porque al asignar un valor a “n”, por ejemplo 5, las dos expresiones dan el mismo resultado:

 

3n + 6 = 3(5) + 6 = 15 + 6 = 21

 

3(n + 2) = 3(5 + 2) = 3(7) = 21

 

En la transformación de expresiones equivalentes es importante que:

 

1. Al sumar consideres las siguientes propiedades:

 

• Conmutativa: 3a + b = b + 3a
• Asociativa: (3a + b) + c = 3a + (b + c) = 3a + b + c
• Del neutro aditivo: 3a + 0 = 3a
• Del inverso aditivo: 3a – b = 3a + (–b)

 

2. Y al multiplicar consideres estas otras propiedades:

 

• Conmutativa 3ab = 3ba
• Asociativa (3ab) c = 3a(bc)
• Distributiva 3a (b + c) = (3ab) + (3ac)
• Y del neutro multiplicativo 1 x 3a = 3a

 

Ahora, retoma el problema de la sesión anterior.

 

Problema. Estanques de diversos tamaños

 

En un parque ecológico se planea construir estanques de diversos tamaños. El borde de cada uno estará formado por losetas cuadradas, como se muestra en la figura.

 

 

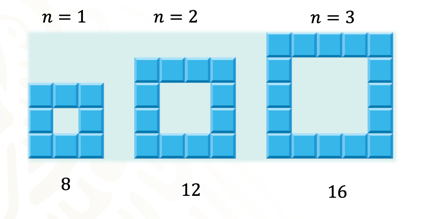
Asimismo, se estableció que las reglas generales: n4 + 4 y 4(n + 1) que modelan la situación son equivalentes.

 

 

Después, se comprobó al asignar valores numéricos para determinar los seis primeros términos de la sucesión

 

8, 12, 16, 20, 24…

 

Ahora, realizarás la trasformación de las expresiones algebraicas.

 

Dada la regla general n4 + 4 que representa la sucesión 8, 12, 16, 20, 24

 

Se sabe que, al aplicar la propiedad para la multiplicación que dice: “el orden de los factores no altera el producto”, se obtiene lo siguiente:

 

ab = ba

 

Si “a” es “n”, y “b” es 4, se tiene n4 = 4n

 

 

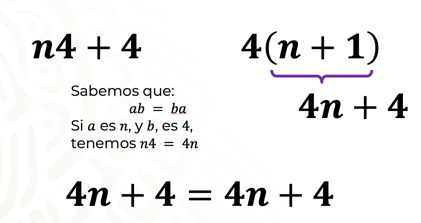
La regla queda: 4n + 4

 

Dada la regla general 4 (n + 1), que representa la sucesión 8, 12, 16, 20, 24, se multiplica el binomio 4(n + 1), cuyo producto queda: 4n + 4

 

Por lo tanto, las reglas generales son equivalentes.

 

Ahora, retoma otro problema de la sesión anterior.

 

Problema Raquel y Lía

 

El juego de Raquel y Lía, quienes, por turnos, se mostraron tarjetas con sucesiones numéricas y una expresión algebraica que las representa; la jugadora contraria escribió una expresión algebraica equivalente a la que estaba en la tarjeta.

 

Con ambas expresiones algebraicas obtienes el mismo resultado, ya que calculaste los seis primeros términos de la sucesión.

 

Observa las reglas generales establecidas:

 

• Se tiene la sucesión “A”: 3, 5, 7, 9, 11, 13…

 

• La primera regla: 3 + 2(n-1), y la segunda regla 3+[(2)(n) -2]

 

Realiza la trasformación algebraica de las reglas.

 

Tienes la regla: 3 + 2(n – 1), que modela la sucesión A: 3, 5, 7, 9

 

Al multiplicar por 2 el binomio (n - 1) obtienes:

 

3 + (2n – 2)

 

La expresión ya no se puede simplificar, ya que si divides el binomio (2n - 2) entre 2, obtendrías la expresión 3 + (n - 1), la cual ya no modela la sucesión A

 

Ahora la regla: 3 + [(2)(n)-2], que modela la sucesión A: 3, 5, 7, 9…

 

Aplicando la jerarquía de las operaciones, efectúa las operaciones que están dentro de los paréntesis, por lo que debes multiplicar a 2 por n, y obtienes 2n

 

3 + [2n - 2]

 

Con las expresiones anteriores de las reglas 1 y 2 que obtuviste, sabes que los corchetes y los paréntesis tienen la misma función. Por lo tanto:

 

 

Has aprendido que una sucesión puede tener al menos dos expresiones algebraicas que las modelen correctamente, y que dichas expresiones algebraicas son equivalentes.

 

Además, que esta equivalencia se puede verificar al transformar las expresiones algebraicas.

 

Observa un ejemplo más.

 

Problema Raquel y Lía 2

 

Observa las reglas generales establecidas por Raquel y Lía para la sucesión B: 2, 4, 6, 8…

 

Se tiene la regla general: 2 + 2(n – 1) y la regla general: 2n

 

¿Qué identificas en estas reglas generales?

 

Ya sabes que con ambas expresiones algebraicas obtienes el mismo resultado, ya que se calcularon los seis primeros términos de la sucesión.

 

 

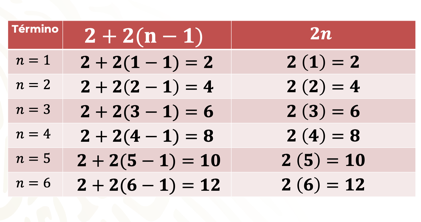
¿Qué identificas en estas reglas generales?

2 + 2(n – 1) y 2n

 

La regla 2n ya no puede transformarse en una más sencilla o simplificarse.

 

Lo que comprobarás es que, la regla 2 + 2(n – 1) sea equivalente a 2n

 

Regla: 2+ 2(n – 1), que modela la sucesión B: 2, 4, 6, 8…

 

Al multiplicar 2 por el binomio (n - 1), se tiene:

 

2 + 2n – 2

 

Se reducen términos semejantes y la expresión queda como: 2n

 

 

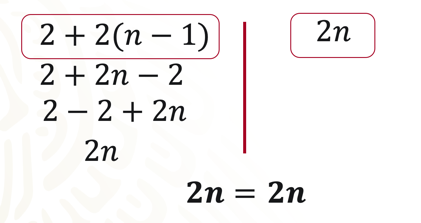
Por lo tanto, 2n = 2n

 

En la sucesión de 20, 32, 44, 56… las reglas 2(6n+4) = −2(−6n−4) son equivalentes porque se determinan los cuatro primeros números de cada una de las reglas para saber si pertenecen a la sucesión.

 

Al sustituir los primeros cuatro términos en la regla, puedes observar que sí corresponden a la sucesión: 20, 32, 44, 56…

 

 

En la regla −2(−6n−4), al sustituir los primeros términos, puedes observar que los resultados sí corresponden a la sucesión dada: 20, 32, 44, 56…

 

 

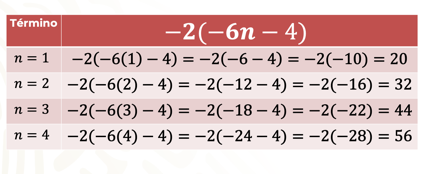
Ahora aplica lo aprendido:

 

En la sucesión de 20, 32, 44, 56… las reglas 2(6n+4) y −2(−6n−4) son equivalentes porque, al realizar la trasformación algebraica a través de la multiplicación del binomio por el factor correspondiente, obtienes expresiones que son iguales.

 

 

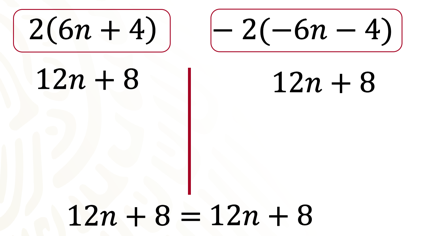
Para la sucesión −3, −7, −11, −15, −19…, cuya regla es: -4n + 1, ¿cuál de las siguientes sucesiones son equivalentes?

 

 

En esta clase adquiriste argumentos para explicar la equivalencia de las distintas expresiones algebraicas cuando éstas representan la regla de una misma sucesión.

 

Recuerda que este es un material de apoyo y que puedes consultar otras fuentes para complementar lo que aprendan aquí.

 

Revisa y practica lo aprendido, puedes consultar tu libro de texto de Matemáticas de segundo grado.