SEGUNDOS AÑOS
15/10/2020
Resolución de problemas mediante un sistema de ecuaciones lineales
Aprendizaje esperado: Resuelve problemas mediante la formulación y solución algebraica de sistemas de dos ecuaciones lineales con dos incógnitas.
Énfasis: Resolver problemas mediante sistemas de dos ecuaciones lineales con dos incógnitas, utilizando diferentes métodos de solución.
¿Qué vamos a aprender?
Repasarás lo que has aprendido en las últimas sesiones, con respecto a cómo resolver algunos problemas mediante el sistema de dos ecuaciones lineales con dos incógnitas.
Has estudiado cuatro métodos: el método gráfico, el método de igualación, el método de sustitución y el método de suma y resta, también llamado de eliminación. También has utilizado en cada método las propiedades de los números y las operaciones para la resolución de los problemas.
En esta sesión, resolverás algunos problemas mediante sistemas de dos ecuaciones lineales con dos incógnitas, utilizando diferentes métodos de solución.
¿Qué hacemos?
Resuelve el siguiente problema sobre costos de dulces:
Problema sobre costos de dulces
Armando y Gabriela son hermanos, ayer por la mañana, Armando fue a una tienda cercana a su casa, compró 3 chocolates y una paleta pulpa-mango, en total le cobraron $19.
Más tarde, Gabriela compró en la misma tienda un chocolate y una paleta pulpa-mango, pagando un total de 9 pesos.
¿Cuánto cuesta cada dulce?
¿Cómo puedes saber el precio de un chocolate y de una paleta pulpa-mango?
Para resolver el problema, es necesario modelar matemáticamente los datos; en este caso, primero definirás las literales que representarán a cada uno de los datos desconocidos.
Se representará el costo de los chocolates con la literal “x”, y al costo de las paletas con la literal “y”, estas literales serán las incógnitas.
Armando compró 3 chocolates y una paleta pulpa-mango, en total le cobraron 19 pesos; la ecuación que representa estos datos es:
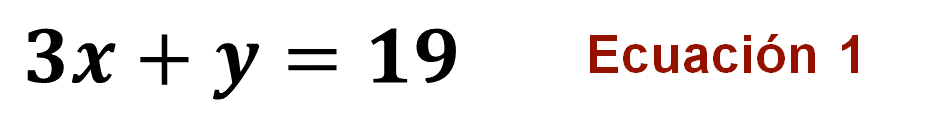
Por otra parte, Gabriela compró un chocolate y una paleta pulpa-mango, pagando un total de 9 pesos, la ecuación que representa estos datos es:

El sistema de ecuaciones lineales queda integrado de la siguiente manera:
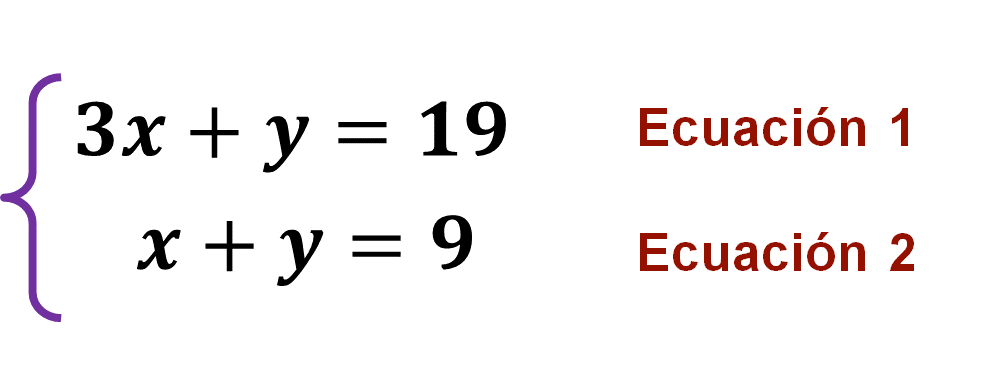
La llave se usa para indicar que ambas ecuaciones forman un sistema, cuya solución son los valores de la literal “x” y de la literal “y”, que hacen válidas ambas igualdades de manera simultánea.
Para dar respuesta a la pregunta planteada en el problema, resolverás el sistema de ecuaciones lineales 2x2.
De los cuatro métodos que has estudiado: el método gráfico, el método de sustitución, el método de igualación y el método de suma y resta:
¿Qué método consideras que sea más pertinente para resolver el sistema de ecuaciones lineales 2x2?
Inicia con la resolución del problema propuesto utilizando el método gráfico.
Método Gráfico
Recuerda que el método gráfico consiste en despejar a la literal “y” en ambas ecuaciones, para después tabular y graficar cada una de éstas, siendo las coordenadas del punto de intersección de las rectas obtenidas la solución del sistema.
1. Despeja “y” en ambas ecuaciones.
Revisa cómo quedan los despejes de la literal “y” en cada una de las dos ecuaciones que forman el sistema de ecuaciones lineales planteado, para resolver el problema de Gabriela y Armando.
En la ecuación uno el despeje de “y” queda de la siguiente forma:

Y el despeje de “y” en la ecuación dos, queda:

El sistema de ecuaciones queda:

2. Procede con la tabulación de cada igualdad asignando valores a “x” para determinar valores de “y” y formar pares ordenados (x, y).
Los valores que satisfacen la relación planteada en cada igualdad se escriben en la última columna de cada una de las tablas como un par ordenado (x, y). Estos pares ordenados, representan puntos en el plano cartesiano.

Una vez que las tablas de los valores que representan a los pares ordenados este completa, procederás a ubicar en el plano cartesiano los puntos, por los cuales puedes trazar las dos líneas rectas que caracterizan el gráfico de este sistema de ecuaciones lineales.
3. Grafica las coordenadas. El resultado de graficar una ecuación de primer grado es una línea recta. Las coordenadas del punto donde unen las dos líneas rectas son la solución del sistema.
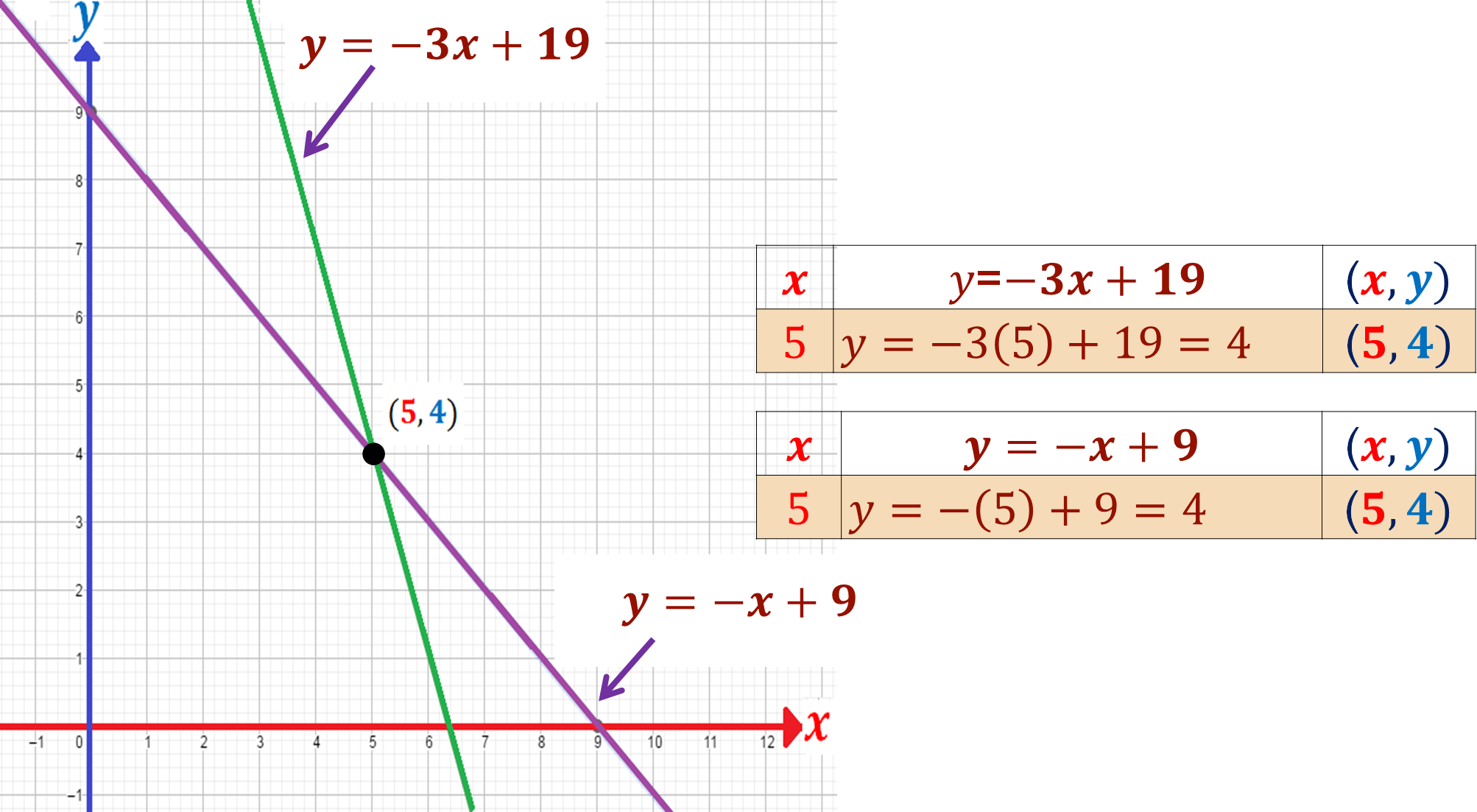
Es importante que, al graficar los datos registrados en la tabulación de cada una de las ecuaciones en un mismo plano cartesiano, se realice una correcta graduación en los ejes y una correcta posición en el trazado, de ello depende que se pueda identificar claramente el resultado correcto. Por eso se recomienda usar libreta cuadriculada, o bien, papel milimétrico.
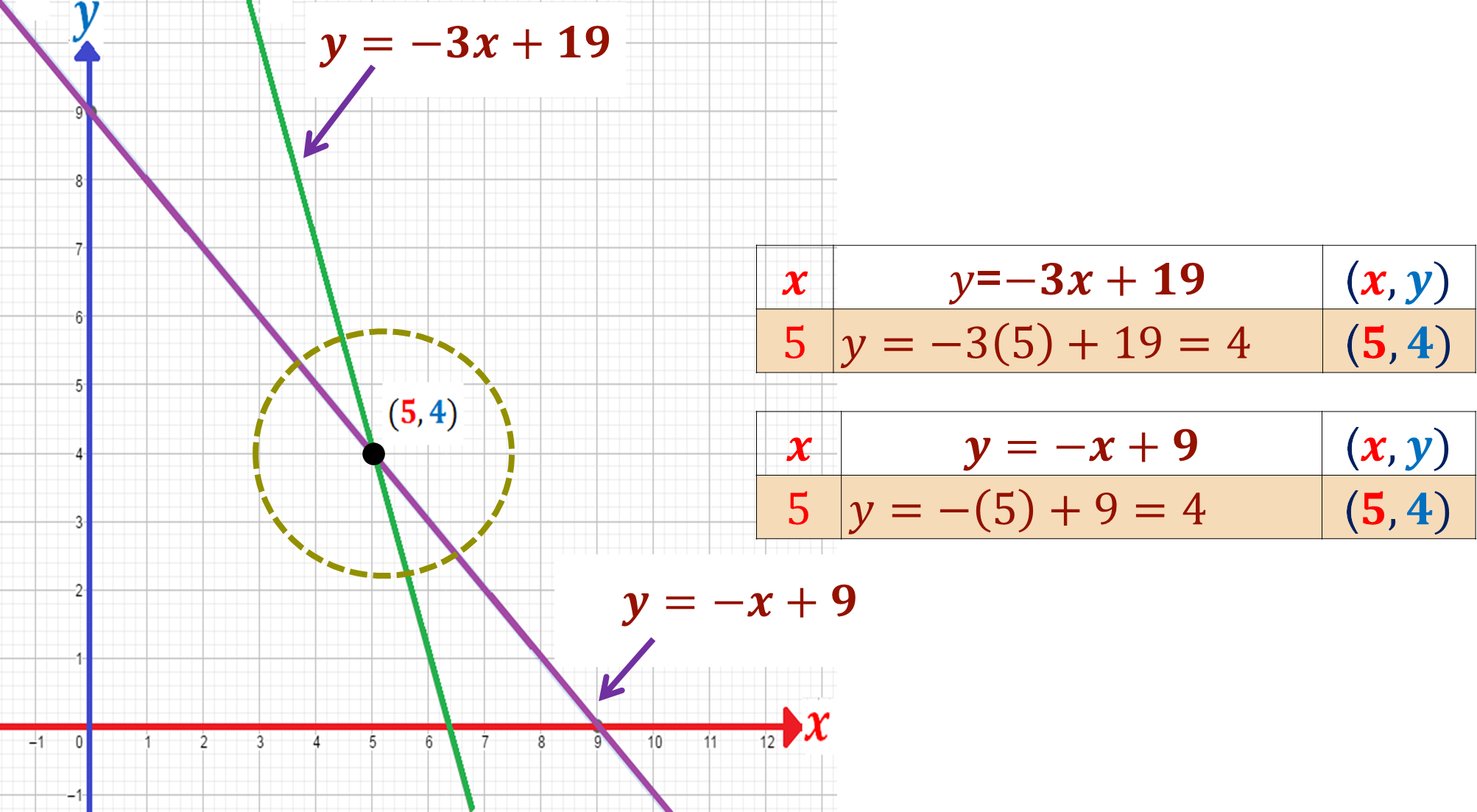
En un sistema de ecuaciones lineales, puede ocurrir que las rectas se crucen, en este sistema sí sucede así, se cortan las dos rectas en el punto (5, 4), entonces la solución al sistema es:
x=5
y=4
Observa que las coordenadas del punto donde se cortan las dos líneas rectas son la solución del sistema. Se sabe que en la primera ecuación cuando x =5, y=4. Y en la segunda ecuación, cuando x=5, y=4.
¿Qué dato representa la incógnita “x”, y cuál representa la incógnita “y”?
La literal “x” se utiliza para representar el costo de un chocolate y la literal “y” se utiliza para representar el costo de una paleta pulpa-mango. De esta manera se puede responder la pregunta:
¿Cuál es el costo de cada dulce?
Un chocolate cuesta 5 pesos y una paleta pulpa-mango cuesta 4 pesos.
¿Si se resuelve el sistema de dos ecuaciones lineales con otro método, obtendrás el mismo resultado?
Observa qué sucede con el método de igualación.
Método de Igualación
Utiliza el sistema de ecuaciones que previamente usaste:
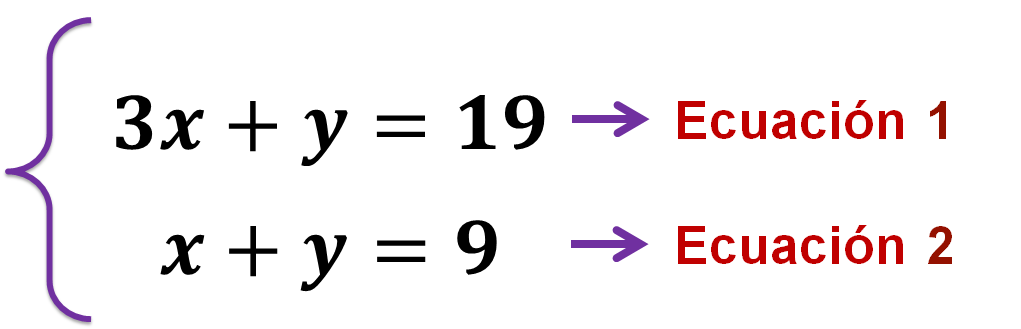
Ahora, el primer paso en el método de igualación consiste en despejar la misma incógnita en ambas ecuaciones.
Para decidir qué incógnita es conveniente despejar, es necesario analizar con detenimiento las características de cada ecuación.
La literal “y” tiene coeficiente uno en ambas ecuaciones, esto es una ventaja; por lo anterior, es recomendable despejar la literal “y” en las dos ecuaciones.
Despeja la misma incógnita en ambas ecuaciones:
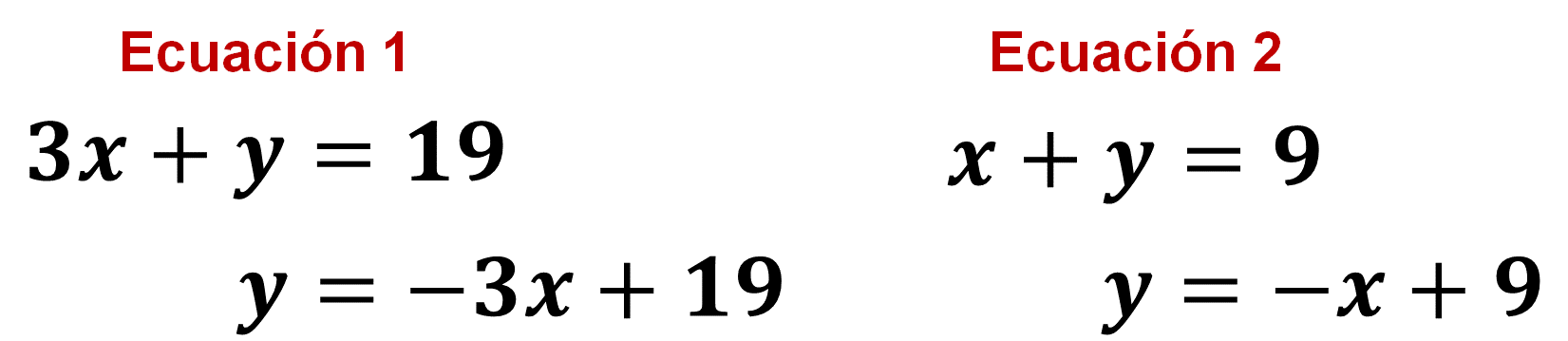
Ahora procederás a igualar las expresiones algebraicas obtenidas de los despejes, de esta forma obtendrás una nueva ecuación lineal con una sola incógnita. Así queda formada la ecuación:
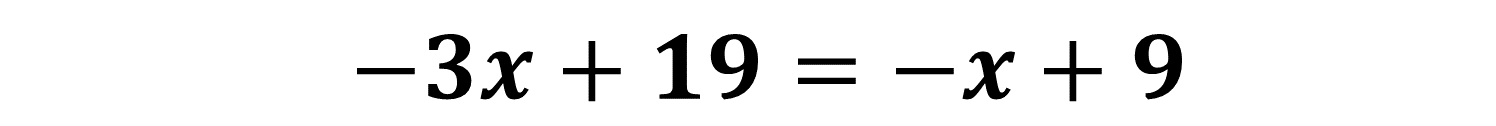
Ahora resuelve la ecuación lineal obtenida.
Para resolver esta ecuación, agruparás los términos algebraicos semejantes en un lado de la igualdad y en el otro lado los términos numéricos, continua con la reducción de términos, tanto algebraicos como numéricos, para encontrar el valor de la primera incógnita:
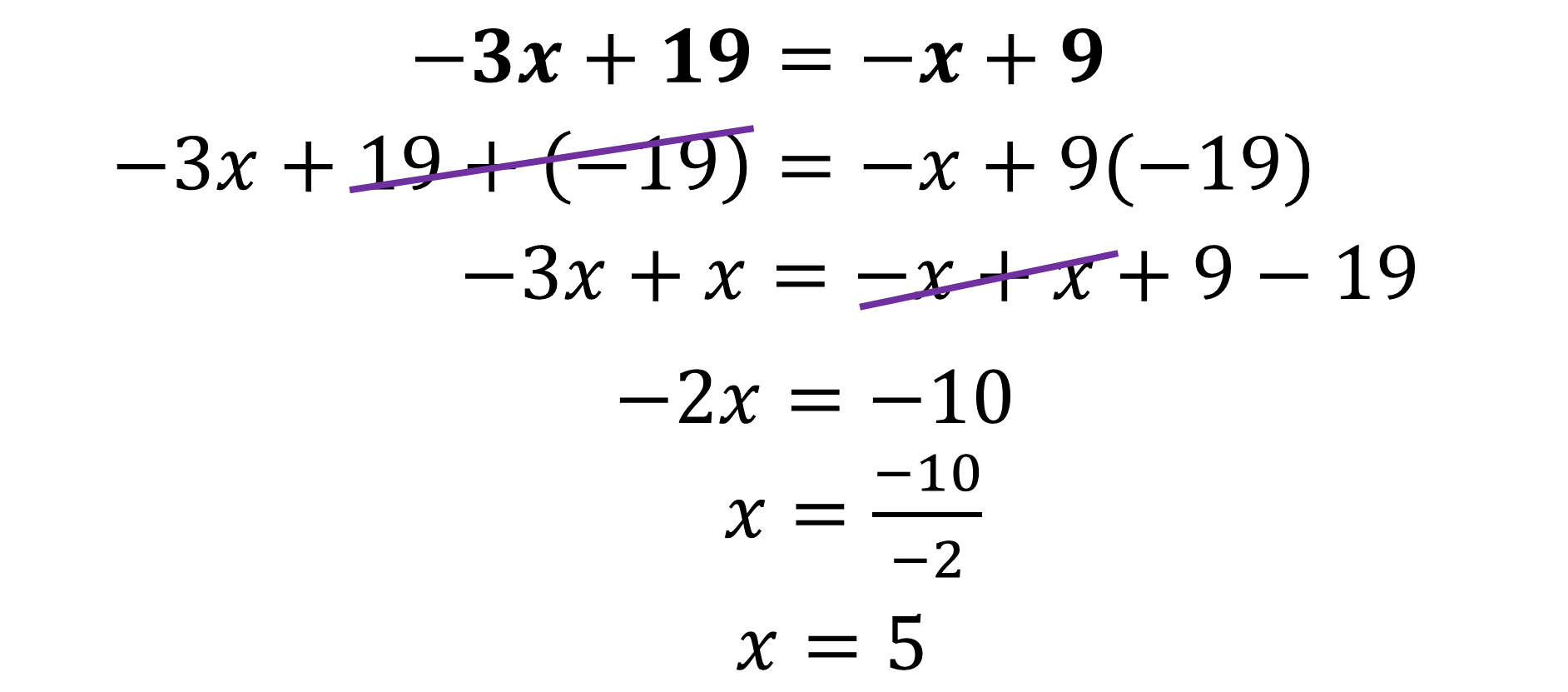
En este caso x=5.
Después, el valor obtenido de x=5, se sustituye en cualquiera de las dos ecuaciones originales, para determinar el valor de la literal “y”.
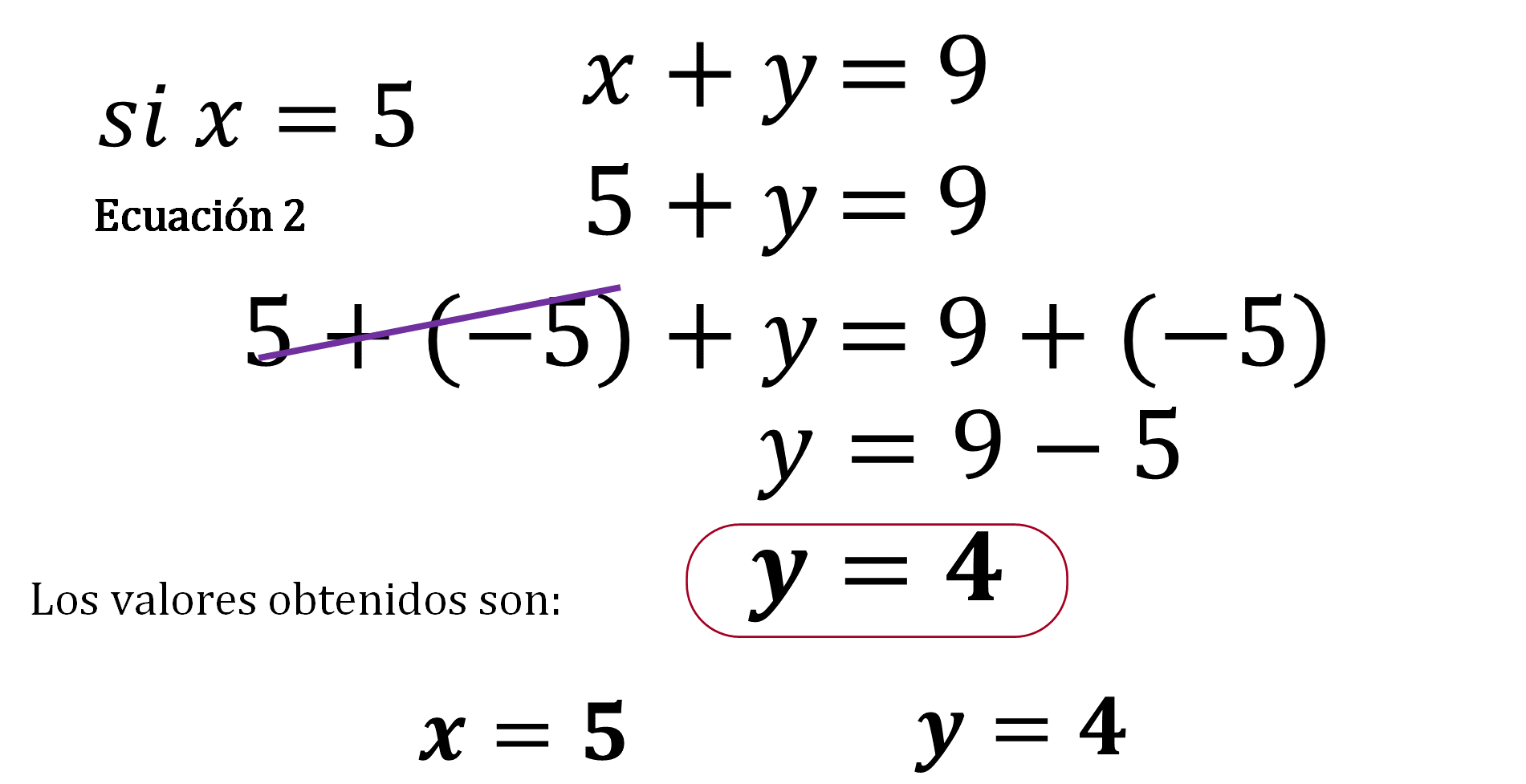
En este caso, sustituiste en la ecuación original número dos, por ser la más sencilla, y de esta manera se encontró que: y=4
Tomando en cuenta que la literal “x” representa el costo de un chocolate y la literal “y” el costo de una paleta pulpa-mango. Ahora sabes que un chocolate cuesta 5 pesos, y una paleta pulpa-mango cuesta 4 pesos.
Hasta ahora has resuelto el sistema de dos ecuaciones lineales con dos incógnitas utilizando dos métodos diferentes; el método gráfico y el método de igualación. Y obtuviste el mismo resultado.
Resuelve el mismo sistema utilizando el método de sustitución, y verifica si se obtienen los mismos resultados.
Método de Sustitución
El método de sustitución consiste en despejar una de las incógnitas en cualquiera de las dos ecuaciones, y luego sustituir el valor algebraico en la otra ecuación, de esta manera se obtiene una ecuación lineal que permite encontrar el valor numérico de una de las incógnitas para después hallar el valor de la otra incógnita.
Utiliza el sistema de ecuaciones:
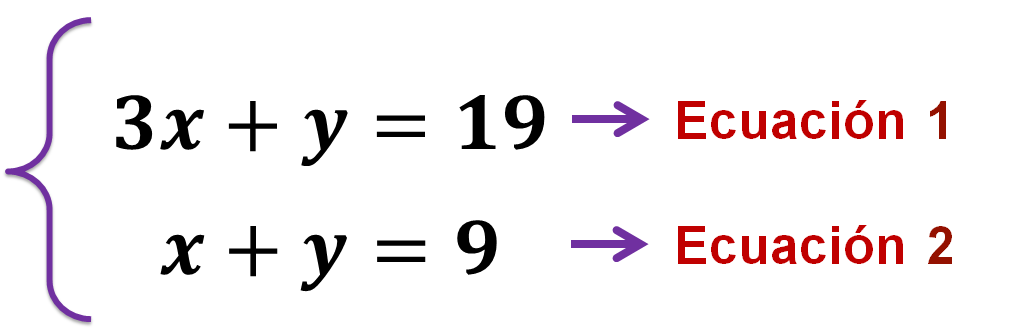
Para decidir cuál de las incógnitas despejar y en cuál de las ecuaciones hacerlo, es necesario observar los coeficientes de cada literal, esto será un referente para decidir en cuál es más conveniente.
En esta ocasión despejarás la literal “y”, en la ecuación: x + y = 9
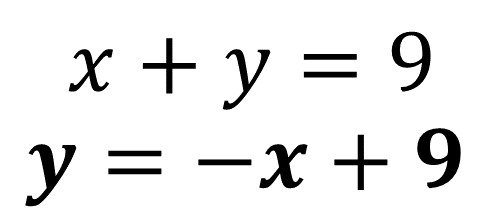
Quedando el despeje, y = -x + 9
Posteriormente sustituirás en la otra ecuación el valor algebraico de la literal “y”, recuerda que la sustitución nunca debe realizarse en la misma ecuación de donde se obtuvo el despeje.
Como el despeje de “y” se hizo en la ecuación dos, entonces la sustitución la realizarás en la ecuación uno, es decir, en:
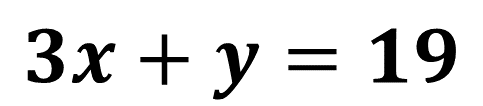
Ahora, sustituye la literal “y” en la ecuación:
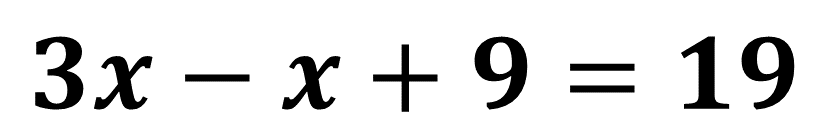
Observa que la ecuación tiene ahora una sola incógnita
A continuación, resuelve la ecuación:
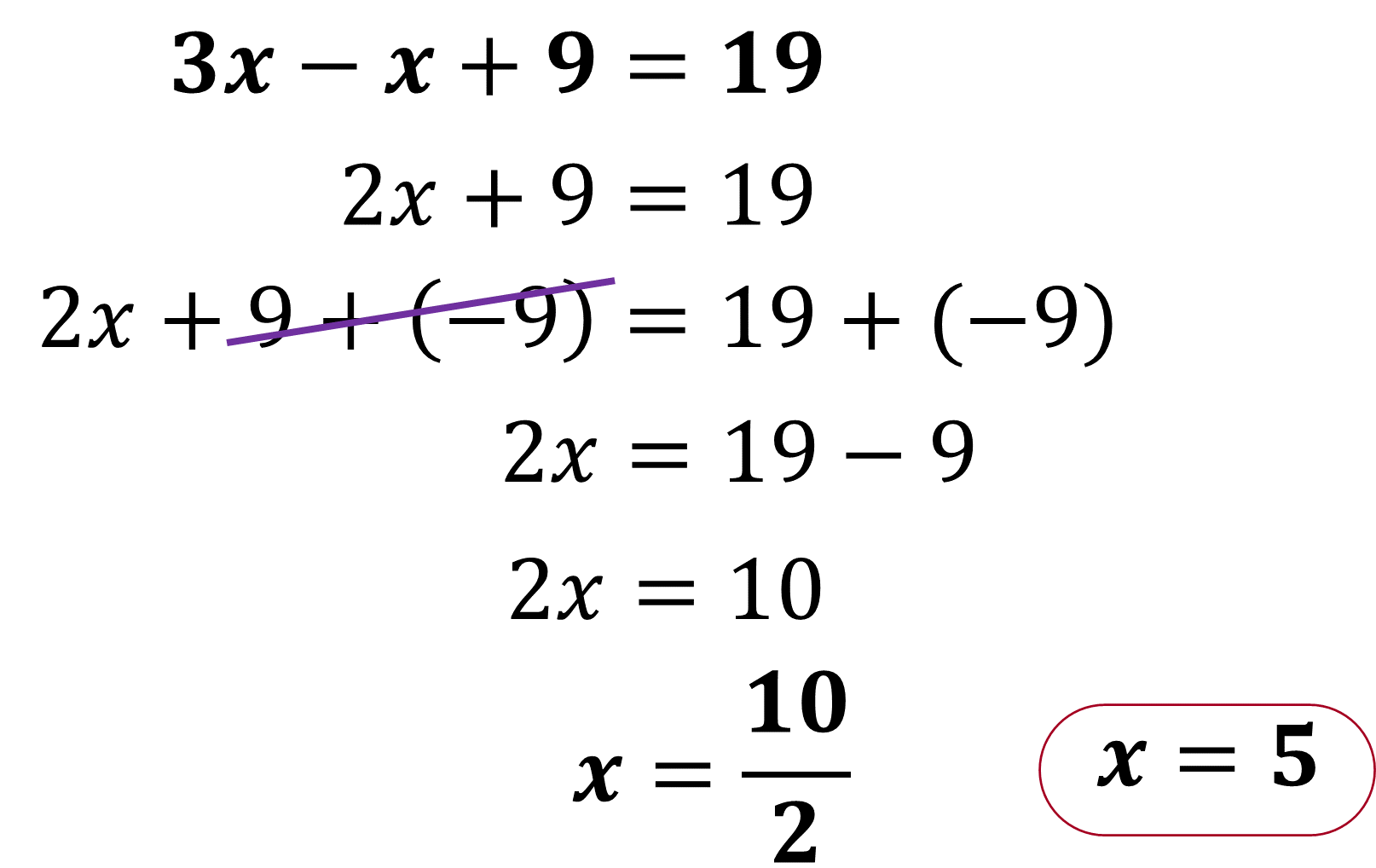
Por último, el valor numérico encontrado de la literal “x”, es decir: x=5, se sustituye en una de las dos ecuaciones originales para encontrar el valor numérico de la literal “y”:
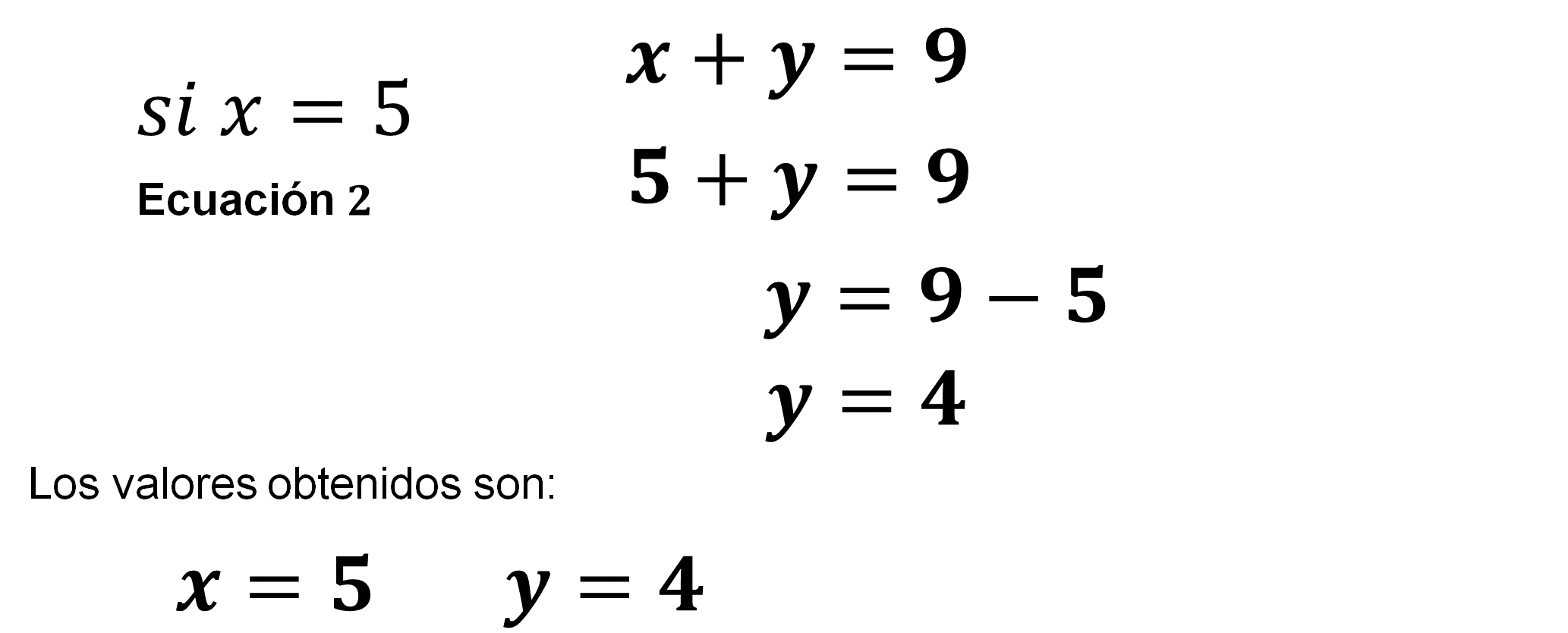
“y” es igual a cuatro.
La literal “x” representa el costo de un chocolate y la literal “y” el costo de una paleta de pulpa-mango. Entonces se puede confirmar que un chocolate cuesta 5 pesos y una paleta pulpa-mango cuesta 4 pesos.
Hasta ahora has utilizado tres métodos diferentes y en los tres obtuviste el mismo resultado.
¿Llegarás al mismo resultado si se resuelve el sistema de ecuaciones con el método de suma y resta, o de eliminación?
Observa qué sucede si utilizas el método de suma y resta, también llamado, método de eliminación.
Método de Suma y Resta
Para resolver un sistema de dos ecuaciones lineales utilizando el método de suma y resta, es necesario en primer lugar verificar que los términos de las ecuaciones tengan la forma: ax+by=c.
El sistema de ecuaciones lineales planteado con base en el problema de Armando y Gabriela es:
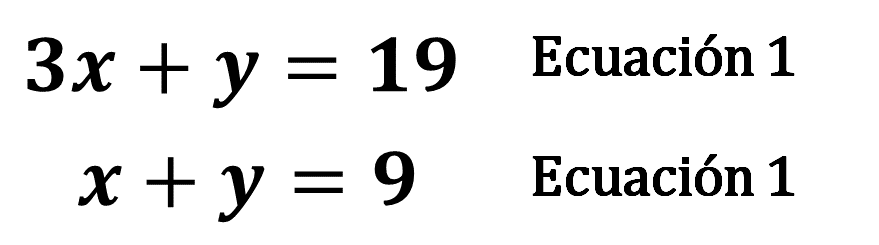
En el sistema ambas ecuaciones están de la forma ax+by=c., por lo que no es necesario hacer algún acomodo de términos.
El método de suma y resta consiste en eliminar una de las incógnitas mediante una suma y resta de los términos numéricos y algebraicos de ambas ecuaciones.
Para esto es necesario que los coeficientes numéricos de una de las incógnitas tengan el mismo valor absoluto, pero que sean simétricos, es decir, que uno sea positivo y el otro negativo.
Ahora, se igualan los valores absolutos de los coeficientes de la literal (incógnita) que se va a eliminar. Si observas el sistema, contiene coeficientes con el mismo valor absoluto en la incógnita “y”, por lo tanto, se procede a aplicar el simétrico, es decir, multiplicar por uno negativo a cada término y en ambos lados de la ecuación dos:
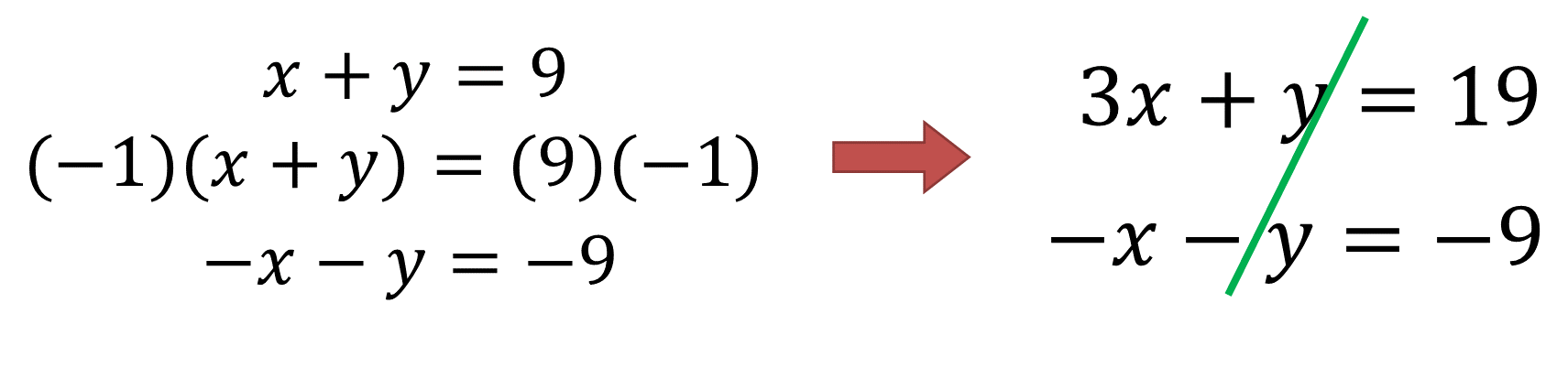
Observa que el coeficiente de la literal “y” en una de las dos ecuaciones, es positivo y en la otra es negativo, esto te permitirá que al sumar ambas ecuaciones puedas eliminar la incógnita “y”, resultando una ecuación con una sola incógnita:
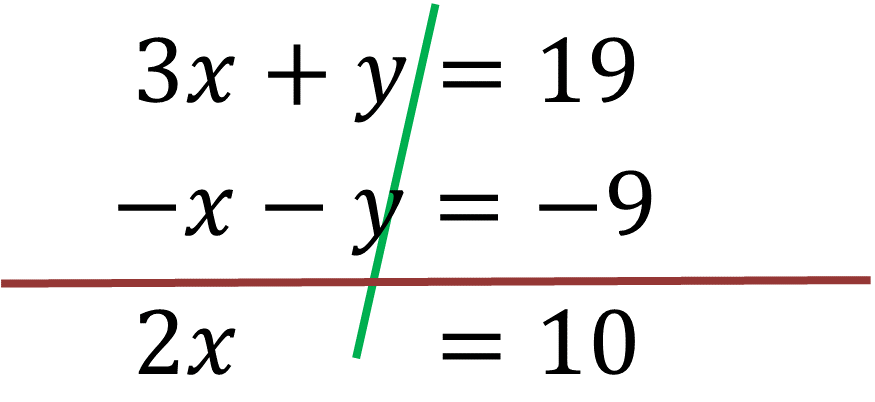
Posteriormente se resuelve la ecuación con una incógnita que resultó de la suma de las ecuaciones, y se obtiene el valor de la incógnita.
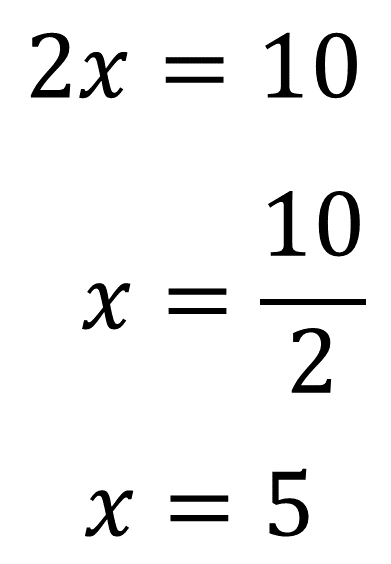
Por lo tanto, obtienes el valor de “x”. Es decir, x=5.
Ahora, sustituye el valor hallado en cualquiera de las ecuaciones originales, para encontrar el valor de la otra incógnita.
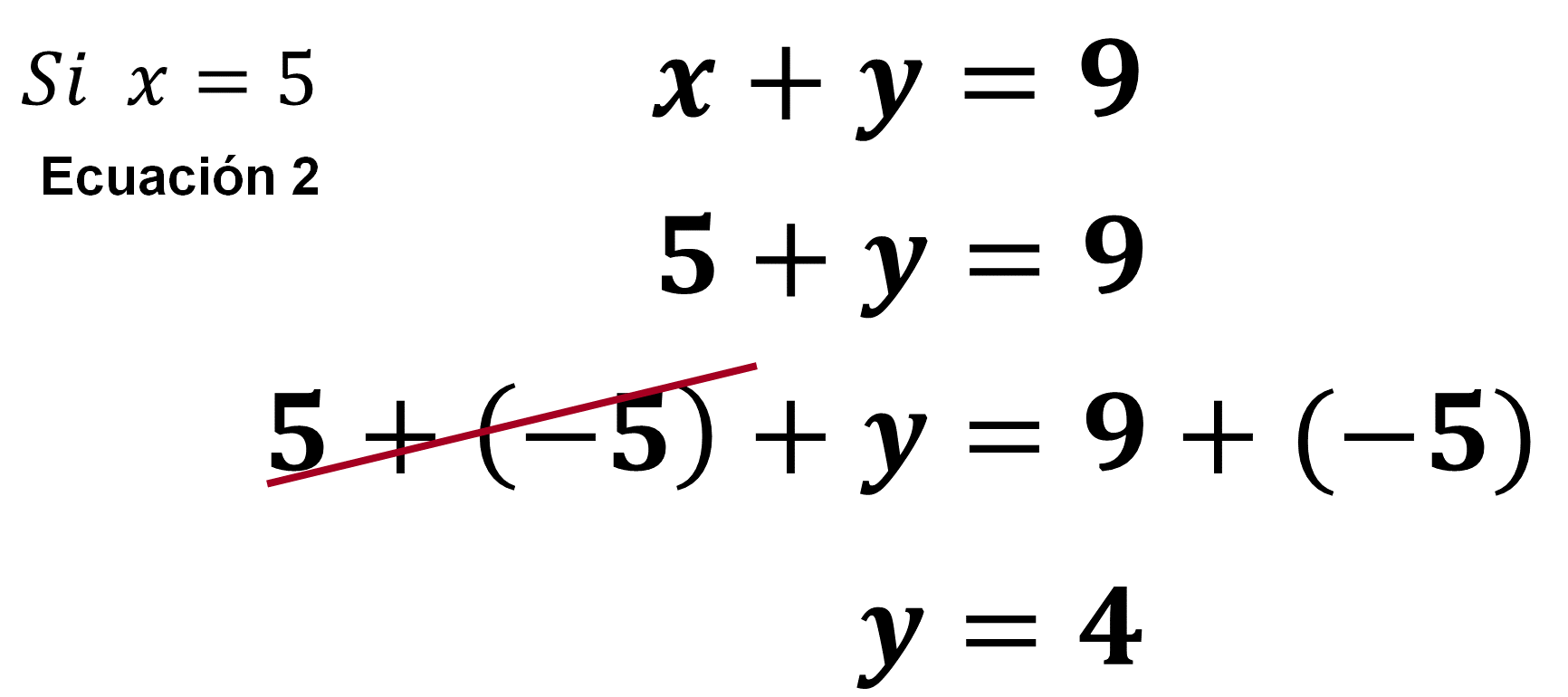
Así encuentras que el valor de la literal “y” es igual a 4.
Como pudiste darte cuenta, para conocer el precio de cada chocolate y de la paleta pulpa-mango, en el problema de Armando y Gabriela, tuviste que plantear un sistema de ecuaciones lineales 2x2, además has utilizado cuatro métodos diferentes para su resolución, obteniendo los mismos valores numéricos para las literales que eran las incógnitas.
Ya sabes que el costo de un chocolate es de cinco pesos y el costo de una paleta pulpa-mango es de cuatro pesos. Sin embargo, es necesario verificar que dichos valores satisfacen ambas ecuaciones.
Resolver una ecuación es hallar el valor o valores de la(s) incógnita(s) de manera que la igualdad sea cierta.
Comprobar que la igualdad se cumple, consiste en remplazar los valores obtenidos en cada una de las dos ecuaciones originales que integran el sistema.
Sustituye los valores de “x” y “y”, y procede a comprobar respetando la jerarquía de operaciones.
Comprobación:
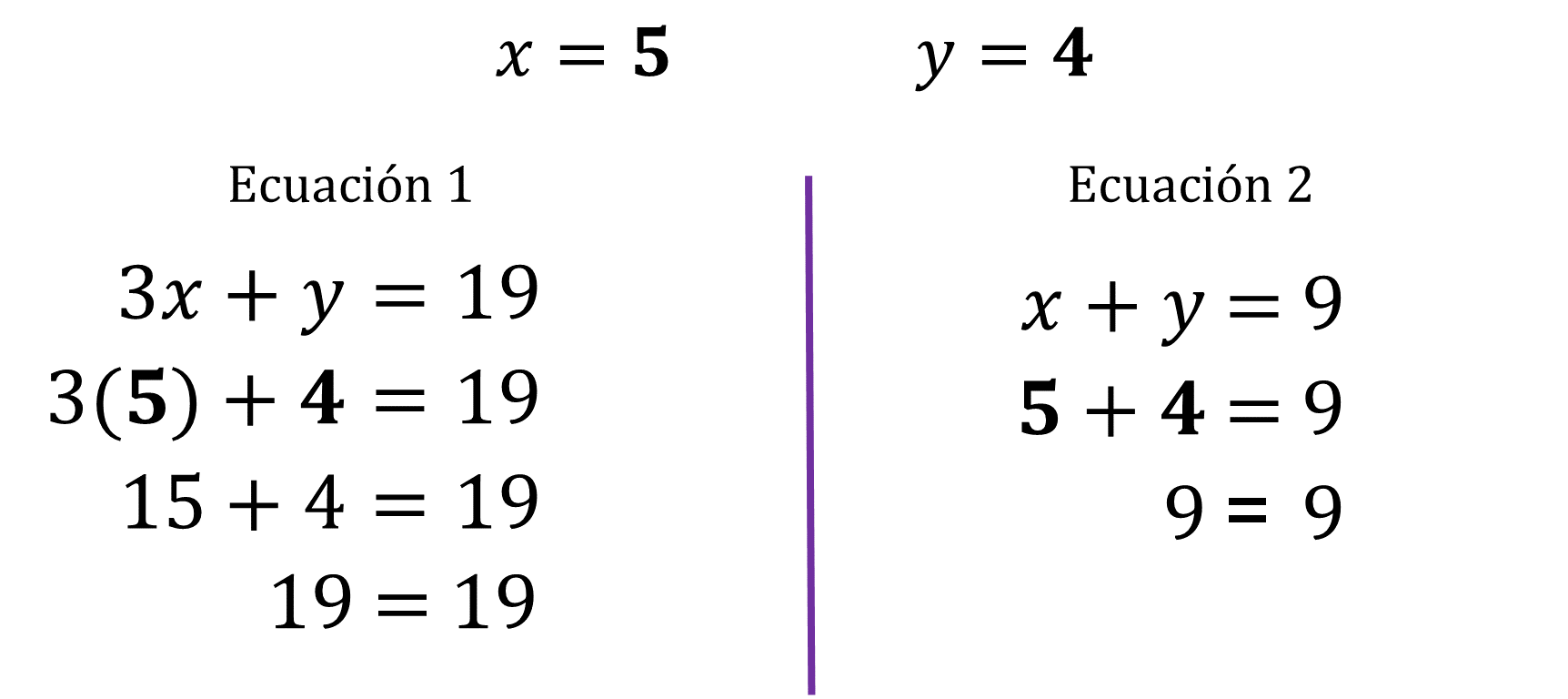
Al sustituir los valores de “x” y de “y”, se concluye que ambas ecuaciones son iguales, lo que te permite afirmar que, los valores encontrados hacen verdaderas las dos ecuaciones que integran el sistema.
Armando y Gabriela saben que el precio de los dulces que compraron es:

A continuación, resuelve la siguiente situación-problema, mediante el método algebraico más apropiado.
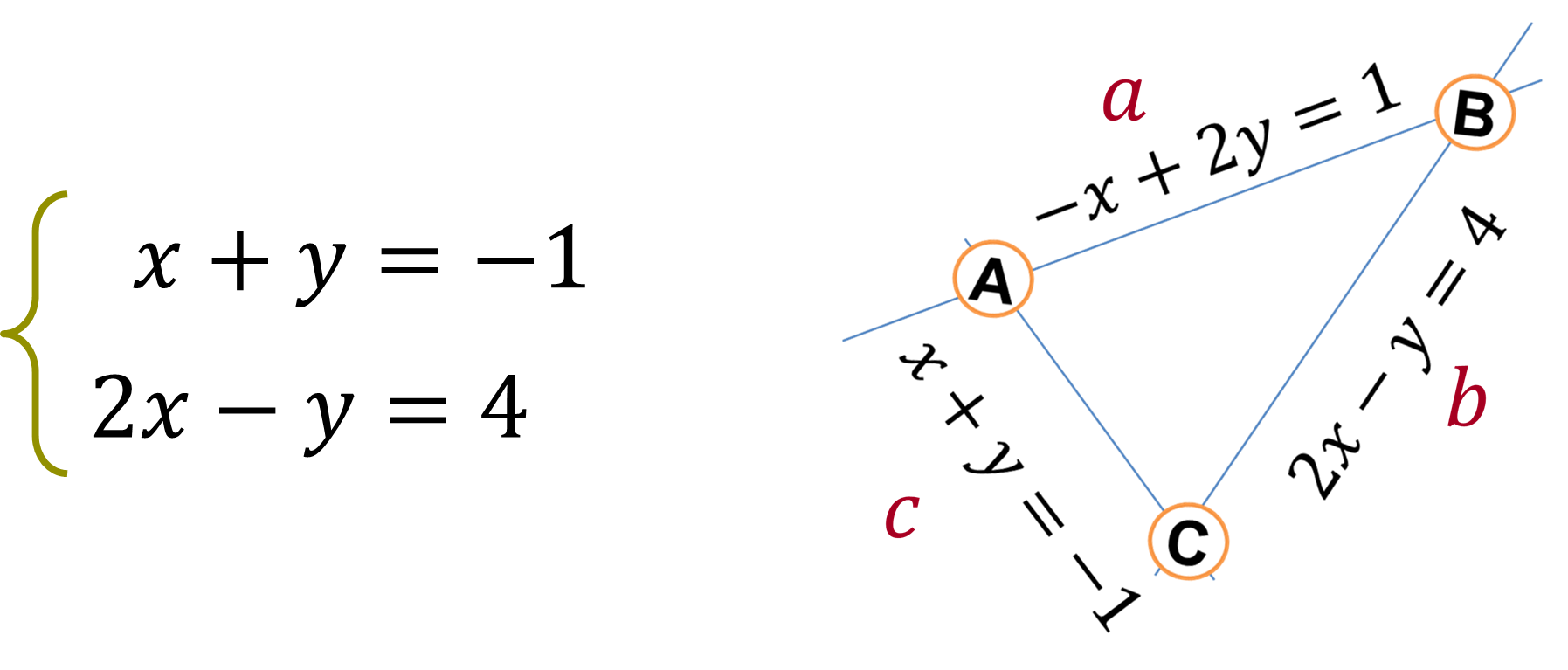
Situación-problema Triangulo
Un profesor les propuso a sus alumnos como reto resolver la siguiente situación-problema:
Los lados de un triángulo están delimitados por tres rectas, representadas por las siguientes ecuaciones
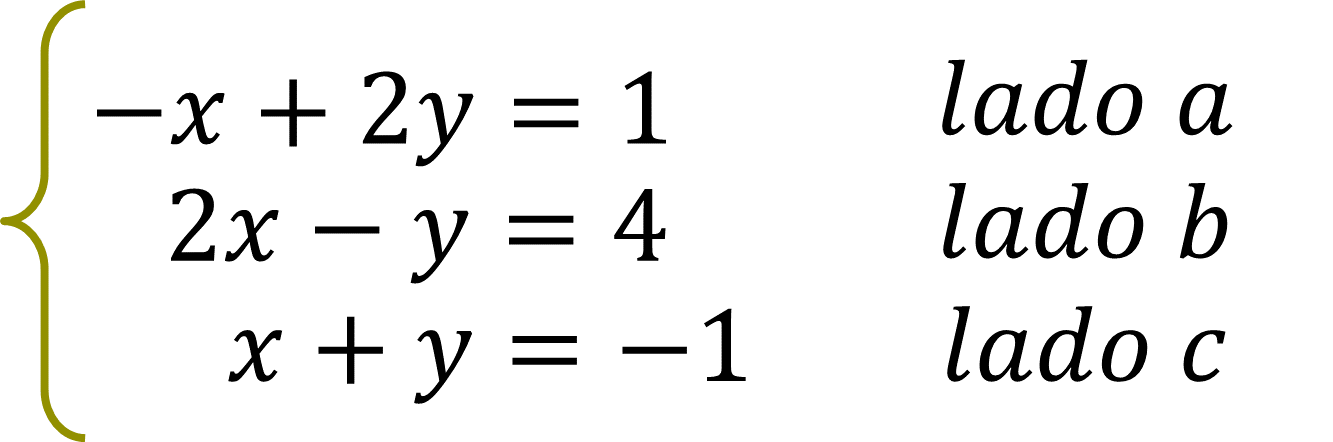
Determina:
¿Cuáles son las coordenadas de los vértices del triángulo?
Si se gráfica cada ecuación, ¿se formará el triángulo?
¿Qué método algebraico consideras apropiado para resolver el problema?
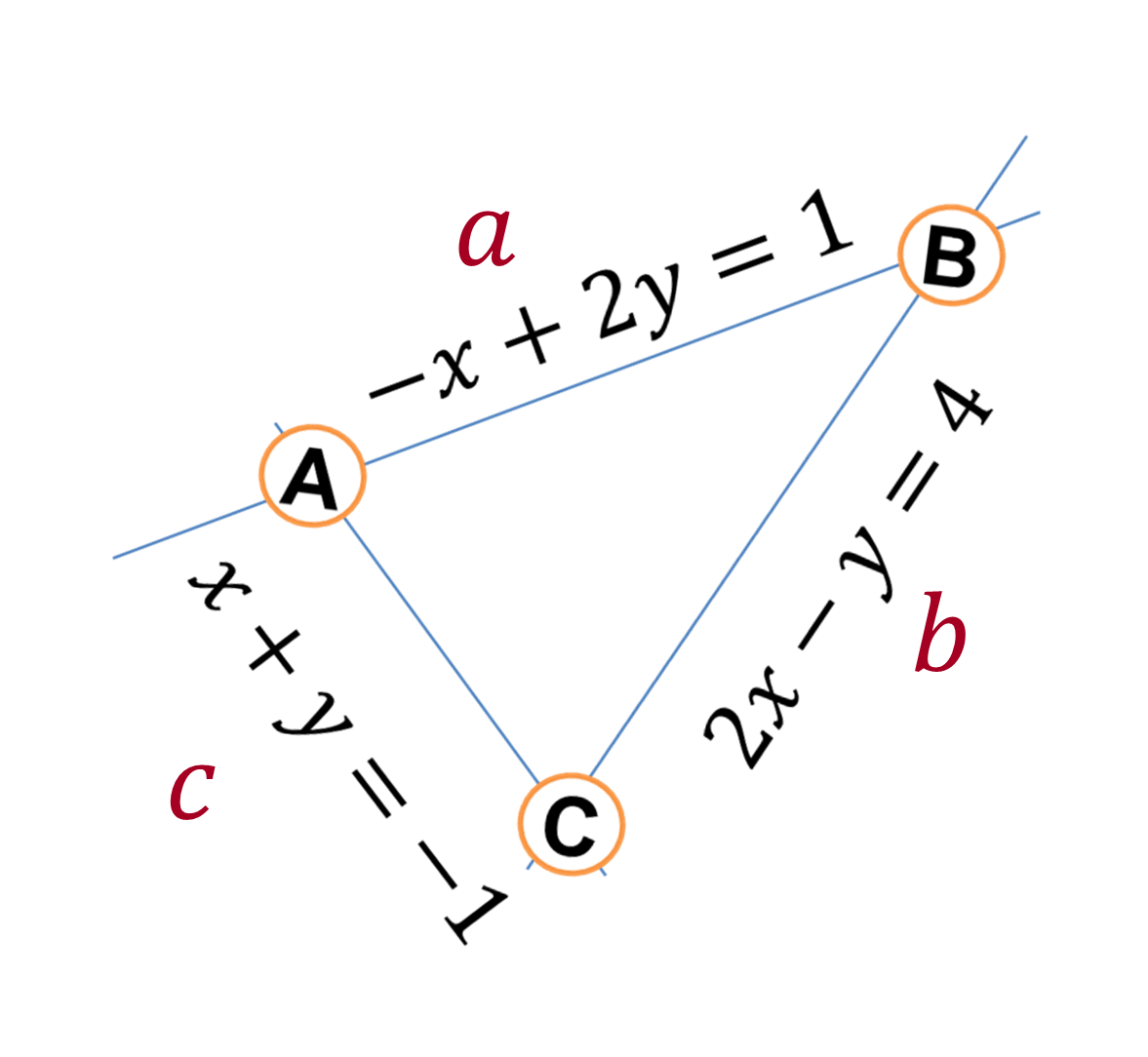
Puedes considerar que como las tres ecuaciones forman parte de un sistema que se relacionan entre sí, se dice que esta relación permite formar un triángulo.
Observa el triángulo y determina:
¿Qué lados del triángulo forman el sistema de ecuaciones lineales (2x2) para el cálculo de las coordenadas de los vértices de la figura?
Sistema de Ecuaciones
Las ecuaciones: -x + 2y = 1, x + y + = -1, forman el sistema A, para el cálculo de las coordenadas del vértice A.
Las ecuaciones: -x + 2y = 1, 2x – y = 4, forman el sistema B, para el cálculo de las coordenadas del vértice B.
Y las ecuaciones: x + y = -1, 2x – y = 4, forman el sistema C, para el cálculo de las coordenadas del vértice C.
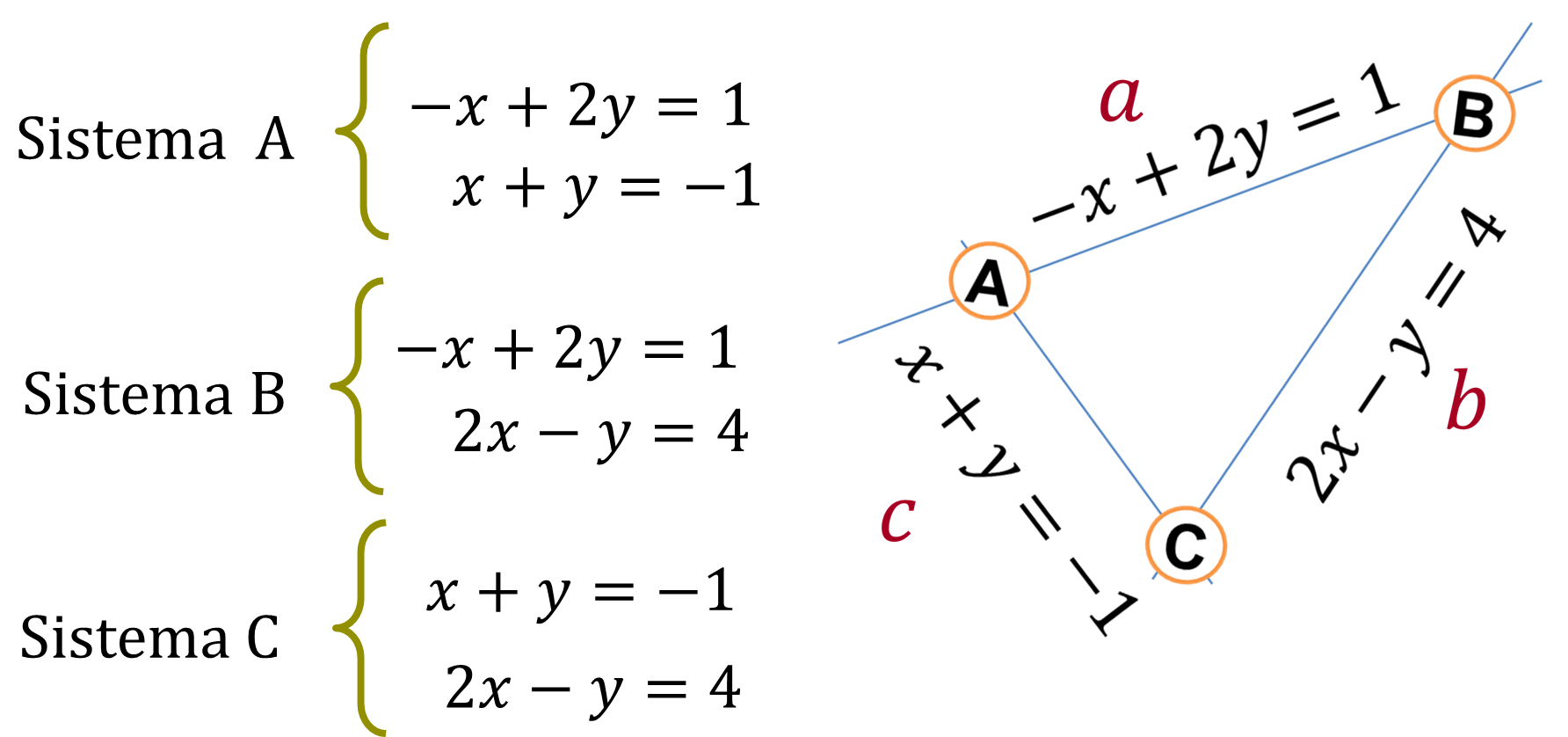
Ahora resuelve el sistema de ecuaciones para el vértice A.
¿Cuál de los métodos algebraicos consideras más apropiado para resolver?
Considerando que la situación-problema ya da como información las ecuaciones que forman tres sistemas, utiliza: El método algebraico de suma o resta, también conocido como método de eliminación.
¿Por qué?
Porque en el sistema formado tiene el mismo coeficiente en ambas ecuaciones, pero con diferente signo, de esta manera puedes eliminar la incógnita “x”, para tener una sola ecuación con una sola incógnita, es decir la incógnita “y”, y con ello después calcular los valores de “y” y de “x”.
Resolución del sistema de ecuaciones del Vértice A, método algebraico de suma y resta:
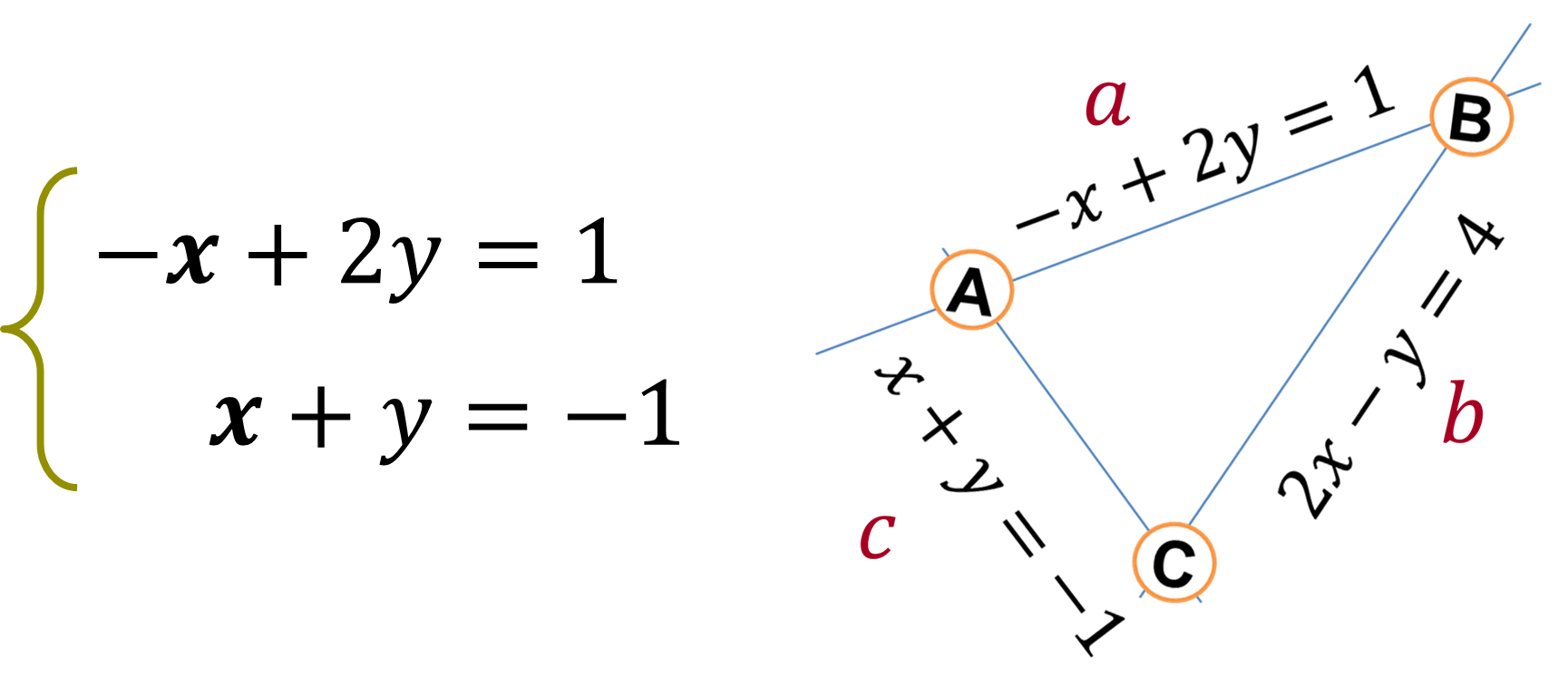
Partiendo del sistema de ecuaciones del vértice A procedemos a resolverlo mediante el método algebraico de suma y resta:
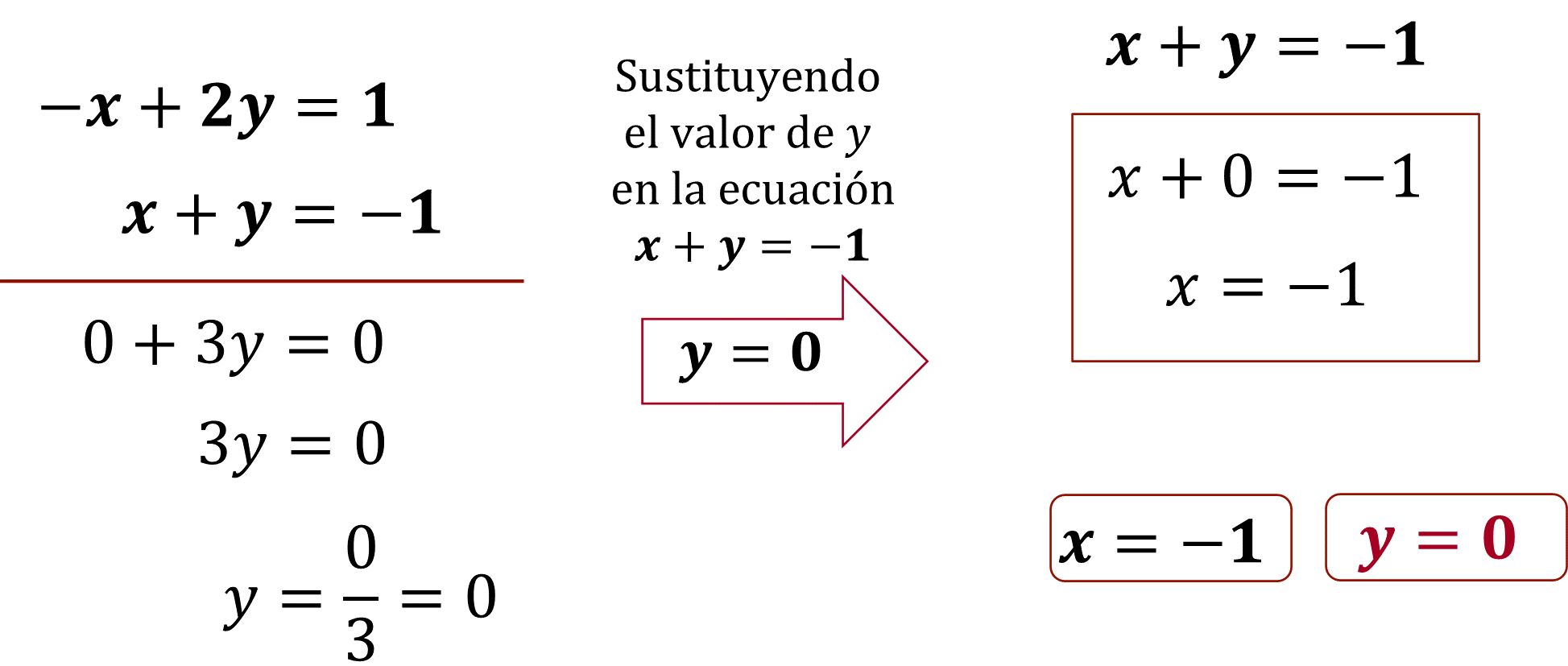
Por lo tanto, se obtiene que “y” es igual a cero. Y después de sustituir el valor de “y” en la segunda ecuación, queda que “x” es igual a uno negativo.
¿Qué significan los valores de “x y “y” en la situación del problema?
Las coordenadas del vértice A (-1,0)
Ahora resuelve el sistema de ecuaciones del vértice B.
¿Cuál de los métodos algebraicos consideras más apropiado para resolverlo?
Considerando que la situación-problema ya da como información las ecuaciones, utiliza: El método algebraico de sustitución.
¿Por qué?
Si observas la ecuación 1, -x + 2y = 1, el coeficiente de la incógnita “x” es un numeral uno, esta característica facilita despejar dicha incógnita, por lo que conviene utilizar el método de sustitución para resolver este sistema de ecuaciones lineales.
Resolución del sistema de ecuaciones del Vértice B, método algebraico de sustitución:
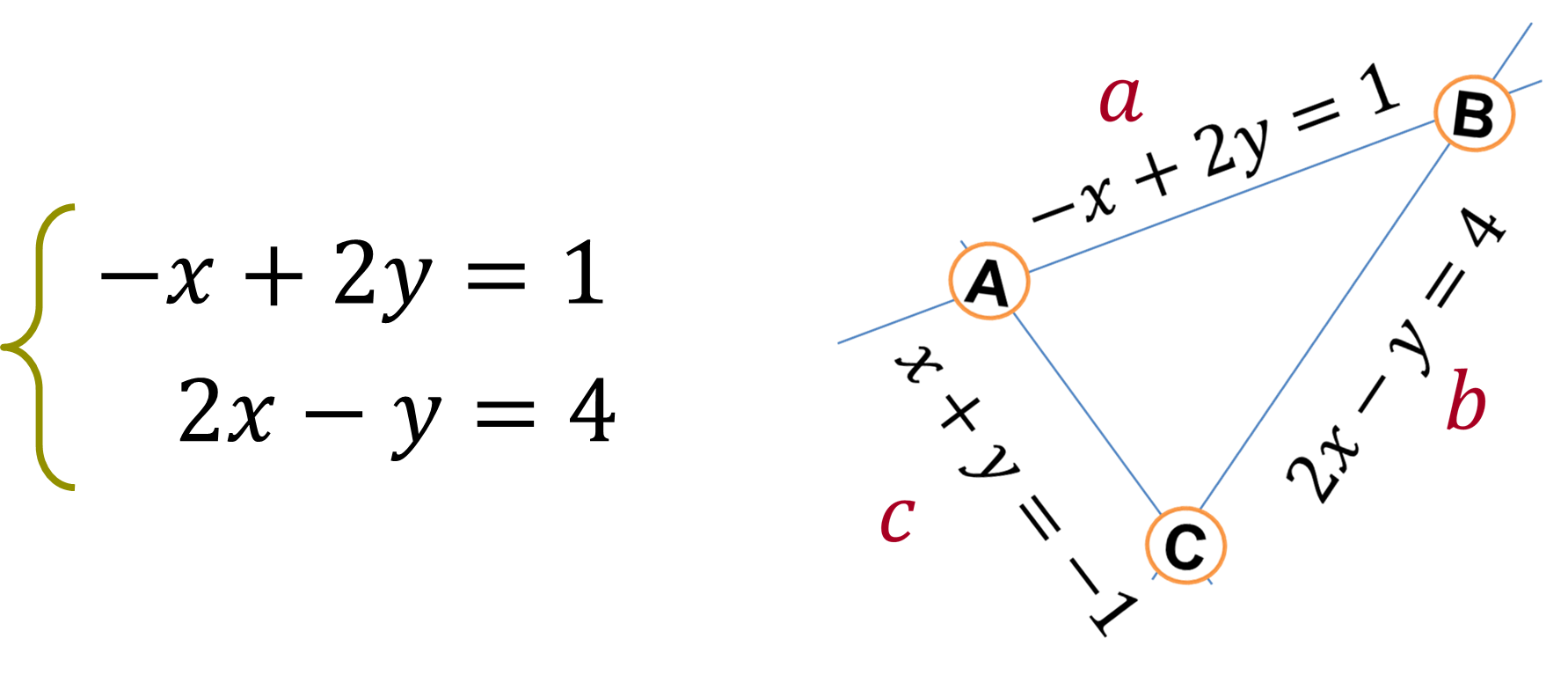
Partiendo del sistema de ecuaciones del vértice B, procede a resolverlo mediante el método algebraico de sustitución:

Se concluye que “y” es igual a 2.
Para encontrar el valor de “x” sustituye el valor numérico de “y” en la ecuación:
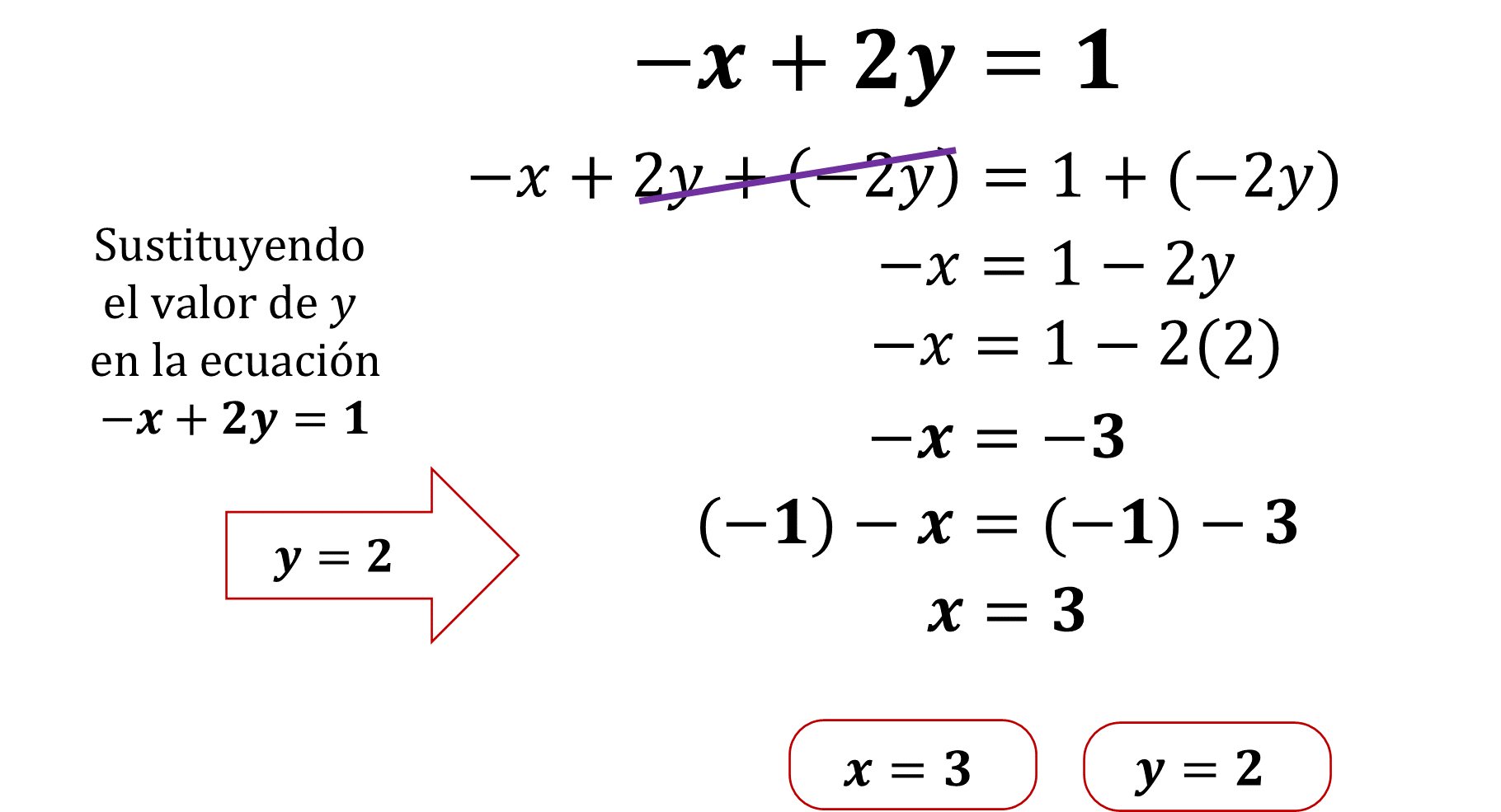
Se tiene que x = 3.
¿Qué significan los valores de “x y “y” en la situación del problema?
Las coordenadas del vértice B (3,2)
Ahora resuelve el sistema de ecuaciones para el vértice C.
¿Cuál de los métodos algebraicos consideran ustedes más apropiado para resolverlo?
El método algebraico de suma o resta, también conocido como método de eliminación.
¿Por qué?
Porque la incógnita “y” es igual en ambas ecuaciones y con diferente signo, de esta manera puedes eliminar la incógnita “y”, para tener una ecuación con una incógnita y así calcular los valores de “x” y “y”.
Resolución del sistema de ecuaciones del Vértice C, método algebraico de suma y resta:
Partiendo del sistema de ecuaciones del vértice C procede a resolverlo mediante el método algebraico de suma y resta:

El resultado obtenido es: x = 1, y = -2
¿Qué significan los valores de “x” y “y” en la situación del problema?
Las coordenadas del vértice C (1,-2)
Recuerda las preguntas planteadas en la situación-problema:
¿Cuáles son las coordenadas de los vértices de la figura?
¿Qué método algebraico consideras el apropiado para resolver la situación-problema?
Es importante observar las características de cada sistema de ecuaciones lineales para decidir cuál método es más conveniente utilizar en cada caso.
Solución del problema:

En esta situación, para el vértice A, las coordenadas (x, y) son (-1,0) y se resolvió mediante el método algebraico de suma y resta.
Para el vértice B, las coordenadas (x, y) son (3,2) y se resolvió mediante el método algebraico por sustitución.
Para el vértice C, las coordenadas (x, y) son (1,-2) y se resolvió mediante el método algebraico de suma y resta.
Puedes formar el triángulo ABC al unir los puntos coordenados A, B y C mediante líneas rectas, las cuales representan la relación del sistema de ecuaciones lineales (2x2), así como los puntos de intersección que forman los vértices de la figura.
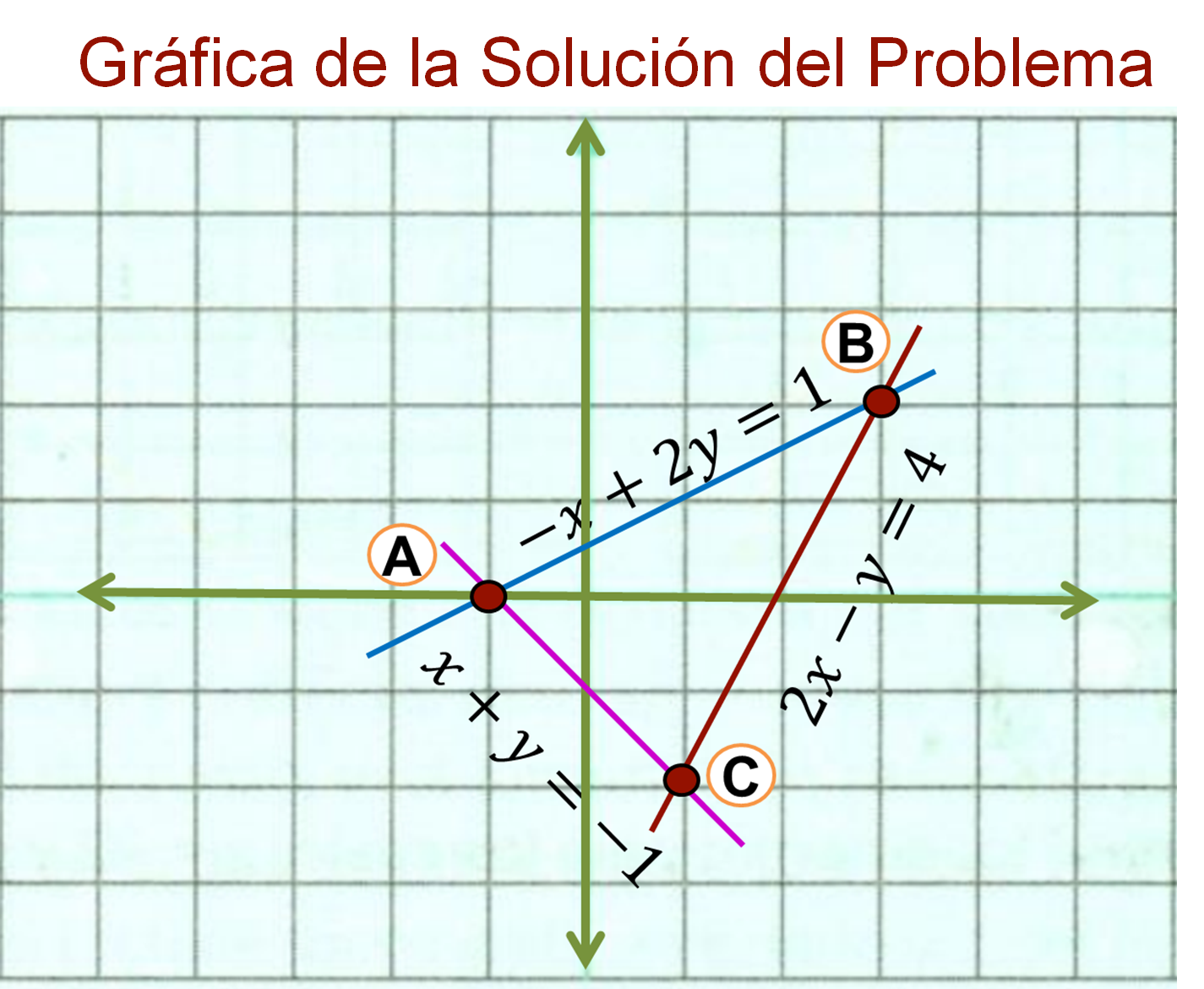
Recuerda que, al haber intersección entre rectas, estas ante un sistema de ecuaciones lineales con solución.
En esta ocasión aprendiste que un sistema de ecuaciones lineales 2x2 puede resolverse utilizando alguno de los diferentes métodos, siempre y cuando los utilices de manera apropiada, esto te permitirá llegar a la respuesta correcta.
También, si prestas atención detenidamente a la forma de las ecuaciones que integran el sistema, puedes elegir un método de resolución que sea más conveniente, de acuerdo con las características que presenta cada ecuación.
Sin importar el método de resolución utilizado, es indispensable comprobar que los valores numéricos encontrados de las literales que eran las dos incógnitas “x” y “y”, las cuales hacen verdaderas las dos ecuaciones.
El Reto de Hoy:
Revisa y practica lo aprendido. Usa tu libro de texto de Matemáticas de segundo grado, buscando el tema que se abordó en la sesión.
Finalmente, contesta la siguiente pregunta:
¿Descubriste algo nuevo al utilizar cada uno de los cuatro métodos para resolver un mismo sistema de ecuaciones lineales 2x2?


No hay comentarios.:
Publicar un comentario