SEGUNDOS AÑOS 20/10/2020 Equivalencia de expresiones algebraicas de una sucesión

 

SEGUNDOS AÑOS 

20/10/2020

Equivalencia de expresiones algebraicas de una sucesión

Aprendizaje esperado: Verifica algebraicamente la equivalencia de expresiones de primer grado, formuladas a partir de sucesiones.

 

Énfasis: Verificar la equivalencia de expresiones algebraicas que representen la regla de una misma sucesión.

 

 

¿Qué vamos a aprender?

 

En la sesión anterior conociste cómo encontrar la regla general de una sucesión, ya sea de figuras o de números. Ahora, analizarás que hay distintas maneras de expresar algebraicamente la regla de una misma sucesión, y que todas ellas son equivalentes.

 

 

¿Qué hacemos?

 

Observa la siguiente situación y comprueba la equivalencia de expresiones algebraicas que representen la regla de una misma sucesión.

 

Situación 1

 

En un parque ecológico se planea la construcción de estanques de diversos tamaños, y pueden ser tantos como lo permita la extensión del terreno en donde se colocarán, pero se debe seguir el mismo patrón de los tres primeros. Observa el borde de los primeros tres estanques, estará formado por losetas cuadradas, como se muestra en la figura.

 

 

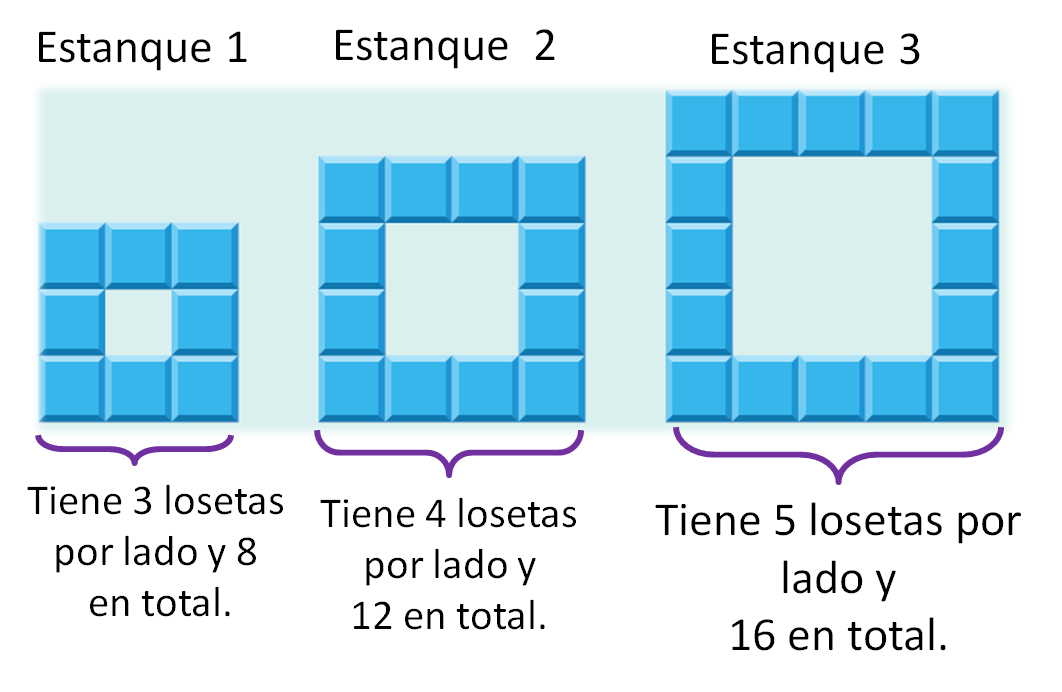
Los tres estanques tienen forma cuadrangular:

 

• El estanque 1 tiene 3 losetas por lado y 8 losetas en total.
• El estanque 2 tiene 4 losetas por lado y 12 losetas en total.
• El estanque 3 tiene 5 losetas por lado y 16 losetas en total.

 

Si se considera que se colocarán más de tres estanques, y se asocia a cada estanque el número de losetas por lado y el número de losetas en total, al modelar matemáticamente la situación se tiene que:

 

 

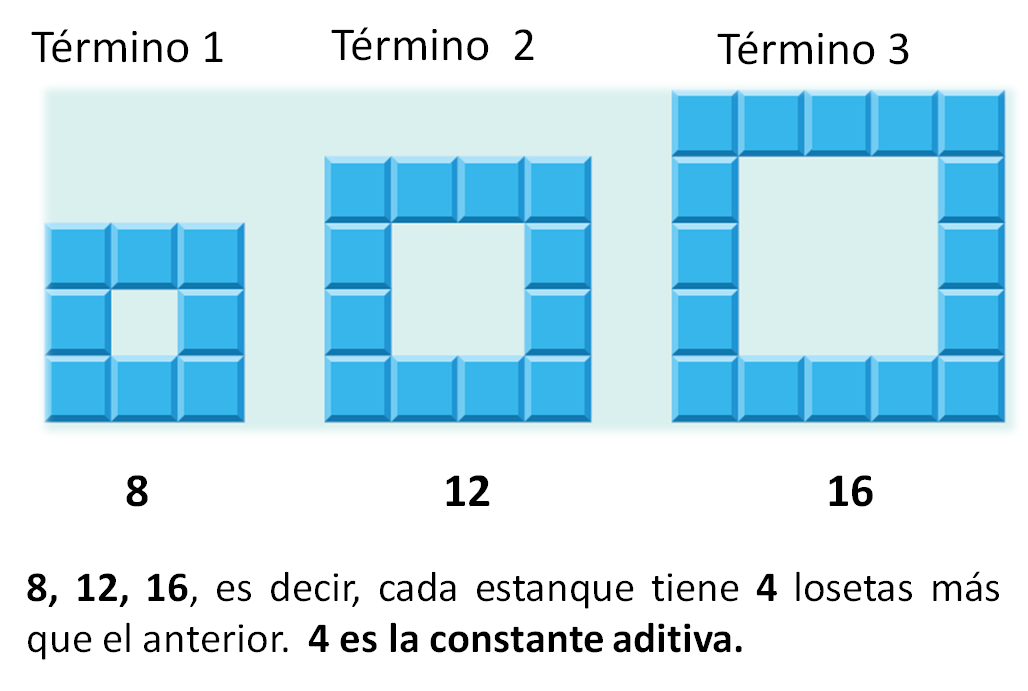
• El término 1 tiene 3 losetas por lado y 8 losetas en total.
• El término 2 tiene 4 losetas por lado y 12 losetas en total.
• Y el término 3 tiene 5 losetas por lado y 16 losetas en total.

 

De esta manera, se tiene que el número total de losetas que integra cada estanque se representa con la siguiente sucesión:

 

8, 12, 16

 

Es decir, el siguiente estanque tiene 4 losetas más que el anterior. “4” es la constante aditiva en esta sucesión y ayuda a saber que:

 

• Del primero al segundo término hay 4 losetas más: 8 + 4 = 12
• Del segundo término al tercero hay 4 losetas más: 12 + 4 = 16, y así sucesivamente.
• La constante aditiva también indica la diferencia entre un término y otro, por ejemplo, la diferencia del número de losetas del término 2 y 1 es 4: 12 – 8 = 4.
• Si se continua la sucesión que representa el número de losetas totales en el siguiente estanque, se tiene:

 

8, 12, 16, 20, 24…

 

En la sucesión anterior se resaltó el cuarto término, que es 20; esto se interpreta como: el estanque 4 tiene un total de 20 losetas, es decir, 4 losetas más que el estanque 3: 16 + 4 = 20. O que la diferencia del total de losetas entre estos estanques es: 20 – 16 = 4

 

Continua con el análisis: ¿cuántas losetas tiene en total el estanque que tiene 8 losetas por lado? 

 

 

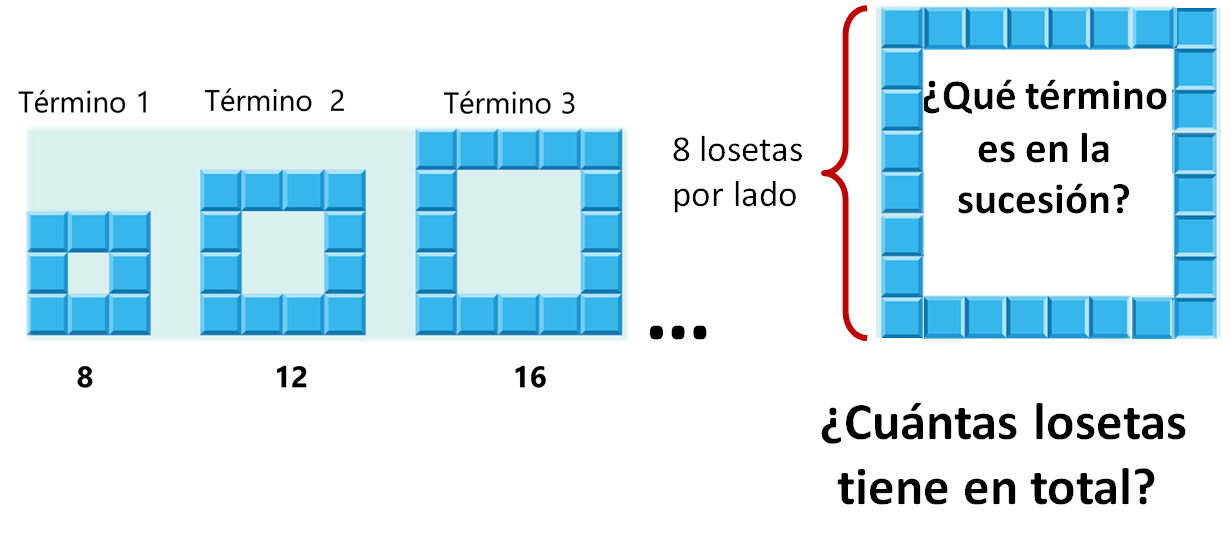
Analiza cada caso para obtener la respuesta.

El término 1 tiene 8 losetas en total; el término 2, 12 losetas; el término 3, 16 losetas, pero no se sabe cuál es el término de la sucesión que ocupa el estanque con 8 losetas por lado.

 

El registro tabular o tabla de datos es útil para organizar y comparar información numérica, por lo que, en esta ocasión, recurrirás a ella.

 

Registra en la columna el número del término de la sucesión y lo relacionas con el total de losetas por lado de los estanques.

 

 

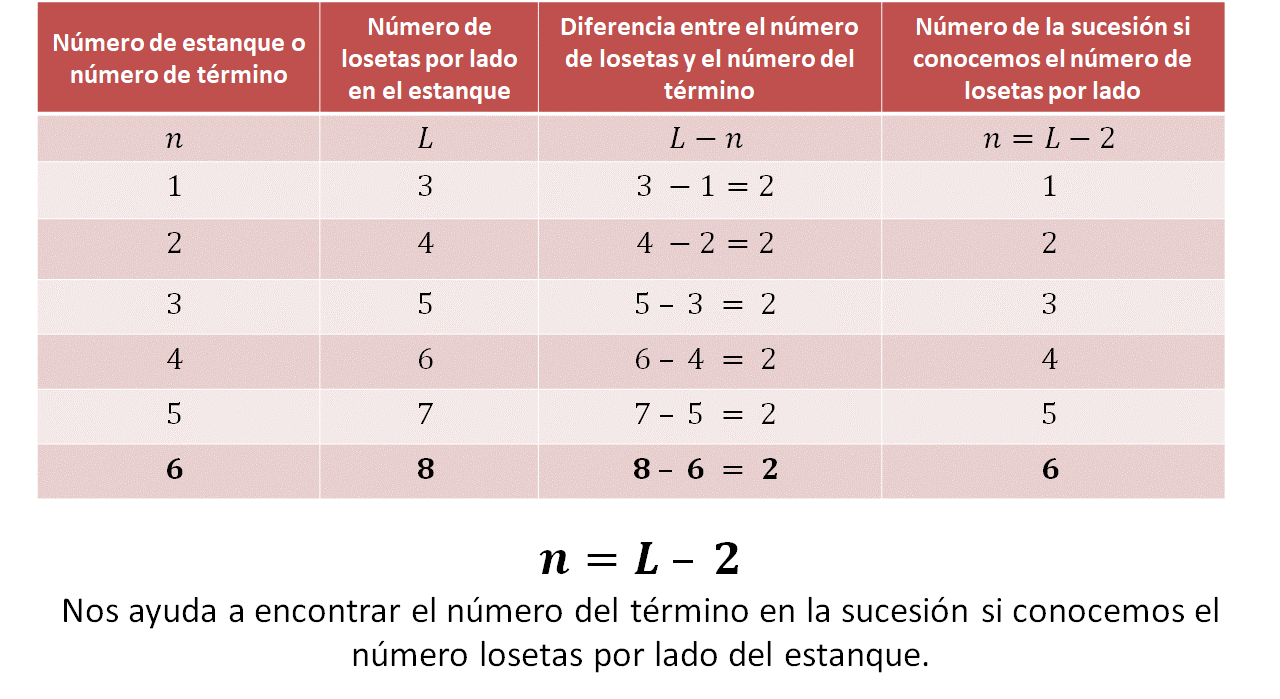
El estanque 1 corresponde al término 1 de la sucesión y tiene 3 losetas por lado.

El término 2 de la sucesión tiene 4 losetas por lado, el término 3 de la sucesión tiene 5 losetas por lado, y así sucesivamente hasta saber que el término 6 tiene 8 losetas por lado.

La tabla de datos te ha ayudado a saber el término que ocupa en la sucesión el estanque con 8 losetas por lado, pero ¿qué término en la sucesión ocupa el estanque que tiene 80 o 90 losetas por lado? Hacerlo en la tabla de datos sería poco práctico. Por ello, te ves en la necesidad de generalizar, es decir, encontrar una expresión que te ayude a determinar el número de término al que le corresponde un cierto número de losetas por lado que tiene ese estanque.

La tabla te ha sido útil también para identificar que la diferencia entre el total de losetas por lado y el término es de 2, y si “n” representa el término de la sucesión y “L” representa el número de losetas por lado, se tiene que la expresión n = L - 2 te ayudará a encontrar cualquier término en la sucesión.

Prueba con L = 8, es decir, con el estanque que tiene 8 losetas por lado: 8 – 2 = 6, el estanque con 8 losetas por lado es el término 6 de la sucesión.

Ahora, ¿cuál es la expresión algebraica que permite conocer el total de losetas que tiene el estanque con 8 losetas por lado?

Si se llama “n” a cualquier término de la sucesión, y sabes que para obtener el siguiente término se suma 4 al valor del término anterior, se puede establecer la expresión: “n” por cuatro más cuatro, (n4+4), que, reacomodándola, de ahora en adelante la se llamará cuatro “n” más cuatro (4n + 4).

 

Al sustituir la expresión 4n + 4, puedes saber el total de losetas que tiene cada estanque, en armonía con el término que ocupan en la sucesión. Observa la siguiente tabla de datos:

 

 

Por ejemplo, el término 6 tiene 8 losetas por lado, y 28 losetas en total, ya que 6(4) + 4 = 24 + 4 = 28

 

También puedes utilizar otra expresión algebraica que modela la sucesión de manera correcta: 4(n+1) 

 

Analiza: en la expresión 4(n+1) “n” representa el término de la sucesión, entonces realiza la sustitución con los valores numéricos de la tabla de datos.

 

Aplica la jerarquía de las operaciones para resolver la sustitución en la columna 3. Observa la siguiente tabla con ambas expresiones:

 

4n + 4

4 (n+1)

 

 

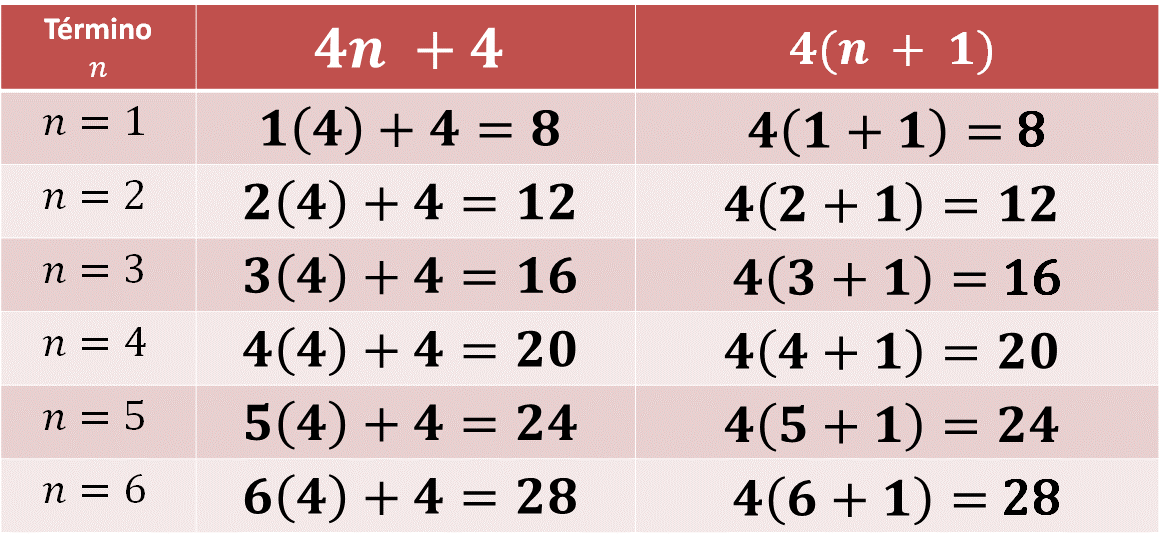
En la fila 1 se tiene que: 1+1 = 2; 4(2) = 8 El resultado en ambas columnas es el mismo.

 

En la fila 2 se tiene que: 2+1 = 3; 4(3) = 12 El resultado en ambas columnas es el mismo.

 

Puedes continuar y te darás cuenta de que con ambas expresiones algebraicas puedes obtener los mismos resultados.

 

Ahora verifica ambas expresiones algebraicas con datos que no tengas en la tabla.

 

¿Cuál es el total de losetas de un estanque que en la sucesión ocupa el término 12?

 

Dada la expresión algebraica: 

 

 

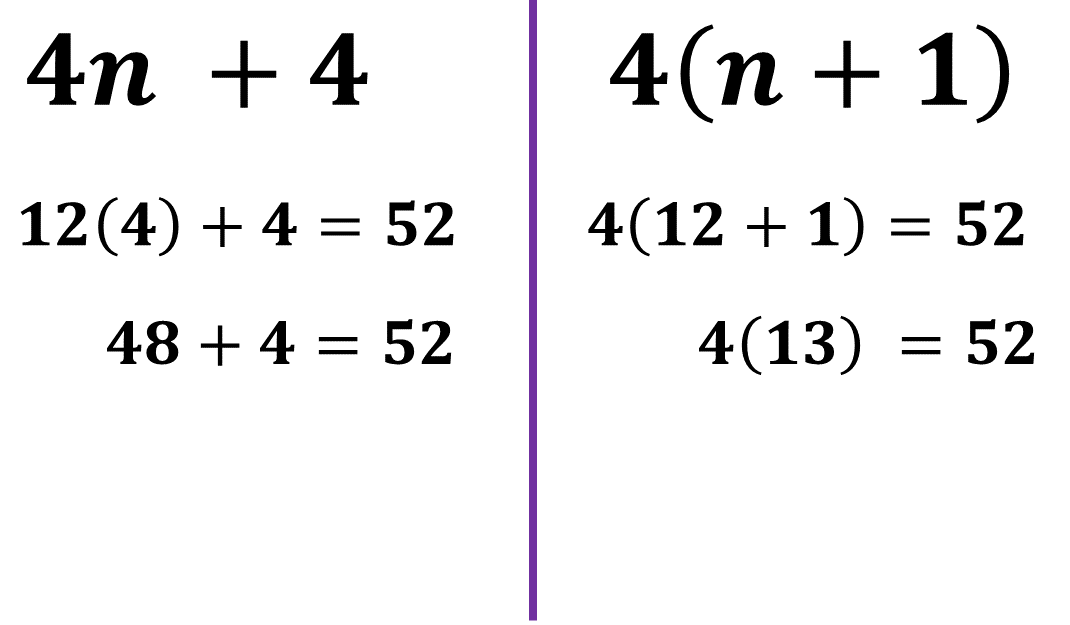
Ambos resultados son iguales.

 

De acuerdo con los casos particulares, se puede afirmar que las expresiones algebraicas son equivalentes. 

 

Es decir, se representan matemáticamente de forma diferente, pero al aplicarlas, los resultados son los mismos.

 

 

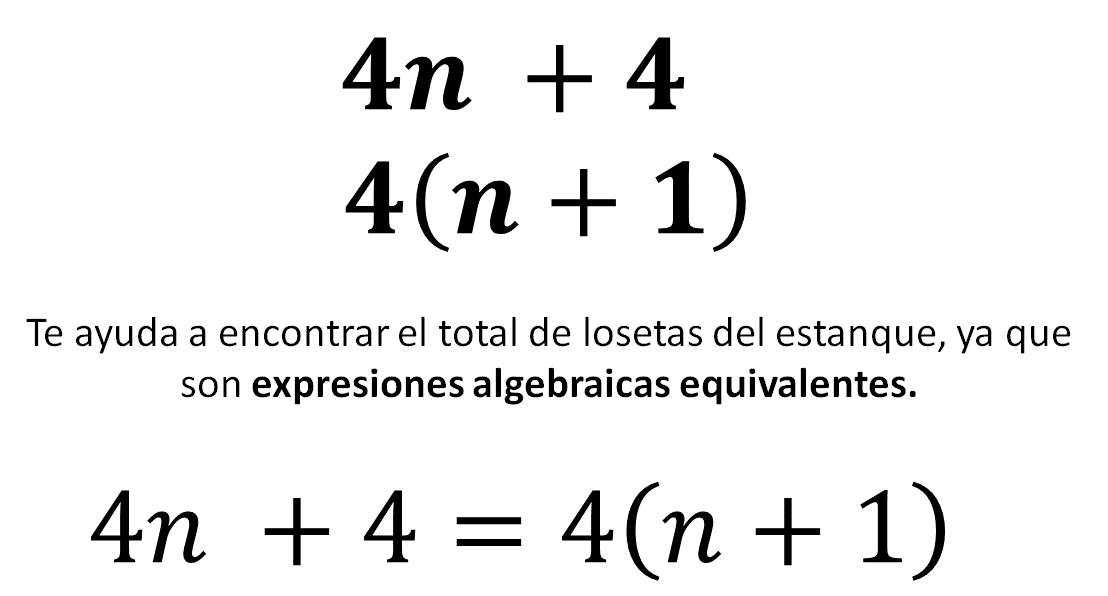
Has aprendido que una sucesión puede tener al menos dos expresiones algebraicas que las modelen correctamente, y que dichas expresiones algebraicas son equivalentes.

 

A continuación, analiza otra situación para profundizar en el tema de estudio.

Lía y Raquel están jugando a identificar las expresiones algebraicas que representan sucesiones.

Por turnos se muestran tarjetas con sucesiones numéricas y una expresión algebraica que las representa para que la jugadora contraria describa con palabras la regla general y una expresión algebraica equivalente a la que está en la tarjeta.

Observa el primer caso: Raquel muestra su tarjeta.

 

 

¿Qué otra expresión algebraica propones que sea equivalente a: 3+2(n-1)?

Ahora, observa que contesto Lía.

La expresión algebraica equivalente que considero correcta es:

 

¿Cómo puedes verificar si las expresiones algebraicas propuestas corresponden a la sucesión dada?

Utiliza una tabla para verificar si las expresiones algebraicas propuestas por Raquel y Lía modelan la regla general de la sucesión dada.

Al sustituir los valores numéricos en las expresiones algebraicas, se tiene que “n” corresponde al término de la sucesión. Observa cómo quedo la tabla con ambas expresiones algebraicas:

 

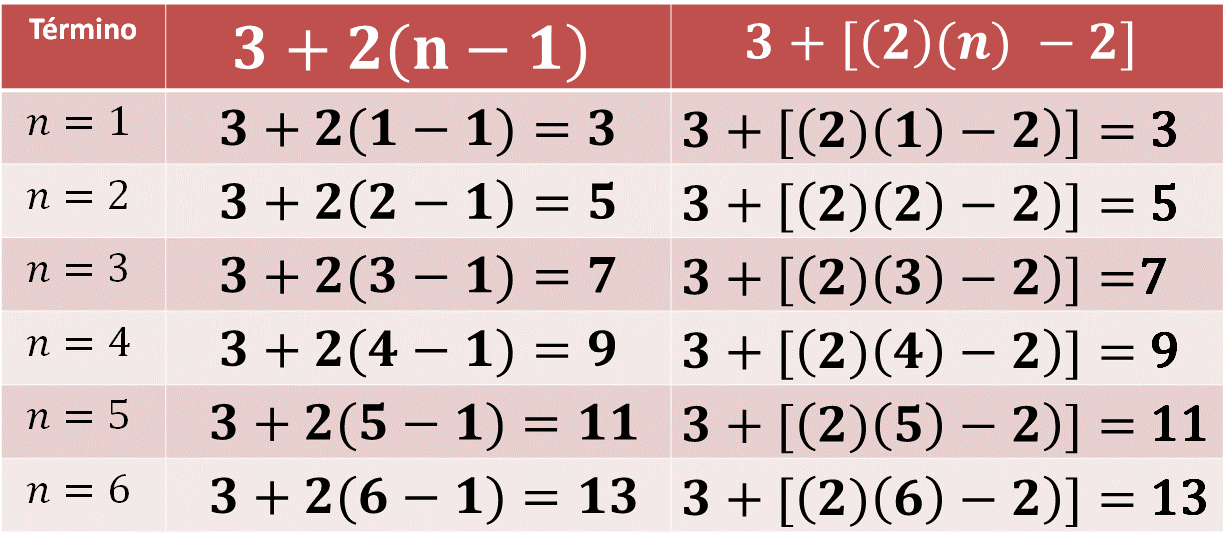
Presta atención cuando “n” es igual a uno:

 

• En la expresión: 3+2 (n-1) al sustituir “n” por el valor de 1 queda 3+2 (1-1) esto es, igual a 3
• Ahora, en la expresión: 3 + [(2)(n)-2]   observa que al sustituir “n” por el valor de 1 queda 3 + [(2)(1)-2] esto es, igual a tres.

 

Como puedes darte cuenta, al sustituir el valor numérico de “n”, en este caso, “n” igual con “1” en ambas expresiones algebraicas, se obtiene el mismo resultado: 3

Observa qué pasa cuando “n” es igual a dos:

• 3+2 (2-1); al realizar las operaciones el resultado es cinco. Por otra parte, 3 + [(2)(2)-2]; al realizar las operaciones, el resultado es cinco.

Con ambas expresiones algebraicas se tiene el mismo resultado: 5

Y así sucesivamente como se muestra en la tabla anterior. Con ambas expresiones algebraicas se tiene el mismo resultado, por lo que se puede concluir que ambas expresiones algebraicas modelan correctamente la sucesión A.

 

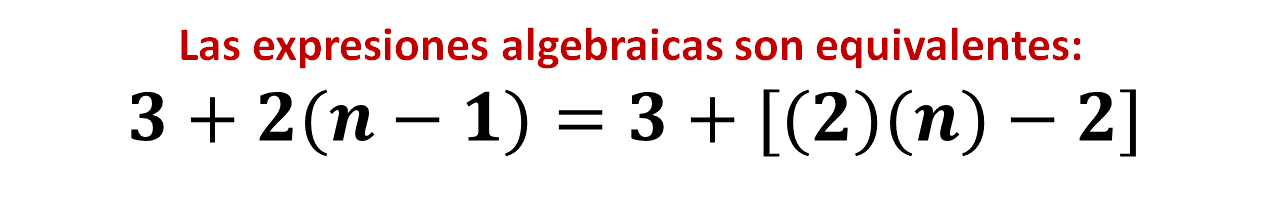
Con lo que has analizado hasta ahora:

¿Sólo una regla general puede representar una sucesión?, ¿cuál es tu respuesta?

Anótala en tu cuaderno para contrastar tu argumento más adelante. 

Ahora es el turno de Lía, quien plantea lo siguiente:

 

 

Raquel responde lo siguiente:

 

 

Utiliza una tabla para comprobar si las reglas de las sucesiones que propusieron Lía y Raquel las representan correctamente. Al sustituir los valores numéricos en las expresiones algebraicas, tienes que “n” corresponde al término de la sucesión. Observa cómo quedo la tabla con ambas expresiones algebraicas:

 

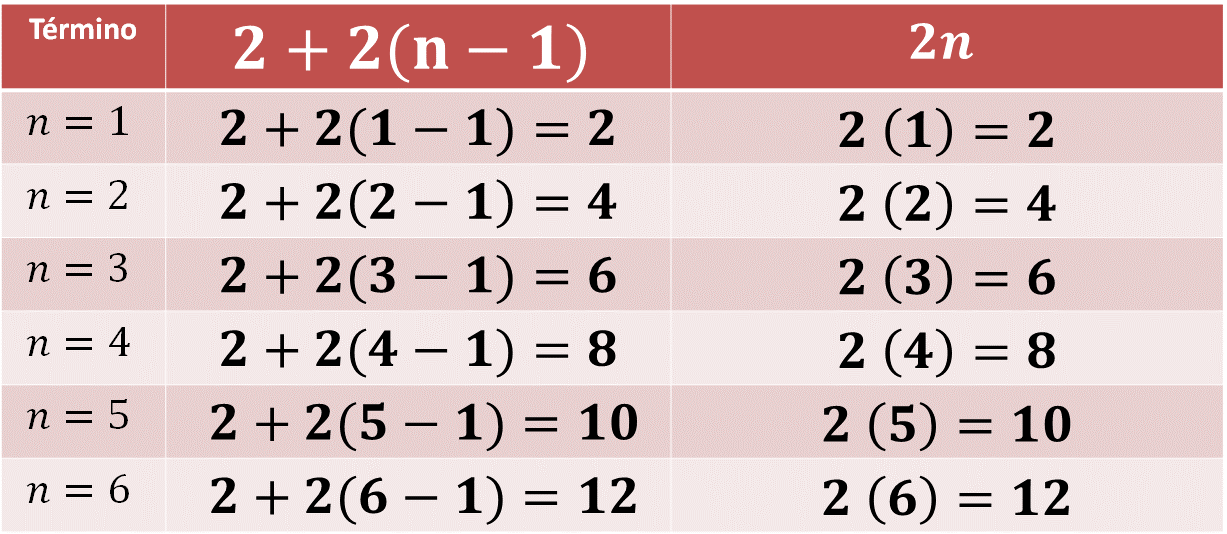
Observa cuando “n” es igual a uno:

En la expresión:

2 + 2 (n-1)  al sustituir “n” por el valor de “1”  queda: 2 + 2 (1-1) esto es igual a 2

Ahora, en la expresión:

2n al sustituir “n” por el valor de “1” queda: 2(1) igual a dos.

Como puedes darte cuenta, al sustituir el valor numérico de “n”, en este caso, “n” igual con “1” en ambas expresiones algebraicas se obtiene el mismo resultado: 2

Observa qué pasa cuando “n” es igual a dos:

2 + 2 (2-1); al realizar las operaciones, el resultado es cuatro. Por otra parte, 2(2); al realizar el producto, el resultado es cuatro.

Con ambas expresiones algebraicas se obtiene el mismo resultado: cuatro.

Como se muestra en la tabla, lo mismo sucede cuando “n” es igual a 3, 4, 5 y 6, con ambas expresiones algebraicas se obtiene el mismo resultado.

Por lo que se puede concluir que ambas expresiones algebraicas que modelan la sucesión B son equivalentes.

Has aprendido sobre la equivalencia entre dos expresiones algebraicas que modelan una misma sucesión. Y has usado el registro tabular como medio para comparar y verificar su equivalencia.

A continuación, analiza la siguiente sucesión y determina si las reglas generales que se encuentran debajo de ella pertenecen a la sucesión.

Escribe las que consideras que representan la sucesión y, si ninguna de ellas la representa, escribe la expresión.

 

 

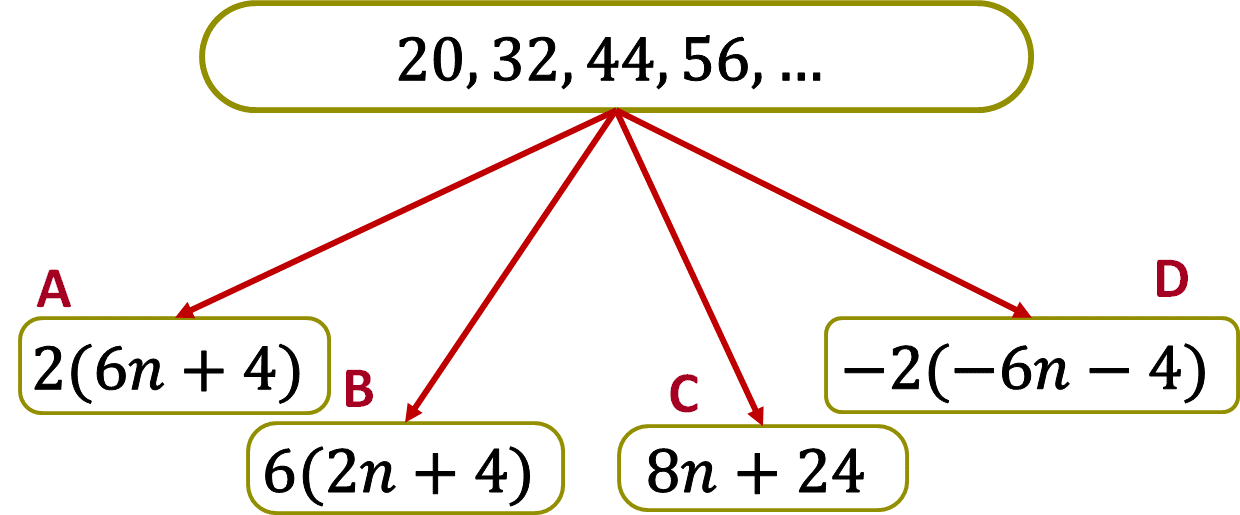
¿Cuál o cuáles son las expresiones algebraicas que la modelan?

En la sucesión de 20, 32, 44, 56…, tienes cuatro reglas.

Determina los cuatro primeros números de cada una de las reglas para saber si pertenecen a la sucesión.

En la regla A: dos que multiplica el binomio de seis “n” más cuatro.

 

 

Al sustituir los primeros cuatro valores del término “n” en la regla, se puede observar que sí corresponden a la sucesión, 20, 32, 44, 56…

Ahora, observa qué sucede si se sustituyen los valores del término “n” (1, 2, 3 y 4) en la regla general o expresión algebraica: 6(2n + 4)

 

 

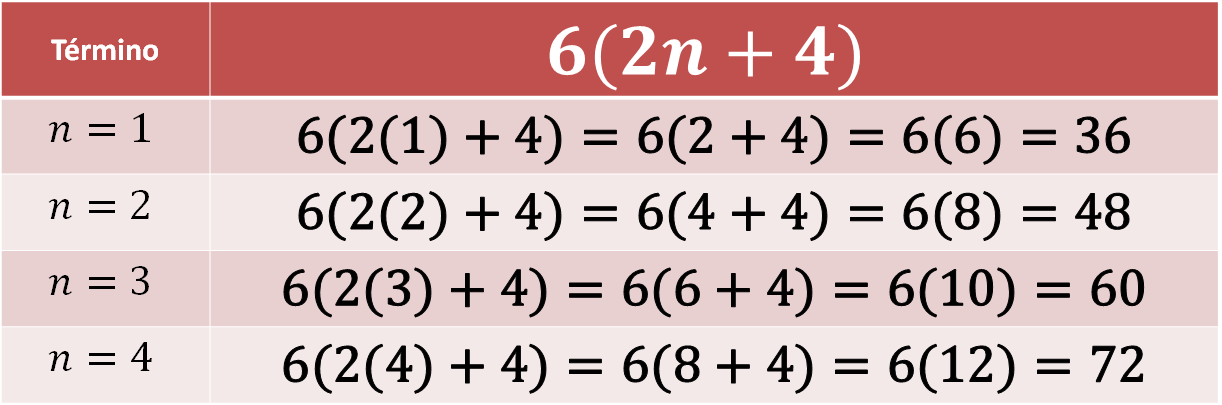
Los resultados de esta sucesión no corresponden a la sucesión dada porque se obtuvieron los siguientes resultados: 36, 48, 60, 72…

Observa qué sucede con la tercera regla general o expresión algebraica.

 

 

La sucesión de esta regla es:

32, 40, 48, 56… por lo que los resultados no corresponden a la sucesión propuesta.

Ahora comprueba la última regla dada.

 

 

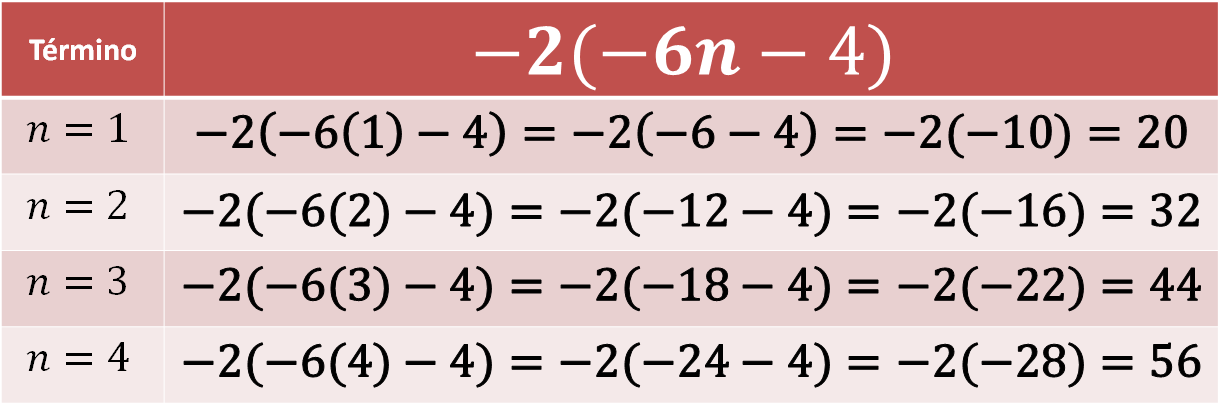
Al sustituir los primeros términos en la regla, se puede observar que los resultados sí corresponden a la sucesión dada:

 

20, 32, 44, 56…

 

Dada la sucesión:

 

 

Las expresiones algebraicas equivalentes son:

 

 

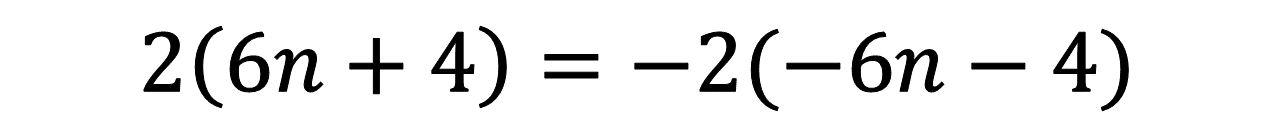
En esta lección has aprendido que cuando dos o más expresiones algebraicas corresponden a la regla general de una misma sucesión, entonces son equivalentes.

Recuerda revisar y practicar lo aprendido, puedes apoyarte de tu libro de texto de Matemáticas de segundo grado, buscando el tema que estudiaste en la lección.

 

 

El Reto de Hoy:

 

Es hora de aplicar lo aprendido. Analiza la siguiente sucesión y subraya las expresiones algebraicas que representen la regla general para la sucesión. Después, verifica su equivalencia algebraica.

 

 

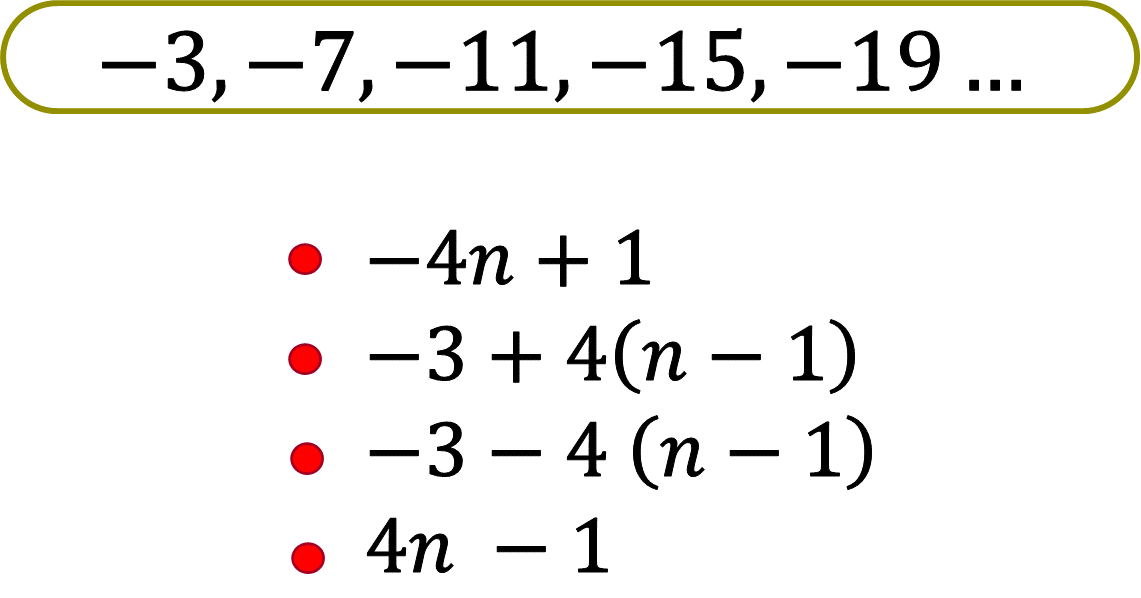
Finalmente, realiza la siguiente reflexión:

¿Habrá otra forma de determinar que estas dos expresiones son equivalentes?

¿Qué sucedería si se realiza el producto de la constante por el binomio en cada expresión?