SEGUNDOS AÑOS
FECHA:09/10/2020
TEMA: Resolución de problemas mediante un sistema de ecuaciones lineales con el método de igualación II
Aprendizaje esperado: Resuelve problemas mediante la formulación y solución algebraica de sistemas de dos ecuaciones lineales con dos incógnitas.
Énfasis: Resolver problemas mediante el planteamiento y resolución de sistemas de ecuaciones lineales con dos incógnitas utilizando el método de igualación.
¿Qué vamos a aprender?
Continuarás con el estudio de la resolución de problemas mediante un sistema de ecuaciones lineales con dos incógnitas. Ahora utilizando el método de igualación II, y como se trata de un método, todo método implica un orden.
Se enfatiza la importancia de que en Matemáticas evites memorizar cada paso, es mejor que comprendas en qué consiste cada uno de los pasos del método de igualación, y una vez que lo comprendas, utilizarlo en la resolución de problemas algebraicos.
¿Qué hacemos?
Retoma el ejercicio que se propuso la sesión pasada y observa la resolución del problema mediante el sistema de ecuaciones lineales 2x2, utilizando el método de igualación; cuyo propósito es comprender, dar sentido y significado a los pasos del método de igualación para la resolución de diversas situaciones.
Ejercicio 1
En un partido de básquetbol un equipo anotó un total de 55 canastas, obteniendo 125 puntos.
¿Cuántos tiros de campo (2 puntos) y triples realizaron?
Resolución:
Se nombrará “X” a las canastas encestadas de 2 puntos y “Y” a las de 3 puntos.
La primera ecuación queda planteada con respecto a las canastas encestadas.
La segunda ecuación queda planteada con respecto al número de puntos que hizo el equipo.
¿Cuántos puntos fueron de 2?
¿Cuántos puntos fueron de 3?
El sistema de dos ecuaciones lineales con dos incógnitas queda así:
Paso 1. Se despeja la incógnita “x” de la primera ecuación:

Paso 2. Se despeja la incógnita “????” de la segunda ecuación:
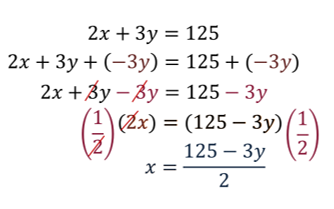
Paso 3. Se igualan las ecuaciones despejadas:
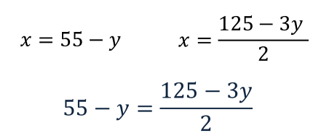
Paso 4. Se resuelve la ecuación de primer grado obtenida en el paso 3, para encontrar el valor de la incógnita “y”.
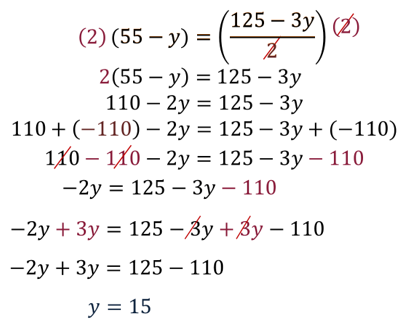
Paso 5. Se sustituye el valor numérico de la incógnita “y=15” en la primera ecuación despejada:
La solución del sistema es:
Por lo tanto, el equipo metió 40 canastas de 2 puntos y 15 canastas de 3 puntos.
Analiza el siguiente ejercicio para profundizar en el tema y aplicar lo aprendido.
Ejercicio 2
Calcular el valor de las incógnitas “x” y “y” del siguiente sistema de ecuaciones lineales con dos incógnitas.
Recuerda que, para resolver el sistema de ecuaciones con el método de igualación, debes realizar una serie de pasos.
Paso 1. Se despeja la incógnita “x” de la primera ecuación.

Para poder cancelar el coeficiente de la literal “4x”, se usa el inverso multiplicativo, en este caso se multiplicó por un cuarto (1/4) en ambos miembros de la ecuación.
Paso 2. Se despeja la incógnita “x” de la segunda ecuación.
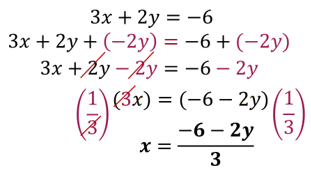
Paso 3. Se igualan las ecuaciones despejadas.

Paso 4. Se resuelve la ecuación de primer grado, para encontrar el valor de la incógnita “y”.
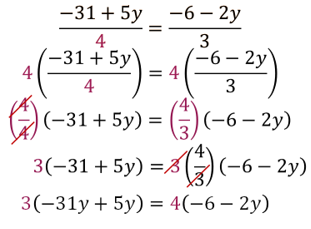
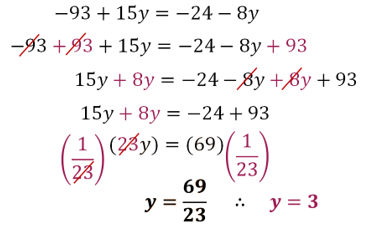
Por lo tanto:
“y” es igual a sesenta y nueve entre veintitrés, es decir, el valor es tres.
Paso 5. Se sustituye el valor numérico de la literal “y”, y=3 en la primera ecuación despejada.

El valor de la incógnita “x” es, menos cuatro.
La solución del sistema es:
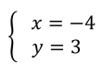
Comprobación. Se sustituye el valor numérico de las incógnitas “x” y de “y” en las ecuaciones 1 y 2.

Con lo anterior, queda comprobado que los valores numéricos de las literales “x” y “y” satisfacen la igualdad.
Entonces: “x” es igual a -4, y “y” es igual a 3.
Hasta este momento has estudiado dos métodos para la resolución de problemas planteando y resolviendo un sistema de ecuaciones lineales con dos incógnitas: El método gráfico y el método algebraico de igualación.
En la siguiente sesión resolverás problemas utilizando el método algebraico de sustitución.
El Reto de Hoy:
Resuelve el siguiente ejercicio mediante el planteamiento de un sistema formado con dos ecuaciones lineales con dos incógnitas, utilizando el método de igualación.
Ejercicio 3
Calcular el valor de las incógnitas “x” y “y” del siguiente sistema de ecuaciones.
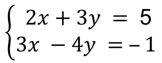


No hay comentarios.:
Publicar un comentario