PRIMEROS AÑOS
23/10/2020
Gráficas de variación
Aprendizaje esperado: Analiza y compara situaciones de variación lineal a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con estos tipos de variación.
Énfasis: Comparar gráficas de variación lineal. Comparar tipos de variación lineal y la razón de cambio. Identificar la pendiente de la recta y su relación con la razón de cambio.
¿Qué vamos a aprender?
En esta sesión retomarás lo que aprendiste sobre el significado de variación lineal y su representación tabular, trabajarás con gráficas que representan una variación lineal y verás su utilidad en la toma de decisiones, así como para predecir y estudiar acontecimientos.
Ten presentes todos los conocimientos que ya has adquirido para poder adueñarte de los nuevos conceptos que el día de hoy te presentaremos.
¿Qué hacemos?
En esta lección elaborarás algunas gráficas. Seguramente las has utilizado o ha escuchado hablar de ellas. Existen distintos tipos, entre los cuales se encuentran la gráfica de barras, muchas veces utilizada para representar la frecuencia con la que se presenta un dato o variable, por ejemplo:
Las calificaciones obtenidas en la asignatura de Ciencias o de Historia en un grupo de alumnos.
O bien la gráfica circular, que se usa para representar una proporción o un porcentaje, por ejemplo:

Los resultados de una encuesta que se realiza en cierta población de alumnos de una escuela, sobre su color favorito.
Existen otros tipos de gráficas, como la de dispersión o el histograma.
Las gráficas son de gran utilidad. En esta lección analizarás las que se construyen en el plano cartesiano. El plano cartesiano está conformado por dos rectas numéricas perpendiculares entre sí y el punto donde se intersecan se llama origen. Al eje línea horizontal se le conoce como el eje de las abscisas o eje de las “x” y al eje vertical, como eje de las ordenadas o eje de las “y” Así que, para ubicar una coordenada, primero ubicamos el número que representa a “x” las abscisas, y posteriormente el que representa a “y” las ordenadas.
Por ejemplo, la coordenada (4,3) queda de la siguiente manera: ubicamos primero el 4 en el eje de las abscisas, a continuación, el 3 en el eje de las ordenadas, observamos el punto de intersección y éste será el punto de la coordenada (4,3)
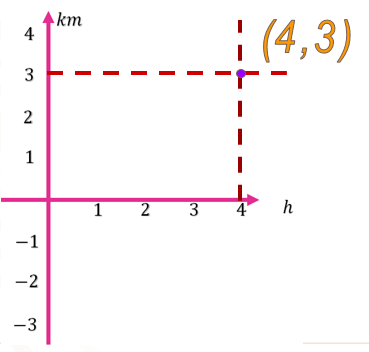
Este tipo de gráficos nos ofrecen una gran posibilidad de entender fenómenos de variación. Y para comprenderlo mejor, retomaremos lo que estudiaste durante las sesiones anteriores. Comenzaremos con las tablas de variación lineal que ya trabajaste, específicamente las que representan la relación entre el tiempo y la carga de un teléfono celular.
Analizaste una tabla que muestra que, conforme los minutos aumentan, el porcentaje de carga también aumenta; identificaste que la variable dependiente “y” corresponde al porcentaje de carga, y que la variable independiente “x” representa los minutos. Tomaste en cuenta una condición inicial, ya que el celular comienza a cargarse a partir de 15% del total de la capacidad de carga, así que la expresión algebraica que se obtuvo fue: y = (1.7) (x) + 15

Para encontrar los minutos que tarda en llegar la carga a 100%, se usaron los valores 25 y 38 Hasta aquí aún no tenemos los minutos que tarda en cargarse completamente el celular, ya que a los 25 minutos se obtuvo un porcentaje de 57.5 y a los 38 se tiene un total de 79.6%

Continuemos llenando la tabla. Sustituiremos en la expresión algebraica los valores numéricos y calcularemos la carga total a los 45 minutos de haber conectado el celular a la corriente.
Al multiplicar (1.7) (45) su producto es 76.5 posteriormente sumamos 15 y así obtenemos 91.5 El resultado representa 91.5% de la carga total.
|
|
|
|
Podemos registrar ambos valores en la tabla.

Ahora realizaremos el cálculo con 50 minutos. Multiplicamos 1.7 por 50 que es igual a 85 a este número le sumamos 15 que corresponde a la condición inicial, y al fin hemos obtenido 100 que representa 100% de carga.
|
|
|
|
Esto quiere decir que, para que el celular se cargue completamente, debemos mantenerlo conectado a la corriente eléctrica durante 50 minutos.
Ahora tenemos nuestra tabla completa. Observemos: Comenzamos con un valor de 5 minutos en la medida del tiempo, que corresponde a 23.5% de batería, y va aumentando, de manera que llegamos hasta los 50 minutos con una carga de 100%.

Ahora con los datos de la tabla puedes elaborar una gráfica, para eso irás ubicando cada uno de los puntos de la tabla en el plano cartesiano, observa el siguiente video hasta el minuto 02:34, que te ayudará con los pasos a seguir para realizar la gráfica de este problema.
- Gráfica (Celular)
¿Sabías que uno de los tramos carreteros más largos del mundo, en línea recta, se encuentra en México y está en Baja California Sur?
Este tramo forma parte de la Carretera Transpeninsular de Baja California y abarca mayormente el municipio de Comondú y una pequeña parte del municipio de La Paz; mide aproximadamente 168 kilómetros de largo.
Una persona de nombre Lalo que radica justo a las afueras de Ciudad Constitución, cierto día realizó un viaje por esta ruta con su familia y dos amigos más, viaje en el que decidieron encontrarse en cierto punto para desayunar.
Ubiquémonos de nuevo en el mapa; imagina un plano cartesiano sobre él.
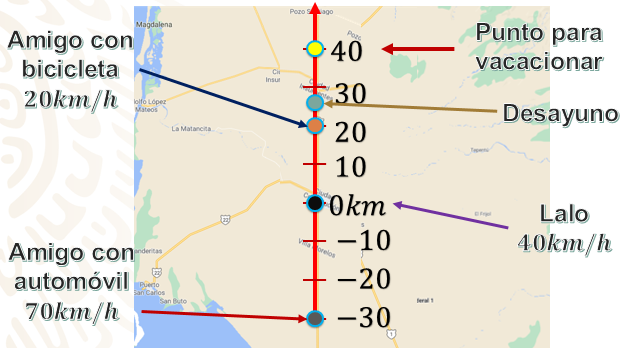
Toma en cuenta que al punto de partida de Lalo le llamaremos punto de origen, o bien “punto cero”, ya que es el protagonista de nuestro planteamiento. Su destino era hacia La Purísima, 40 kilómetros al norte. Todos salieron a la misma hora desde donde estaban.
El primer vehículo es un automóvil que viaja a una velocidad constante de 40 km/h, el segundo vehículo es una bicicleta que recorre una distancia de 20 km/h y el tercer vehículo es otro auto que viaja a 70 km/h.
Observa el siguiente video del minuto: 00:20 al 01:04 que ilustra el recorrido que realizaron.
- Viaje de Lalo
Un aspecto interesante que se plantea en el video es que el punto para desayunar se encuentra justo 25 km más allá de la casa de Lalo. Encuentra el orden en que llegan a dicho lugar.
Para analizar con más detenimiento la información, anota en tu cuaderno las siguientes preguntas:
¿De qué manera puedes conocer el orden en que llegó cada vehículo?
¿Por qué el primero en llegar es el amigo de Lalo, que va en bicicleta, si su velocidad es menor?
Para contestar la pregunta uno, observa la siguiente imagen:
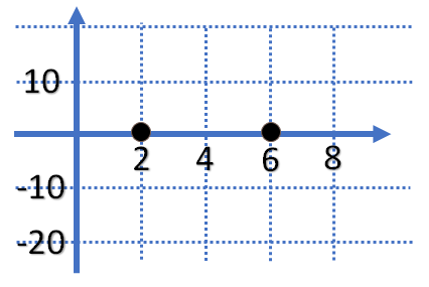
El eje horizontal corresponde al tiempo, quiere decir que entre más avanzado o lejos esté el punto del 0, mayor será el tiempo que ha pasado. Atención: señalaremos 2 horas, ahora 6 horas; como observas, este último punto se encuentra mucho más alejado del 0, por lo que deducimos que entre más tiempo tarde en desplazarse el vehículo, su ubicación con respecto al origen será cada vez más a la derecha.
El siguiente video del minuto: 02:40 al 03:20te ayudará a ilustrar el orden en que llegaron los viajantes:
- Viaje de Lalo
Así que, el vehículo que tarda menor cantidad de tiempo en llegar es la bicicleta, enseguida llega el auto que maneja Lalo y posteriormente llegó el otro amigo que, al igual que Lalo, viajó en auto.
Bien, ya confirmamos que la manera de estudiar la gráfica con respecto al tiempo es analizando el eje que lo representa, es decir, el eje horizontal, o bien el eje “x”; asimismo, podemos estudiar el desplazamiento de cada vehículo si prestamos atención al eje vertical, o bien al eje “y” es decir:
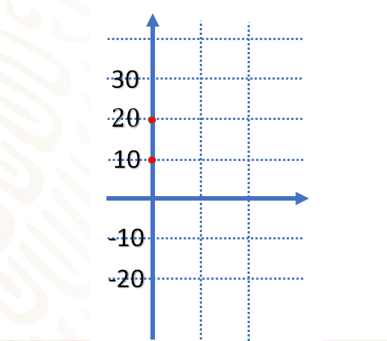
Entre más alejado se encuentre el punto, mayor será la distancia a la que se encuentre el vehículo respecto al origen. Observa que el primer punto está sólo a 10 km y el segundo está a 20 km, y lo vemos más arriba, o bien más lejos del 0. Con esto podemos responder la pregunta dos: ¿por qué el primero en llegar es el amigo de Lalo, que va en bicicleta, si su velocidad es menor?
- Viaje de Lalo
Del minuto: 01:37 al 02:07
Como notaste desde un inicio, el amigo que va en bicicleta ya tiene 20 km del trayecto adelantados, por lo que únicamente le faltan 5 km para llegar al punto donde tomarán su desayuno. Por otro lado, la velocidad a la que viajan las otras dos personas no es suficiente para llegar con anticipación.
Otra situación similar es la caminata que realizaron tres personas en un circuito. Un observador, que contaba con cronómetro y que conoce las distancias en el recorrido, tomó el registro de sus desplazamientos. Analicemos la información mediante sus respectivas gráficas. Anota el registro que realizó el observador.
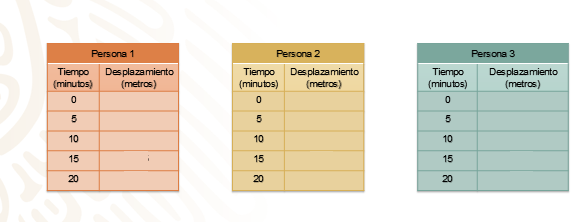
Presta atención a que el espectador tomó el registro a 0, 5, 10, 15 y 20 minutos de haber iniciado el registro. El desplazamiento registrado de la persona 1 fue de 0, 7.5, 15, 22.5, y 30 metros, respectivamente. La persona 2 registró 10, 20, 30, 30 y 40 metros. La tercera persona, 5, 10, 15, 20 y 25 metros.
Con los registros del espectador, vamos a elaborar las tres gráficas correspondientes en un plano cartesiano.
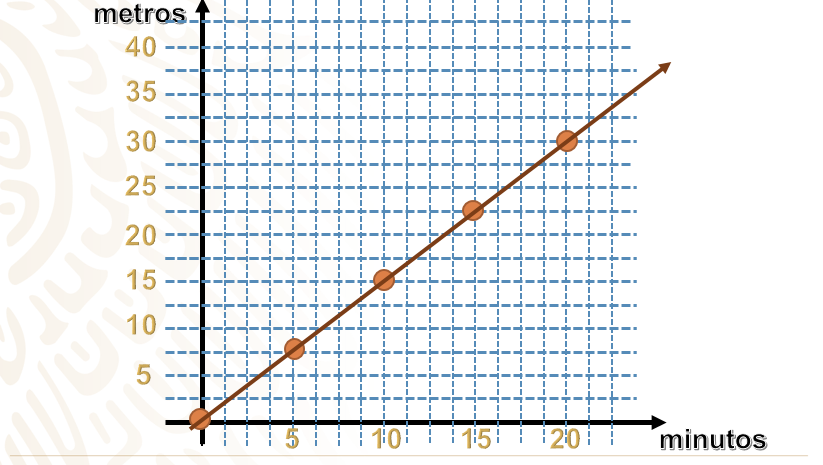
Localizamos las coordenadas de la persona 1. Sigue el procedimiento: primero se ubica la abscisa y después la ordenada:
(0,0), (5,7.5), (10,15), (15,22.5) y (20,30)
Ahora unimos los puntos de las coordenadas. Atención a que, al momento en que el observador toma su registro, esta persona no había avanzado un solo metro en el recorrido, por eso inicia en el origen.
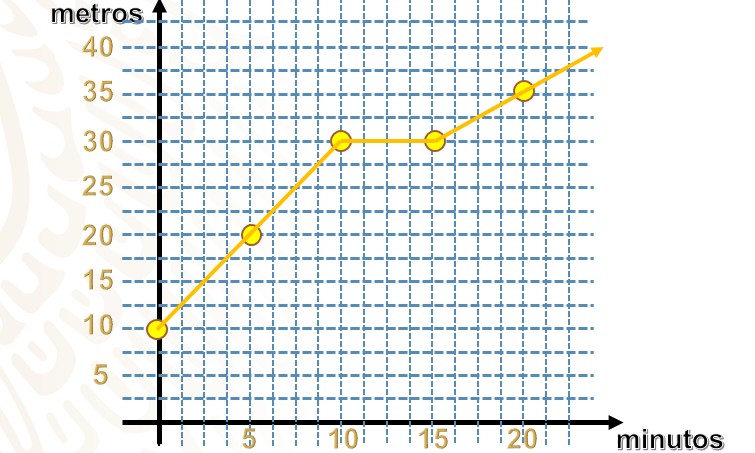
Para la persona 2, las coordenadas son:
(0,10), (5,20), (10,30), (15,30) y (20,40)
Ahora unimos los puntos y observamos una cuestión muy particular: esta persona ya tenía 10 metros avanzados al iniciar su registro, además de que su gráfica no es como las que has visto.
Terminemos de graficar para estudiar con detenimiento estas situaciones. Las coordenadas que corresponden al desplazamiento de la persona 3 son:
(0,5), (5,10), (10,15), (15,20) y (20,25)
Y esta persona, ya tiene 5 metros recorridos al momento en que se inicia la observación.
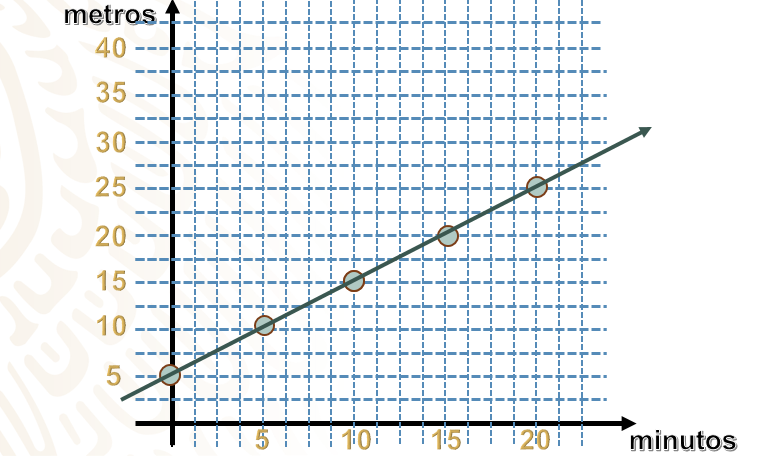
¿Qué diferencia observas entre las gráficas? Toma tu cuaderno y anota estas preguntas que te ayudarán a entender mejor la situación.
¿El trayecto recorrido por la persona 2 fue realizado a un desplazamiento constante?
Según la gráfica que representa el trayecto de la persona 2, ¿qué sucede entre los minutos 10 y 15?
Como puedes observar, el desplazamiento de la persona 2 fue constante del minuto 0 al 10; después del minuto 15, ¿su velocidad fue mayor o menor con respecto al inicio?
¿Podrías predecir cuál será su desplazamiento para el minuto 30?
Contestemos las preguntas:
La gráfica que representa el recorrido que realiza la persona 2 es diferente al de las personas 1 y 3, ya que no determina una línea recta. Por lo tanto, visualmente podemos determinar que el trayecto recorrido por la persona 2 no fue realizado a una velocidad constante, ya que, dando respuesta a la tercera pregunta, podemos observar que entre el minuto 10 y 15 no hay un desplazamiento de la persona, el segmento de recta se mantiene horizontal; esto quiere decir que sigue existiendo un incremento en la unidad del tiempo, pero no en la unidad que corresponde a los metros.
Ahora realicemos algunos cálculos matemáticos para dar respuesta a la última pregunta, encontrando la razón de cambio. Toma nota, seguiremos el procedimiento del video.
Usaremos la primera coordenada, que es (0,10), y la tercera (10,30). Con respecto a los valores de “y” el valor absoluto de su diferencia es 20, y en lo que se refiere a los valores absolutos de “x” la diferencia es de 10; calculamos la división y/x y obtenemos que la razón de cambio es 2
Analicemos lo que sucede entre los minutos 10 al 15. Entre la tercera y cuarta coordenada el desplazamiento fue nulo, ya que no se incrementó la distancia recorrida, pero el tiempo sí avanzó 5 minutos más, obteniendo así, una razón de 0
Por otro lado, la cuarta coordenada es (15,30) y la quinta (20,35), el valor absoluto de la diferencia entre los valores del eje de las ordenadas es 5 y la diferencia entre los valores del eje de las abscisas también es 5 por lo que su razón de crecimiento es de 1
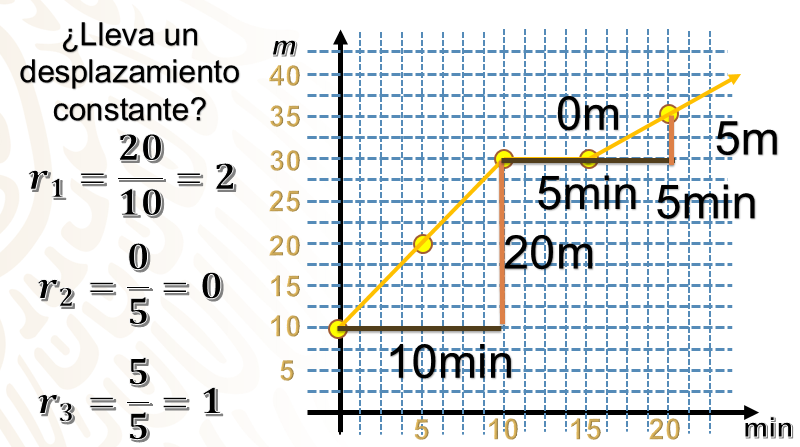
Queda claro que tenemos distintas razones de cambio a lo largo de la gráfica, por lo tanto, ésta no representa una variación lineal, ya que para que cumpla con esta característica, su razón de cambio tendría que ser la misma a lo largo de toda la gráfica.
En ese lapso entre los minutos 10 y 15 La persona pudo haberse detenido a tomar un respiro en su caminata.
Ahora, como pudiste ver, su razón de cambio en el tramo final es menor que en el inicial, lo que nos indica que la persona regresó a hacer su caminata, pero con una velocidad menor.
Con esto damos por concluida la respuesta a la segunda pregunta: ¿qué sucedió entre el minuto 10 y 15? probablemente, se detuvo a tomar agua.
La última pregunta fue: ¿podrías predecir cuál será su desplazamiento para el minuto 30?
No podríamos saberlo, ya que no ha demostrado consistencia en su desplazamiento y no sabemos si se volverá a detener o continuará con la razón de cambio que lleva al minuto 20 Pero, ¿qué piensas?
Para terminar el análisis de esta situación, responde las siguientes preguntas:
- ¿Puedes determinar si con las personas 1 y 3 hay variación lineal?
- ¿Cuál es la razón de cambio de las dos personas?
- ¿Cuál será su desplazamiento a los 30 minutos?
Como lo hiciste anteriormente, analicemos la gráfica de la persona 1 por separado.
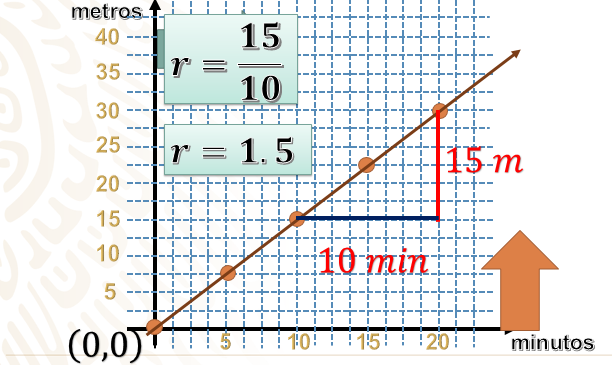
Observa que podemos trazar fácilmente una recta que pase sobre todas las coordenadas, por lo que esto nos indica que es una variación lineal, muy en particular, una variación de proporción directa.
Aumenta el conjunto independiente con la misma razón que el dependiente, y lo más importante en la proporción directa es que el inicio de los datos siempre será en el origen, es decir, 0 en la abscisa y 0 en la ordenada, lo que no necesariamente siempre sucede en el caso de la variación lineal.
Calculemos su razón de cambio:
Elegimos dos coordenadas y contamos la distancia que los separa, primero en las ordenadas, que es 15 m. Después contamos la distancia entre ambas coordenadas en las abscisas, que es 20 minutos. Establecemos la razón y obtenemos el cociente de la diferencia de las ordenadas entre la diferencia de las abscisas, lo que representa 15 entre 10, que es 1.5
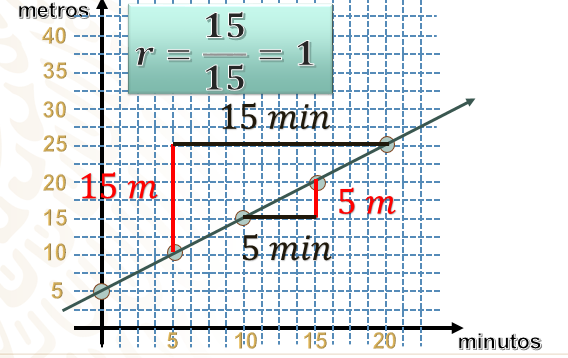
Ahora veamos la gráfica de la tercera persona. Observamos que muy fácilmente se pueden unir con una recta todas las coordenadas encontradas. Por esta razón, podemos determinar que es una variación lineal. A diferencia de la gráfica anterior, ésta no pasa por el origen, lo que nos dice que no es una gráfica de proporcionalidad directa, aunque sí podemos determinar su razón de cambio eligiendo cualquier par de coordenadas y obteniendo su razón.
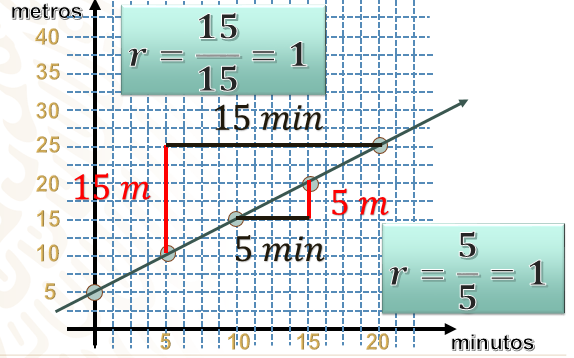
Entre estas coordenadas (10,10) y (20,20) su razón de cambio será de 5 entre 5, que es 1. No importa el par de coordenadas que elijas, la razón será siempre la misma. Observa: si elegimos las coordenadas (5,10) y (20,25) la diferencia es de 15 tanto en las abscisas como en las ordenadas, por lo que su razón de cambio también es de 1
La línea recta de la gráfica de proporción directa necesariamente pasa por el origen. La línea recta de una variación lineal no necesariamente pasa por el origen. Ahora, utilizando la razón de cambio, podemos responder la última pregunta: ¿cuál será su distancia a los 30 minutos?
Analicemos:
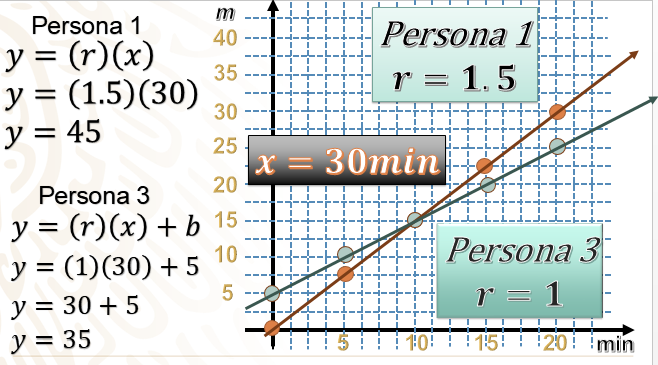
Hay que tener claro que nuestra variable independiente es el tiempo x = 30 y nuestra variable dependiente “y” es desconocida en este momento.
Para la persona 1: Su razón de cambio es 1.5 y el tiempo a obtener es 30. Debemos multiplicar los datos y así obtenemos 45 lo que quiere decir que la primera persona avanza 45 metros.
Para la persona 3 Su razón de cambio es de 1 y el tiempo a obtener es de 30 minutos. Al efectuar la multiplicación de ambos valores, el resultado es 30 pero en esta ocasión hay que agregarle 5 metros debido a que en el momento que se comenzó con el registro, esta persona ya se encontraba 5 metros más adelante del punto de partida en la pista. Así obtenemos que 30 + 5 = 35 por lo que la persona 3 avanza un total de 35 metros después de 30 minutos.
Ya tenemos la respuesta a las tres preguntas con las que comenzamos este análisis. ¿Has notado que la persona 1 tenía un desplazamiento mayor al de la persona 3? Esto lo sabemos por su razón de cambio, 1.5 es mayor que 1, pero sólo al ver la gráfica lo podemos saber sin la necesidad de calcular la razón de cambio.
Estamos hablando de la pendiente, o bien la inclinación. La recta que se forma por una variación lineal tiene una relación muy estrecha entre el valor de la razón y su ángulo respecto al eje de las abscisas. Es un tema muy interesante, pero requiere de mucho más tiempo y conocimientos avanzados. Por el momento y por la simple observación de los ejemplos que revisaste en la sesión de hoy, podemos tener esta conclusión.
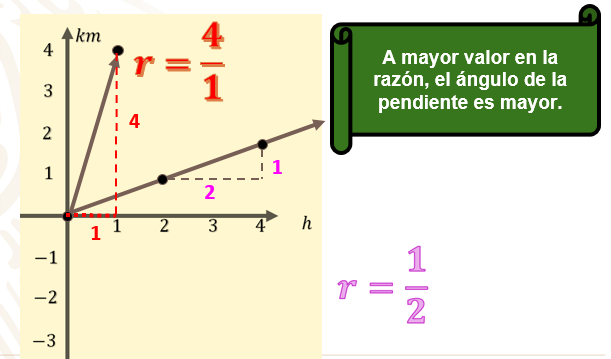
Como te has dado cuenta, todas las gráficas presentadas tienen características similares:
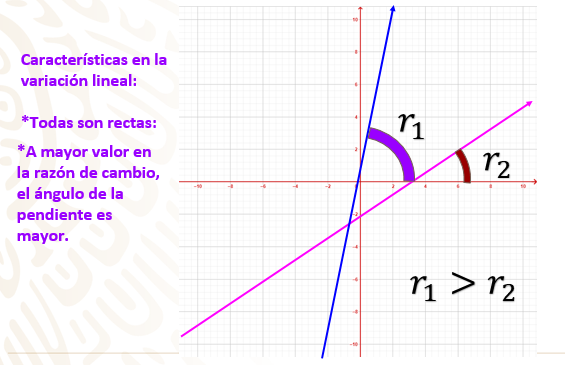
Al describir la variación en cada una de las situaciones presentadas, obtenemos una línea recta, de ahí que reciba el nombre de variación lineal.
A mayor valor en la razón, el ángulo de la recta con respeto al eje de las abscisas es mayor.

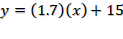
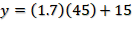
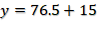
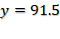
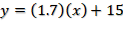
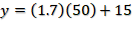
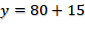
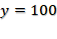

No hay comentarios.:
Publicar un comentario