tercero años
07/10/2020
Figuras y simetría
Aprendizaje esperado: Explica el tipo de transformación (reflexión, rotación o traslación) que se aplica a una figura para obtener la figura transformada. Identifica las propiedades que se conservan.
Énfasis: Construir figuras congruentes o semejantes (triángulos, cuadrados y rectángulos) y analizar sus propiedades.
¿Qué vamos a aprender?
Explorarás las propiedades que se conservan de las figuras simétricas.
Anota en tu libreta las dudas, inquietudes o dificultades que surjan al realizar las actividades de esta sesión, así como sus conclusiones. Éstas las puedes resolver con el apoyo de tu profesor y también te puedes apoyar con tu libro de texto o al reflexionar en torno a las actividades que se realizarán.
Un alumno llamado Rubén, que saliendo de la secundaria y mientras cursaba la preparatoria, se dedicó a tomar cursos de fotografía, le gusta experimentar con espejos y de vez en cuando manda algunas fotos para mostrar su trabajo. Esta es unas de sus fotografías ¿qué te parece?, ¿te gusta?

mediciones, el reflejo no tiene las mismas medidas que la figura, lo que indica que estos objetos no son equidistantes.
Selecciona otro objeto, en este caso será el poste de luz que se ve como una letra “T”, realiza las mediciones.
Los resultados son: poste de luz 1 cm y el reflejo de éste mide 0.6 cm, partiendo del eje de simetría, lo que indica que la distancia de la T del poste no es igual que la de la T del poste del reflejo. Esta “figura” tampoco es equidistante.
Por tanto, como las medidas entre los objetos a partir del eje de simetría no son las mismas, no puedes considerar que el reflejo en la fotografía de Rubén es una imagen simétrica.
¿Qué hacemos?
Analiza las características de las siguientes imágenes, ¿qué notas?

Lo primero que se nota es que son 2 imágenes muy conocidas en todo México, tenemos el palacio de Bellas Artes y una representación del dios mexica Xiuhtecuhtli.
Si trazas una línea vertical, a la mitad de cada imagen y la cortas, obtienes dos imágenes iguales, puedes observar el resultado del experimento.
El corte que se realiza a las imágenes podría considerarse como eje de simetría, porque las divide por la mitad.
¿Será que las imágenes son simétricas?
No necesariamente son simétricas las imágenes aun cuando se puedan dividir por la mitad. Por ejemplo, el dios Xiuhtecuhtli no tiene los brazos del todo simétricos, aun cuando se divida por la mitad no es una figura simétrica.
En comparación con el palacio de Bellas Artes, la línea sí lo divide por la mitad y sus esculturas están a la misma distancia de la línea divisoria, por lo tanto, podríamos decir que el palacio de Bellas Artes es simétrico.
¿Recuerdas alguna imagen, foto donde se pueda partir por la mitad con un doblez como lo visto anteriormente ya sea en libros, revistas? Si no es así, como actividad te proponemos buscar imágenes en libros, revistas, algunos monumentos de su estado o municipio y, traza su eje de simetría mediante un doblez que te permita saber si hay simetría.
Comparte con tus compañeros y profesor tus observaciones cuando tengas oportunidad.
Los resultados de las imágenes anteriores son un acercamiento que tiene que ver con el tema de las propiedades de las figuras simétricas.
Observa las siguientes actividades para descubrir las propiedades que conservan las figuras simétricas.


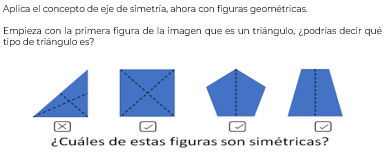
Es un triángulo rectángulo.
Ahora traza un segmento que lo divida y observa si las dos figuras que se forman al cortarla son iguales.
Puedes ver que no es así, porque el trazo no fue un eje de simetría, pero no debes rendirte, trazarás un segundo segmento para ver si lo logras esta vez.
Cómo puedes observar, la figura no se pudo dividir en dos partes iguales, por lo que puedes decir que esta primera figura no tiene eje de simetría. No importa cómo traces líneas que dividan esta figura, no podrás obtener dos imágenes iguales, donde una sea reflejo de la otra.
Sin embargo, recuerda que hay varios tipos de triángulos y el hecho de que este triángulo rectángulo no sea simétrico no quiere decir que los demás tipos tampoco lo sean.
¿Puedes investigar qué tipo de triángulo si tiene uno o varios ejes de simetría? consúltalo con tu profesor cuando tengas oportunidad.
Observa qué ocurre con la siguiente figura que es un cuadrado, traza un segmento de recta que vaya de un vértice a otro opuesto, es decir, estas trazando una diagonal del cuadrado.
Analizando el corte, se formaron 2 triángulos semejantes, porque ambos tienen sus ángulos y lados de la misma medida, esto quiere decir que el cuadrado si tiene eje de simetría, es más traza otra diagonal para comprobar qué ocurre.
Cómo puedes ver es posible trazar más de un eje de simetría en algunas figuras, te sugerimos descubrir si hay más ejes de simetría en el cuadrado y comentarlo con tus compañeros de clase y tu profesor cuando tengas oportunidad.
Puedes marcar entonces que esta figura si tiene eje de simetría, de hecho, tiene más de un eje de simetría.
Prueba ahora con la siguiente figura, es un pentágono regular, traza la mediatriz que va desde la base al vértice superior y observa qué ocurre.
Puedes darse cuenta de que se genera un efecto similar al de las figuras que observaste al inicio, es un efecto de “espejo”, puedes decir sin temor a equivocarte que esta figura es simétrica y que haz trazado correctamente su eje de simetría.
Observa ahora la siguiente figura, por sus características es un trapecio, traza ahora la mediatriz de la base, como se muestra a continuación, y observa que sucede.
Pudiste observar que una vez más trazaste el eje de simetría de la figura.
¿Podrías trazar más ejes de simetría a las figuras que ya marcaste cómo simétricas?
Observa cómo se traza una figura simétrica y cuáles son las propiedades que debe de conservar.
Antes de continuar observa algunos conceptos:
Las rectas perpendiculares son aquellas que al interceptarse forman ángulos de 90°.
Además, para indicar el simétrico de un vértice se utiliza la misma letra, pero con un apostrofo, con el fin de diferenciar la figura original de la simétrica, y se lee “A prima”.




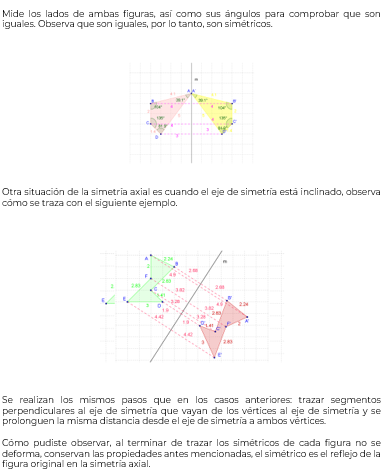

Sigues el mismo procedimiento con los demás vértices para tener todos y cada uno. Una vez que traces todos los vértices sólo falta unirlos en el mismo orden en que fuiste trazándolos y así formarás la figura simétrica.
Si lo analizamos, los vértices de ambas figuras están a la misma distancia, pero del punto de simetría en lugar de un eje de simetría. por ello la figura simétrica resultante está invertida.
Cómo pudiste observar, la simetría no es sólo un reflejo o sólo la división por la mitad de una imagen o figura, debe de tener características muy particulares, ¿te acuerdas cuáles son?
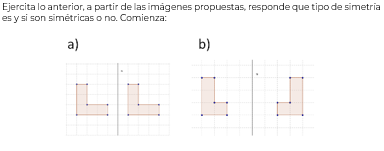
¿Presenta Simetría axial?
- No, porque debería de parecer como si fuera un reflejo.
- Si son, por que están a la misma distancia del eje de simetría, una es el reflejo de otra.
¿Presenta Simetría axial?
- Si son simétricas, por estar a la misma distancia del eje de simetría, sus lados son iguales y sus ángulos también.
- No son simétricas, porque no están a la misma distancia del eje de simetría, aun cuando es la misma figura.
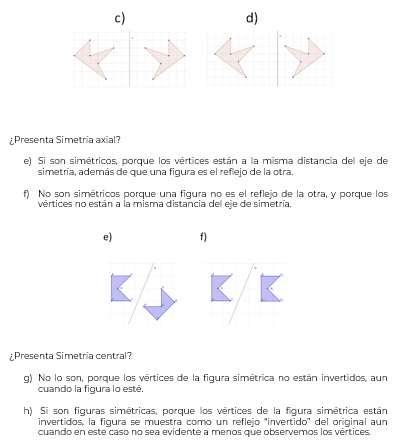

Resumiendo, para que una figura se considere simétrica de otra con respecto a un eje de simetría, debe de conservar:
1. Los vertices de ambas figuras deben de estar a la misma distancia del eje de simetría.
2. Los ángulos deben de tener la misma medida; y, por último,
3. La longitud de sus lados debe ser la misma.
El Reto de Hoy:
Para reforzar los conocimientos observa las siguientes preguntas:





No hay comentarios.:
Publicar un comentario